Z-N法整定PID参数：最佳实践、限制与挑战的专家见解


# 摘要
本文综述了Ziegler-Nichols (Z-N) 方法在整定PID控制器参数的应用，从理论基础到实践应用再到进阶实践进行了全面探讨。文章首先介绍了PID控制器的基本概念以及Z-N法的理论起源和应用原理，详细解释了整定步骤并分析了不同调整规则。接着，文章探讨了Z-N法在工业控制系统中的实际应用，包括流程和温度控制系统的案例分析，并讨论了常见问题的诊断与解决策略。此外，本文也对Z-N法的局限性进行了分析，并提出了改进策略。最后，文章展望了Z-N法的未来发展方向，包括与其他现代控制技术的融合和人工智能的应用前景。本文旨在为控制工程师提供Z-N法整定PID参数的深入理解和实际应用指南。

# 关键字
Ziegler-Nichols方法；PID控制器；整定参数；工业控制系统；自适应控制；人工智能优化

参考资源链接：[Z-N法整定PID参数经验分享](https://wenku.csdn.net/doc/6412b793be7fbd1778d4acb6?spm=1055.2635.3001.10343)
# 1. Z-N法整定PID参数概述

在自动控制领域，PID控制器因其简单有效而被广泛应用。PID控制器通过比例（P）、积分（I）、微分（D）三种控制动作对系统进行调整，以达到期望的控制效果。然而，PID参数的选取直接影响到控制器的性能，合理的参数设置对于控制系统来说至关重要。

Ziegler-Nichols（Z-N）方法是最早提出且最为著名的PID参数整定技术之一，其核心思想是通过一系列的实验获取过程动态特性，进而计算出一组适合特定系统的PID参数。Z-N法操作简便，易于理解和实施，成为工业界和学术界广为应用的整定方法。

尽管Z-N法在众多领域中取得了成功，但它也存在一定的局限性。例如，它在处理非线性系统、时变系统以及具有复杂动态特性的系统时可能会遇到困难。因此，在实际应用中，工程师需结合具体系统的特性，对Z-N法进行适当的调整和优化。本章将概述Z-N法整定PID参数的基本概念和使用场景，为读者进一步深入理解其理论基础与应用原理打下基础。

# 2. Z-N法理论基础与应用原理

## 2.1 PID控制器基本概念

### 2.1.1 控制器的作用与目标
PID控制器是一种广泛应用于工业控制系统的反馈控制器，其作用是根据系统的当前状态来调整控制输入，以使得输出能够尽可能快地达到并维持在期望的设定值。PID控制器的主要目标是减少系统误差，增强系统的稳定性和抗干扰能力，提高系统的动态和静态性能。

### 2.1.2 PID参数的定义与影响
PID控制器包含三个主要的参数：比例（P）、积分（I）和微分（D），这三个参数对系统的动态响应有着决定性的影响。
- **比例（P）参数**：影响系统的响应速度和稳态误差，较大的P值可以提高系统的响应速度，但同时可能会引入较大的超调。
- **积分（I）参数**：用于消除稳态误差，如果系统对稳态精度有较高要求，则需要增加积分项的权重。
- **微分（D）参数**：通过预测系统的未来趋势，对系统的快速动作进行抑制，有助于减小超调并提高响应速度。

## 2.2 Ziegler-Nichols方法的起源与发展

### 2.2.1 方法的提出背景与理论依据
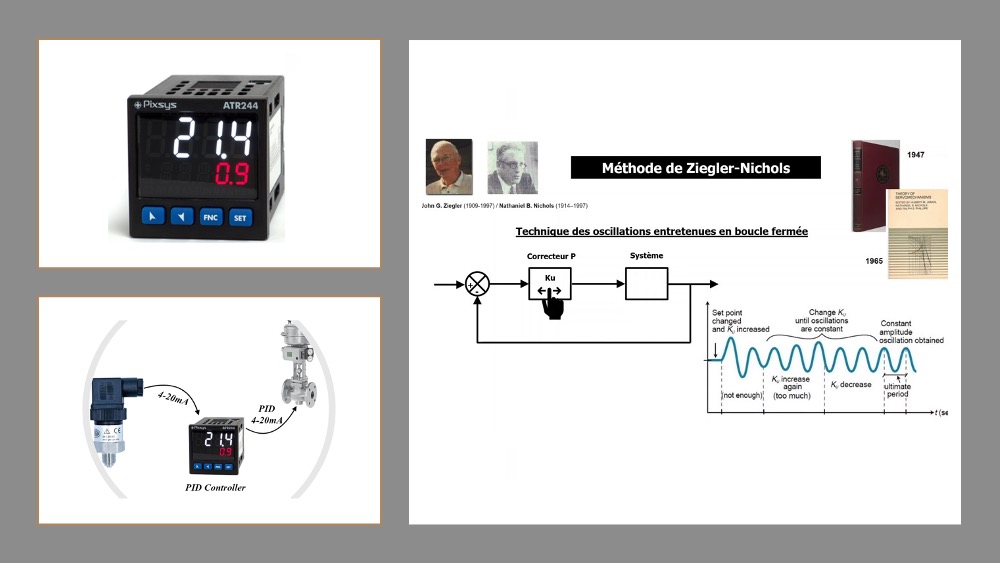
Ziegler-Nichols（Z-N）方法是一种历史久远且广泛使用的PID参数整定技术。该方法最早由John G. Ziegler和Nathaniel B. Nichols于1942年提出，它的理论依据是基于对开环和闭环系统行为的实验观察和分析。Z-N方法通过实验确定临界比例带宽和临界振荡周期，以计算得到一组粗略的PID参数。

### 2.2.2 不同Z-N调整规则的对比分析
Z-N方法提出了两套调整规则：Ziegler-Nichols开环调整规则和闭环调整规则。
- **Ziegler-Nichols开环调整规则**：适用于开环稳定系统，通过开环测试确定系统响应曲线，进而计算出PID参数。
- **Ziegler-Nichols闭环调整规则**：适用于闭环稳定系统，通过调整系统的闭环特性来确定PID参数。

## 2.3 Z-N法整定步骤详解

### 2.3.1 开环测试与临界增益确定
要使用Z-N法进行PID参数的整定，首先需要进行开环测试。在这一步骤中，系统以手动模式运行，对控制输入进行逐步增加直到系统输出开始持续振荡。此时的增益称为临界增益（Ku），对应的振荡周期称为临界周期（Tu）。

### 2.3.2 依据临界周期设置PID参数
临界增益和临界周期被确定后，可以根据Z-N方法提供的经验公式来设置PID参数。以下是开环法的参数计算公式：

P = 0.6 * Ku
I = 2 * P / Tu
D = P * Tu / 8

通过上述公式，我们可以计算出初步的PID参数值，进而将控制器调整至手动模式并应用这些参数。通过细微的调整，可使系统达到理想的工作状态。

在下一章节中，我们将深入了解Z-N法在实际工业控制系统中的应用，并通过具体案例分析来展示Z-N法的优势与挑战。

# 3. Z-N法整定PID参数的实践应用

Ziegler-Nichols（Z-N）方法作为经典的PID参数整定技术，广泛应用于工业控制系统中。它提供了一种系统化、标准化的方式来调整PID控制器参数，以实现系统性能的最优化。在这一章中，我们将深入探讨Z-N法在实际工业环境中的应用，同时分析常见的问题及其解决策略，并与其他整定技术进行对比。

## 3.1 工业控制系统中的Z-N法应用

### 3.1.1 流程控制系统的PID参数调整

流程控制系统是工业自动化的基础，它涉及液体、气体或固体材料的流动和处理。PID控制器在其中扮演着至关重要的角色，它确保了流程的稳定运行和产品质量的一致性。使用Z-N法进行PID参数调整，能够使控制系统快速响应给定的动态变化，同时减少超调和振荡，从而提高整个系统的性能。

调整流程控制系统中的PID参数通常遵循以下步骤：

1. 从一个安全的参数设置开始，通常采用较保守的P控制。
2. 进行开环测试，逐渐增加控制器的输出直到系统开始振荡。
3. 记录下振荡发生时的比例增益（临界增益Ku）和周期（临界周期Pu）。
4. 根据Z-N提供的公式，计算PID控制器的比例、积分和微分参数。

# 以下是根据Z-N公式调整PID参数的一个示例代码
# 设置临界增益和周期
Ku = 10.0
Pu = 20.0

# 计算PID参数
Kp = 0.6 * Ku
Ki = 2 * Kp / Pu
Kd = Kp * Pu / 8

### 3.1.2 温度控制系统的案例分析

温度控制系统广泛应用于化工、制药、食品加工等多个领域。它通常要求非常精确和稳定的温度控制。在这样的系统中，Z-N法可以有效地减少系统到达设定温度的时间，并最小化超调和振荡。

下面我们将通过一个简单的温度控制案例来说明Z-N