机器学习模型中的数据分布假设：对实际影响的分析，深刻见解

# 1. 数据分布假设的理论基础

在探讨数据分布假设之前，我们必须对数据分布有一个基本的理解。数据分布，简单来说，是数据点在度量空间中的组织方式。它是我们理解数据特性的一个基本工具。无论是在统计学、机器学习还是深度学习领域，数据分布的假设都是构建、评估和选择模型的一个核心部分。

数据分布可以有多种形式，如连续分布或离散分布、均匀分布、正态分布等。这些分布的特点和性质是我们进行假设检验和后续分析的基础。理解并正确应用这些分布假设，对于预测模型的准确性、稳定性和泛化能力至关重要。

在本章中，我们将介绍数据分布的基本概念，探讨其在不同场景下的表现和重要性。我们将从分布的基本定义开始，一步步深入到分布假设的含义和作用，为进一步探讨数据分布假设与机器学习模型的关系奠定理论基础。

# 2. 数据分布假设与机器学习模型的关系

## 2.1 假设检验与模型性能

### 2.1.1 统计假设的含义和作用
在机器学习和统计学中，统计假设是一种关于数据集的主张，它通常包括一个或多个参数的假设。这些假设可以是关于数据分布的形状、均值、方差等属性的。在模型评估和选择过程中，我们通常需要对这些假设进行检验，以确保我们的模型和数据处理方法是合适的。

统计假设检验通常涉及以下几个步骤：
1. 确定原假设（H0）和备择假设（H1）。原假设通常是关于参数的无效应假设，而备择假设则表明效应是存在的。
2. 选择一个检验统计量，例如t统计量、卡方统计量等，这取决于我们对什么进行检验。
3. 根据数据计算检验统计量的值。
4. 根据预设的显著性水平（α），确定临界值或使用p值来决定是否拒绝原假设。

例如，在线性回归模型中，我们可能假设误差项服从正态分布。这个假设可以通过残差分析来检验，我们可以使用正态性检验（如Shapiro-Wilk检验）来确认残差是否符合正态分布。

### 2.1.2 假设检验在模型评估中的应用
在实际应用中，模型评估往往涉及一系列的统计检验，以确保模型的预测能力不仅在训练集上表现良好，而且在未知数据上也能保持稳定的表现。这种检验可以是交叉验证的方法，也可以是模型性能指标（如准确率、召回率、F1分数等）的统计测试。

例如，假设我们使用了一个分类模型，并且希望验证它的预测是否显著优于随机猜测。在这种情况下，我们可以采用McNemar测试来检验两个相关样本（例如，一个模型的预测和随机猜测的结果）之间的差异是否具有统计学意义。

进行假设检验时，我们通常要关注p值。p值是观察到的数据或更极端数据出现的概率，如果这个概率小于显著性水平（通常为0.05），则拒绝原假设。例如，在一个卡方拟合优度检验中，如果p值小于α，我们可以说样本数据与原假设的分布不一致，从而拒绝它。

## 2.2 数据分布的类型及其对模型的影响

### 2.2.1 常见数据分布类型概述
在机器学习中，常见的数据分布类型包括高斯分布（正态分布）、均匀分布、二项分布、泊松分布等。这些分布类型对模型的选择、训练过程和最终性能有着不同的影响。

- 高斯分布（正态分布）：许多自然现象和数据集都趋向于呈现高斯分布。在机器学习中，许多算法默认输入数据遵循高斯分布，例如线性回归、朴素贝叶斯分类器等。
- 均匀分布：数据值均匀分布在某个区间内，其概率密度函数是恒定的。这种分布通常不常见于自然现象，但在某些人工合成数据集或随机过程的建模中可能出现。
- 二项分布：实验只有两种结果（成功或失败），且成功概率为p的独立重复试验的总成功次数的分布。适用于二分类问题，如逻辑回归、朴素贝叶斯分类器等。
- 泊松分布：描述单位时间（或单位面积）内随机事件发生次数的概率分布，适合建模罕见事件的数量，如客流量、呼叫中心的来电量等。

每种分布类型都有其特定的数学性质和适用条件。了解和识别数据的分布类型对于选择合适的机器学习模型至关重要。

### 2.2.2 各类分布对模型选择和训练的影响
数据分布对于选择机器学习模型和调参有着直接的影响。例如：
- 对于高斯分布的数据，线性模型（如线性回归）通常表现良好。而在逻辑回归模型中，数据虽然不一定需要严格服从正态分布，但是残差的分布状况会影响模型预测的准确性。
- 当数据呈现二项分布或二分类问题时，逻辑回归或朴素贝叶斯等分类模型更为合适。
- 对于泊松分布的计数数据，泊松回归或负二项回归可能更适用。

此外，数据分布的特定形状也会影响模型的训练。例如，如果数据存在离群点，可能会导致线性模型等对离群点敏感的模型性能下降。在这种情况下，可能需要考虑鲁棒性更强的模型或先对数据进行变换处理。

## 2.3 理论与实践：分布假设的验证方法

### 2.3.1 分布假设验证的理论基础
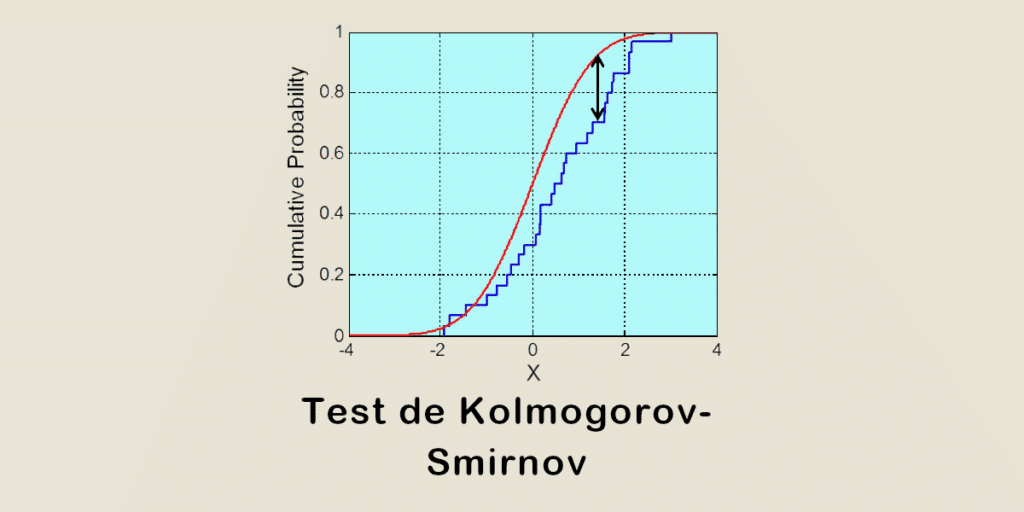
验证数据分布假设的理论基础是统计检验。常用的方法包括Kolmogorov-Smirnov检验、Shapiro-Wilk检验、Anderson-Darling检验等，它们用来检验数据是否服从特定的分布，如正态分布。这些检验通常给出一个统计量和对应的p值，用以判断数据是否与原假设所假设的分布一致。

例如，Shapiro-Wilk检验特别适用于检验样本大小较小的数据集是否服从正态分布。这个检验的统计量是基于数据的顺序统计量来计算的，它对数据分布的尾部更为敏感。

### 2.3.2 实际案例中的验证技术与工具
在实际操作中，我们可以使用各种统计软件或编程语言中的库来执行分布假设检验。例如，使用Python的`scipy`库中的`stats.shapiro`函数可以进行Shapiro-Wilk检验：

import scipy.stats as stats

# 假设data是我们的数据样本
data = [...]  # 用实际数据替换这里的[...]

# Shapiro-Wilk检验
stat, p = stats.shapiro(data)

print('statistic = %.3f, p-value = %.3f' % (stat, p))

如果p值小于我们事先设定的显著性水平（如0.05），则拒绝原假设，表明数据不符合正态分布。此外，还可以使用可视化技术，例如QQ图（Quantile-Quantile Plot），来直观地判断数据的分布情况：

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布数据作为参考线
y = np.random.normal(loc=np.mean(data), scale=np.std(data), size=len(data))
x = np.sort(data)

# 绘制QQ图
plt.scatter(x, y)
plt.title("Q-Q Plot")
plt.xlabel("Theoretical Quantiles")
plt.ylabel("Sample Quantiles")
plt.grid(True)
plt.show()

在QQ图中，如果数据点紧密地遵循参考线，那么数据很可能是正态分布的。如果点显著偏离参考线，则数据不服从正态分布。

通过理论与实践相结合的方式，我们可以确保在机器学习模型中正确地应用和验证数据分布假设，从而优化模型性能和预测准确性。

# 3. 数据分布假设在特定模型中的应用分析

数据分布假设是机器学习中一个关键的概念，它涉及到数据在进行模型训练之前必须满足的一系列统计性质。不同的机器学习模型对数据的分布有不同的假设和要求。本章将深入探讨这些假设在监督学习、无监督学习以及深度学习模型中的具体应用，并分析如何根据数据分布的不同来选择和调整模型。

## 3.1 监督学习模型中的分布假设

在监督学习模型中，理解数据的分布对于模型性能的提升至关重要。这一部分将重点分析两种常见的监督学习模型：线性回归和决策树，以及它们与数据分布假设的关系。

### 3.1.1 线性回归与正态分布假设

线性回归模型是机器学习中最基础且广泛使用的模型之一。该模型假设数据中的特征与目标变量之间存在线性关系，并且在理想状态下，目标变量的误差项（残差）应服从正态分布。这一假设称为线性回归的高斯误差假设。

#### 3.1.1.1 理解正态分布假设

正态分布，亦称高斯分布，是连续概率分布的一种，广泛用于自然科学和社会科学的许多领域。在统计学中，许多统计方法都基于数据遵循正态分布的假设。线性回归模型中，残差的正态分布假设至关重要，因为它影响模型估计的准确性和结果的可靠性。

import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

# 生成一组服从正态分布的数据
data = np.random.normal(loc=0.0, scale=1.0, size=1000)

# 绘制直方图和正态分布曲线
count, bins, ignored = plt.hist(data, 30, density=True)
plt.plot(bins, 1/(0.4 * np.sqrt(2 * np.pi)) * np.exp(- (bins - 0.0)**2 / (2 * 0.4**2)), linewidth=2, color='r')

plt.show()

在上述代码块中，首先利用numpy生成了服从正态分布的数据，并绘制了数据的直方图。然后，使用scipy.stats中的函数绘制了正态分布曲线。通过该代码块，我们可以直观地理解数据分布的形态。

#### 3.1.1.2 正态分布假设的验证

在应用线性回归模型前，应验证残差是否满足正态分布的假设。常用的检验方法包括Q-Q图和Shapiro-Wilk检验等。

from scipy import stats
import matplotlib.pyplot as plt

# 假设这是通过线性回归得到的残差
residuals = ...

# 利用Shapiro-Wilk检验残差的正态性
stat, p_value = stats.shapiro(residuals)

# 输出Shapiro-Wilk检验的结果
print(f"Shapiro-Wilk Test Statistic: {stat:.3f}, p-value: {p_value:.3f}")

在这个代码块中，使用了Scipy库中的Shapiro-Wilk检验来验证残差是否