机器学习特征分布分析：寻找模式与异常，专家级分析工具箱

# 1. 特征分布分析在机器学习中的重要性

在当今数据驱动的世界中，机器学习模型的效能往往取决于数据的质量和特征的代表性。特征分布分析是这一过程中的核心组成部分，它涉及理解数据的分布情况，评估特征的重要性以及确定是否存在异常值或偏差。通过这种分析，我们能够更好地理解数据集的内在结构，为后续的模型训练奠定坚实的基础。

数据分布的洞察力不仅影响着特征工程和模型选择，还直接关系到模型性能的优化。例如，当数据呈现非对称或长尾分布时，常见的机器学习算法可能无法有效地捕捉到数据的真实模式，从而导致预测能力的下降。因此，深入探讨和应用特征分布分析，是推动机器学习领域进步的关键所在。

本章接下来将展开介绍特征分布分析在机器学习中的重要性，包括它是如何帮助我们进行数据预处理、特征选择和异常检测的。我们将探讨分布分析对于模型建立和维护的重要性，以及如何在实际应用中运用这一分析来提高机器学习项目的成功率。

# 2. 理论基础与统计模型

### 2.1 统计学基础回顾

#### 2.1.1 基本统计概念和定义

统计学是机器学习模型构建和评估的基石，它涉及数据的收集、分析、解释、展示和组织。首先，我们要回顾一些基本的统计学概念和定义，这些概念对于理解后续内容至关重要。

- **总体和样本**：在统计学中，总体指的是研究对象的整个集合，而样本是从总体中抽取的一部分个体。通常，我们通过研究样本以推断总体的特征。
- **参数和统计量**：参数是指描述总体特征的数值，例如平均值、标准差等。统计量则是基于样本计算出的，用于估计总体参数的量。
- **离散和连续变量**：离散变量的取值是有限或可数的，如人数；连续变量的取值可以是任意值，如人的身高。

#### 2.1.2 常用的概率分布

概率分布描述了一个随机变量可能出现的取值及其相应的概率。理解常用概率分布对机器学习中特征分布分析极为重要。

- **二项分布**：描述了在固定次数的独立实验中成功次数的概率分布，其参数为实验次数n和每次成功的概率p。
- **正态分布**：是自然界中最常见的连续概率分布之一，其参数为均值μ和标准差σ。
- **泊松分布**：描述在固定时间或空间内发生某事件的次数的概率分布，适用于描述稀有事件。

### 2.2 特征分布分析的理论框架

#### 2.2.1 数据分布的类型

在机器学习中，数据分布可以是单变量的，也可以是多变量的。单变量分布分析通常处理的是单个特征的数据分布情况，而多变量分布分析则关注多个特征之间的联合分布。

- **单变量分布**：通常用于描述一个特征变量的分布情况，如直方图和箱形图。
- **多变量分布**：用于描述两个或两个以上变量的联合分布，涉及的统计方法有协方差矩阵、相关系数等。

#### 2.2.2 分布中心趋势与分散性度量

为了全面理解数据分布，我们必须计算中心趋势和分散性度量。

- **中心趋势度量**：包括均值、中位数和众数。它们描述了数据集的中心位置。
- **分散性度量**：包括方差、标准差和四分位距。它们描述了数据的离散程度或变化范围。

#### 2.2.3 多变量分布分析

多变量分布分析涉及多个特征之间的关系。在机器学习中，这通常用于特征间的相关性分析、多元回归分析等。

- **协方差**：衡量两个特征之间线性关系的统计量。
- **相关系数**：衡量两个特征之间的相关性强度和方向。

### 2.3 分布分析在机器学习中的应用

#### 2.3.1 数据预处理的作用

数据预处理是机器学习中非常关键的步骤，分布分析在这一环节中扮演着重要角色。

- **数据清洗**：通过检查数据的分布情况，可以发现异常值和缺失值。
- **特征缩放**：数据的缩放对于基于距离的算法尤其重要，如K-近邻（KNN）和主成分分析（PCA）。

#### 2.3.2 特征选择与降维

特征选择和降维是提高模型性能的重要手段，它们依赖于特征分布的分析。

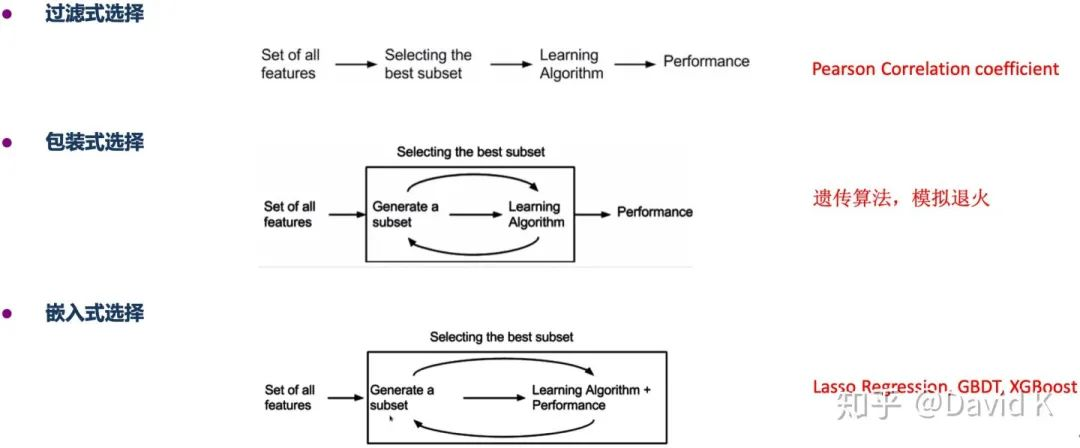
- **特征选择方法**：如信息增益、卡方检验等，它们依赖于特征分布与目标变量的关系。
- **降维技术**：如主成分分析（PCA），它们通过变换将数据映射到低维空间，保持数据分布的重要特征。

#### 2.3.3 异常检测与模式识别

异常检测和模式识别是机器学习中的两个常见应用，特征分布分析在这些应用中同样发挥了巨大的作用。

- **异常检测**：通过统计模型来确定数据点是否为异常值。如使用Z-分数、IQR等方法。
- **模式识别**：利用分布分析来识别数据中的模式，如聚类分析中的K-means算法利用均值将数据点分到多个组。

graph LR
A[数据预处理] --> B[异常值检测]
B --> C[数据清洗]
A --> D[特征缩放]
D --> E[归一化]
E --> F[标准化]

在下一章中，我们将深入探讨如何使用具体的工具和编程语言来实践特征分布的可视化和分析。我们将介绍如何使用Python和R语言来实现各种统计模型，以及一些高级的特征处理技术。

# 3. 实践技巧与工具使用

## 3.1 特征分布的可视化工具

在数据分析和机器学习的实践中，可视化是探索和理解数据特征分布的重要工具。它使得数据科学家能够快速识别数据的模式、趋势和异常值，为后续的数据处理和模型训练提供直观的依据。

### 3.1.1 常用的可视化库和工具

在众多的可视化库中，Python的matplotlib和seaborn是最为常用的库，它们不仅功能强大，而且拥有大量的社区支持和丰富的文档。R语言的ggplot2也是一个强大的可视化工具，它基于“图形语法”理论，可以创建高度定制和美观的图形。此外，还有一些交互式可视化工具，比如Tableau和PowerBI，可以创建动态和可交互的可视化图表，这些工具在业务和报告场景中非常受欢迎。

### 3.1.2 实践中的可视化技巧

在实践中，数据的分布可以通过直方图、箱线图、散点图等直观展示。例如，使用Python的matplotlib库可以这样创建一个数据集的直方图：

import matplotlib.pyplot as plt
import numpy as np

# 创建一个随机正态分布的数据集
data = np.random.normal(0, 1, 1000)

# 创建直方图
plt.hist(data, bins=30, alpha=0.7, color='blue')

# 添加标题和标签
plt.title('Histogram of the dataset')
plt.xlabel('Value')
plt.ylabel('Frequency')

# 显示图形
plt.show()

该代码块展示了如何用Python的matplotlib库生成并展示数据集的直方图。直方图通过将数据值范围分组到连续的区间（或“bins”）中来展示数据的分布情况。

## 3.2 分布分析的编程实践

编程实践是特征分布分析中的核心环节。掌握如何使用编程语言进行分布分析，可以有效地对数据集进行特征提取和预处理。

### 3.2.1 使用Python进行分布分析

Python是目前数据科学领域最受欢迎的编程语言之一。它拥有大量的数据处理和机器学习库。在分布分析中，我们可以使用pandas进行数据操作，使用scipy进行统计计算，使用numpy进行数值计算等。下面是一个使用scipy的统计测试示例：

from scipy import stats
import numpy as np

# 生成两个随机正态分布的数据集
data1 = np.random.normal(0, 1, 1000)
data2 = np.random.normal(0.5, 1, 1000)

# 使用scipy的t-test来检验两个样本的均值是否存在显著差异
t_statistic, p_value = stats.ttest_ind(data1, data2)

print("t-statistic:", t_statistic)
print("p-value:", p_value)

该代码块演示了如何使用scipy中的`stats.ttest_ind`函数来执行两个独立样本t检验，这个统计测试可以用来判断两个数据集的均值是否存在显著差异。

### 3.2.2 使用R语言进行分布分析

R语言在统计分析和学术研究中非常流行。它拥有强大的统计分析和图形功能。例如，下面的R代码展示了如何使用t检验来比较两个样本的均值差异：

# 生成两个随机正态分布的数据集
data1 <- rnorm(1000, mean=0, sd=1)
data2 <- rnorm(1000, mean=0.5, sd=1)

# 使用t检验来检验两个样本的均值是否存在显著差异
t_test_result <- t.test(data1, data2)