揭秘MATLAB带通滤波器：10个实战案例，让你从入门到精通

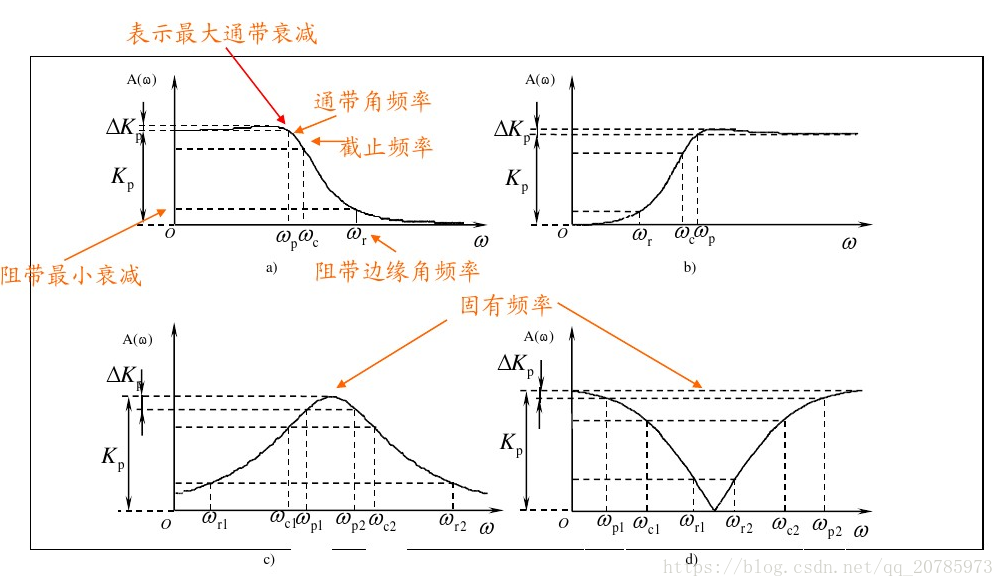
# 1. MATLAB带通滤波器简介

带通滤波器是一种数字滤波器，它允许特定频率范围内的信号通过，同时衰减其他频率范围内的信号。在MATLAB中，可以使用各种函数和工具来设计和实现带通滤波器，这些滤波器在信号处理、图像处理和通信等领域有广泛的应用。

本章将介绍带通滤波器的基本概念、MATLAB中带通滤波器的设计和实现方法，以及一些常见的应用场景。通过对这些内容的理解，读者可以掌握带通滤波器的原理和使用方法，并将其应用于实际问题中。

# 2. 带通滤波器理论基础**

## 2.1 傅里叶变换与频域分析

### 傅里叶变换

傅里叶变换是一种数学变换，它将时域信号（如时间序列）转换为频域信号（如频率谱）。通过傅里叶变换，我们可以分析信号中不同频率成分的分布。

**代码块 1：傅里叶变换**

x = [1, 2, 3, 4, 5];
X = fft(x);
figure;
stem(abs(X));
title('幅度谱');
xlabel('频率');
ylabel('幅度');

**逻辑分析：**

* `fft()` 函数执行傅里叶变换，将时域信号 `x` 转换为频域信号 `X`。
* `abs()` 函数取复数的绝对值，得到幅度谱。
* `stem()` 函数绘制幅度谱，显示信号中不同频率成分的幅度。

### 频域分析

频域分析是通过傅里叶变换将信号转换为频域，并分析其频率成分的分布。频域分析可以帮助我们识别信号中的特征频率、谐波和噪声。

**表格 1：频域分析术语**

| 术语 | 描述 |
|---|---|
| 基频 | 信号中最主要的频率成分 |
| 谐波 | 基频的倍数频率 |
| 带宽 | 信号中包含有用频率的频率范围 |
| 通带 | 信号通过的频率范围 |
| 阻带 | 信号被衰减的频率范围 |

## 2.2 带通滤波器的设计原则

带通滤波器是一种允许特定频率范围（通带）通过，同时衰减其他频率范围（阻带）的滤波器。带通滤波器的设计原则如下：

### 通带选择

通带是带通滤波器允许通过的频率范围。通带的宽度和中心频率由应用要求决定。

### 阻带衰减

阻带是带通滤波器衰减的频率范围。阻带的衰减程度由滤波器的阶数和类型决定。

### 过渡带

过渡带是通带和阻带之间的频率范围，其中滤波器的幅度响应从通带到阻带平滑过渡。过渡带的宽度和陡度由滤波器的设计方法决定。

### 滤波器类型

带通滤波器可以分为两类：

* **有限脉冲响应 (FIR)** 滤波器：具有线性相位响应，但设计复杂度较高。
* **无限脉冲响应 (IIR)** 滤波器：具有更陡峭的截止，但相位响应是非线性的。

# 3. MATLAB带通滤波器设计与实现

### 3.1 FIR滤波器的设计与实现

#### 3.1.1 窗函数法

窗函数法是一种设计FIR带通滤波器的常用方法。它通过在理想带通滤波器的频域响应上加窗，得到实际可实现的滤波器。常用的窗函数有矩形窗、汉明窗、海明窗等。

**代码块 1：矩形窗FIR带通滤波器设计**

% 滤波器参数
Fs = 1000;           % 采样频率
Fpass1 = 100;        % 通带下限频率
Fpass2 = 200;        % 通带上限频率
Apass = 1;           % 通带增益
Astop = 60;          % 阻带衰减

% 设计滤波器
N = 100;             % 滤波器阶数
Wn = [Fpass1 Fpass2] / (Fs/2);  % 归一化截止频率
b = fir1(N, Wn, 'bandpass', [Apass Astop]);

% 绘制频响
freqz(b, 1, 512, Fs);
title('矩形窗FIR带通滤波器频响');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
grid on;

**逻辑分析：**

* `fir1`函数用于设计FIR滤波器。
* `N`参数指定滤波器阶数。
* `Wn`参数指定归一化截止频率。
* `'bandpass'`参数指定带通滤波器类型。
* `[Apass Astop]`参数指定通带增益和阻带衰减。
* `freqz`函数用于绘制滤波器的频响。

#### 3.1.2 最小二乘法

最小二乘法是一种优化方法，可以设计出满足特定频域响应要求的FIR滤波器。它通过最小化频域响应与目标响应之间的均方误差来求解滤波器系数。

**代码块 2：最小二乘法FIR带通滤波器设计**

% 滤波器参数
Fs = 1000;           % 采样频率
Fpass1 = 100;        % 通带下限频率
Fpass2 = 200;        % 通带上限频率
Apass = 1;           % 通带增益
Astop = 60;          % 阻带衰减

% 设计滤波器
N = 100;             % 滤波器阶数
Wn = [Fpass1 Fpass2] / (Fs/2);  % 归一化截止频率
b = firls(N, Wn, [Apass Astop], 'bandpass');

% 绘制频响
freqz(b, 1, 512, Fs);
title('最小二乘法FIR带通滤波器频响');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
grid on;

**逻辑分析：**

* `firls`函数用于设计FIR滤波器。
* `N`参数指定滤波器阶数。
* `Wn`参数指定归一化截止频率。
* `[Apass Astop]`参数指定通带增益和阻带衰减。
* `'bandpass'`参数指定带通滤波器类型。
* `freqz`函数用于绘制滤波器的频响。

### 3.2 IIR滤波器的设计与实现

#### 3.2.1 巴特沃斯滤波器

巴特沃斯滤波器是一种IIR带通滤波器，具有平坦的通带响应和单调下降的阻带响应。它通过求解巴特沃斯多项式来设计。

**代码块 3：巴特沃斯IIR带通滤波器设计**

% 滤波器参数
Fs = 1000;           % 采样频率
Fpass1 = 100;        % 通带下限频率
Fpass2 = 200;        % 通带上限频率
Apass = 1;           % 通带增益
Astop = 60;          % 阻带衰减

% 设计滤波器
N = 5;              % 滤波器阶数
Wn = [Fpass1 Fpass2] / (Fs/2);  % 归一化截止频率
[b, a] = butter(N, Wn, 'bandpass');

% 绘制频响
freqz(b, a, 512, Fs);
title('巴特沃斯IIR带通滤波器频响');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
grid on;

**逻辑分析：**

* `butter`函数用于设计巴特沃斯滤波器。
* `N`参数指定滤波器阶数。
* `Wn`参数指定归一化截止频率。
* `'bandpass'`参数指定带通滤波器类型。
* `freqz`函数用于绘制滤波器的频响。

#### 3.2.2 切比雪夫滤波器

切比雪夫滤波器是一种IIR带通滤波器，具有比巴特沃斯滤波器更陡峭的阻带衰减。它通过求解切比雪夫多项式来设计。

**代码块 4：切比雪夫IIR带通滤波器设计**

% 滤波器参数
Fs = 1000;           % 采样频率
Fpass1 = 100;        % 通带下限频率
Fpass2 = 200;        % 通带上限频率
Apass = 1;           % 通带增益
Astop = 60;          % 阻带衰减

% 设计滤波器
N = 5;              % 滤波器阶数
Wn = [Fpass1 Fpass2] / (Fs/2);  % 归一化截止频率
[b, a] = cheby2(N, 60, Wn, 'bandpass');

% 绘制频响
freqz(b, a, 512, Fs);
title('切比雪夫IIR带通滤波器频响');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');
grid on;

**逻辑分析：**

* `cheby2`函数用于设计切比雪夫滤波器。
* `N`参数指定滤波器阶数。
* `60`参数指定阻带衰减。
* `Wn`参数指定归一化截止频率。
* `'bandpass'`参数指定带通滤波器类型。
* `freqz`函数用于绘制滤波器的频响。

# 4. MATLAB带通滤波器实战案例

### 4.1 语音信号降噪

语音信号降噪是带通滤波器的一个典型应用场景。语音信号通常包含有用的语音信息以及各种噪声，如背景噪声、环境噪声等。带通滤波器可以有效地滤除这些噪声，从而提高语音信号的清晰度和可懂度。

**MATLAB代码：**

% 导入语音信号
[speech, fs] = audioread('speech.wav');

% 设计带通滤波器
Fpass1 = 300;          % 通带下限频率
Fpass2 = 3000;         % 通带上限频率
Apass = 1;              % 通带衰减
Astop = 60;             % 阻带衰减
N = 100;               % 滤波器阶数

Wn = [Fpass1 Fpass2] / (fs/2);  % 归一化截止频率
[b, a] = butter(N, Wn, 'bandpass');  % 设计巴特沃斯带通滤波器

% 滤波语音信号
speech_filtered = filtfilt(b, a, speech);

% 播放滤波后的语音信号
sound(speech_filtered, fs);

**代码逻辑分析：**

1. 导入语音信号并获取采样率。
2. 设计巴特沃斯带通滤波器，指定通带下限频率、通带上限频率、通带衰减、阻带衰减和滤波器阶数。
3. 计算归一化截止频率。
4. 使用 `butter` 函数设计巴特沃斯带通滤波器，并获取滤波器系数 `b` 和 `a`。
5. 使用 `filtfilt` 函数对语音信号进行滤波，得到滤波后的语音信号。
6. 播放滤波后的语音信号。

### 4.2 图像边缘检测

图像边缘检测是计算机视觉中的一项基本任务，它可以提取图像中的边缘信息，从而用于对象识别、图像分割等应用。带通滤波器可以有效地增强图像边缘，从而提高边缘检测的精度。

**MATLAB代码：**

% 导入图像
image = imread('image.jpg');

% 转化为灰度图像
image_gray = rgb2gray(image);

% 设计带通滤波器
Fpass1 = 0.1;          % 通带下限频率
Fpass2 = 0.5;          % 通带上限频率
Apass = 1;              % 通带衰减
Astop = 60;             % 阻带衰减
N = 100;               % 滤波器阶数

Wn = [Fpass1 Fpass2];  % 归一化截止频率
[b, a] = butter(N, Wn, 'bandpass');  % 设计巴特沃斯带通滤波器

% 滤波图像
image_filtered = imfilter(image_gray, b, a);

% 显示滤波后的图像
figure;
imshow(image_filtered);

**代码逻辑分析：**

1. 导入图像并转换为灰度图像。
2. 设计巴特沃斯带通滤波器，指定通带下限频率、通带上限频率、通带衰减、阻带衰减和滤波器阶数。
3. 计算归一化截止频率。
4. 使用 `butter` 函数设计巴特沃斯带通滤波器，并获取滤波器系数 `b` 和 `a`。
5. 使用 `imfilter` 函数对图像进行滤波，得到滤波后的图像。
6. 显示滤波后的图像。

### 4.3 生物医学信号处理

带通滤波器在生物医学信号处理中也发挥着重要作用。例如，在心电图（ECG）信号处理中，带通滤波器可以滤除ECG信号中的噪声和干扰，从而提取有用的心电特征。

**MATLAB代码：**

% 导入ECG信号
ecg = load('ecg.mat');

% 设计带通滤波器
Fpass1 = 0.5;          % 通带下限频率
Fpass2 = 150;         % 通带上限频率
Apass = 1;              % 通带衰减
Astop = 60;             % 阻带衰减
N = 100;               % 滤波器阶数

Wn = [Fpass1 Fpass2] / (ecg.fs/2);  % 归一化截止频率
[b, a] = butter(N, Wn, 'bandpass');  % 设计巴特沃斯带通滤波器

% 滤波ECG信号
ecg_filtered = filtfilt(b, a, ecg.val);

% 绘制滤波后的ECG信号
figure;
plot(ecg.time, ecg_filtered);
xlabel('Time (s)');
ylabel('Amplitude (mV)');
title('Filtered ECG Signal');

**代码逻辑分析：**

1. 导入ECG信号。
2. 设计巴特沃斯带通滤波器，指定通带下限频率、通带上限频率、通带衰减、阻带衰减和滤波器阶数。
3. 计算归一化截止频率。
4. 使用 `butter` 函数设计巴特沃斯带通滤波器，并获取滤波器系数 `b` 和 `a`。
5. 使用 `filtfilt` 函数对ECG信号进行滤波，得到滤波后的ECG信号。
6. 绘制滤波后的ECG信号。

# 5.1 多级带通滤波器的设计

在某些应用中，单级带通滤波器可能无法满足要求，需要设计多级带通滤波器来进一步提高滤波性能。多级带通滤波器可以级联多个单级带通滤波器，从而实现更窄的通带、更陡峭的截止频率和更高的抑制带衰减。

### 级联滤波器设计

级联滤波器设计是将多个单级滤波器串联连接，每个滤波器具有不同的截止频率和通带宽度。通过级联滤波器，可以实现更复杂的滤波特性，例如：

- **窄带带通滤波器：**级联多个窄带带通滤波器，可以实现更窄的通带，提高频率选择性。
- **多通带带通滤波器：**级联多个不同中心频率的带通滤波器，可以实现多个通带，同时滤除其他频率成分。
- **带阻滤波器：**级联一个带通滤波器和一个低通滤波器或高通滤波器，可以实现带阻滤波特性，滤除特定的频率范围。

### 级联滤波器设计步骤

级联滤波器设计步骤如下：

1. **确定滤波器规格：**确定所需的多级带通滤波器的通带、截止频率、通带增益和抑制带衰减。
2. **设计单级滤波器：**根据滤波器规格，设计每个单级带通滤波器。可以使用MATLAB中的`fir1`或`butter`等函数来设计滤波器。
3. **级联滤波器：**将设计的单级滤波器级联连接，形成多级带通滤波器。可以使用MATLAB中的`cascade`函数来级联滤波器。
4. **验证滤波器性能：**使用MATLAB中的`freqz`函数来验证滤波器的频率响应，确保其满足滤波器规格。

### 代码示例

以下代码示例演示如何设计一个三级窄带带通滤波器：

% 滤波器规格
Fs = 1000;          % 采样频率
Fpass1 = 100;        % 通带下限频率
Fpass2 = 200;        % 通带上限频率
Apass = 1;           % 通带增益
Astop = 60;          % 抑制带衰减

% 设计单级滤波器
N = 100;             % 滤波器阶数
Wn = [Fpass1 Fpass2] / (Fs/2);  % 归一化截止频率
b1 = fir1(N, Wn, 'bandpass');

% 级联滤波器
H = cascade(b1, b1, b1);

% 验证滤波器性能
[H, f] = freqz(H, 1, Fs);
figure;
plot(f, 20*log10(abs(H)));
title('三级窄带带通滤波器频率响应');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');