MATLAB带通滤波器与傅里叶变换：频率域滤波揭秘，提升图像处理效果

# 1. MATLAB数字信号处理概述

MATLAB是一种广泛用于数字信号处理(DSP)的编程语言和交互式环境。它提供了丰富的工具和函数，使工程师和研究人员能够轻松高效地处理、分析和可视化信号数据。

MATLAB的DSP功能包括：

- 信号生成和操作
- 傅里叶变换和频域分析
- 滤波器设计和实现
- 图像处理和计算机视觉
- 统计信号处理

# 2. 傅里叶变换与频率域分析

### 2.1 傅里叶变换的理论基础

#### 2.1.1 时域和频域概念

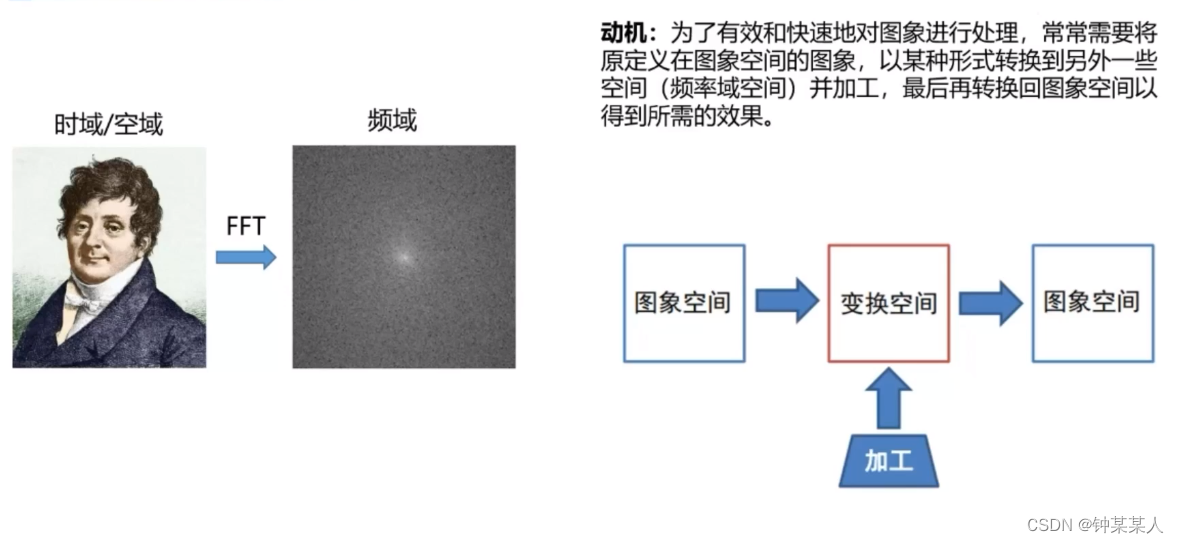
时域是指信号随时间的变化，而频域是指信号中不同频率分量的分布。傅里叶变换将时域信号分解为一系列正弦波，每个正弦波对应一个特定的频率。

#### 2.1.2 傅里叶变换的定义和性质

傅里叶变换将一个时域信号 `x(t)` 转换为一个频域信号 `X(f)`，其定义如下：

X(f) = ∫_{-\infty}^{\infty} x(t) e^(-j2πft) dt

其中，`f` 为频率。

傅里叶变换具有以下性质：

* **线性：**傅里叶变换是线性的，即 `F(aX(t) + bY(t)) = aF(X(t)) + bF(Y(t))`。
* **时移：**时域信号的时移对应频域信号的相移。
* **频移：**频域信号的频移对应时域信号的调制。
* **卷积：**时域信号的卷积对应频域信号的乘积。

### 2.2 傅里叶变换在MATLAB中的实现

#### 2.2.1 fft和ifft函数的使用

MATLAB中提供了 `fft` 和 `ifft` 函数来计算傅里叶变换和逆傅里叶变换。`fft` 函数将时域信号转换为频域信号，而 `ifft` 函数将频域信号转换为时域信号。

% 时域信号
x = [1, 2, 3, 4, 5];

% 计算傅里叶变换
X = fft(x);

% 计算逆傅里叶变换
x_reconstructed = ifft(X);

#### 2.2.2 频率域图表的绘制

要绘制频率域图表，可以使用 MATLAB 的 `stem` 函数。

% 绘制频率域图表
stem(abs(X));
xlabel('频率');
ylabel('幅度');

此代码将绘制频域信号的幅度谱。

# 3. MATLAB带通滤波器设计

### 3.1 带通滤波器的原理和应用

#### 3.1.1 带通滤波器的特性

带通滤波器是一种线性滤波器，它允许特定频率范围内的信号通过，而衰减其他频率范围的信号。带通滤波器的频率响应曲线呈带状，在通带内具有较高的增益，而在阻带内具有较低的增益。

带通滤波器的特性由其通带频率、阻带频率和通带增益决定。通带频率是指信号通过时增益保持在较高水平的频率范围，阻带频率是指信号通过时增益衰减到较低水平的频率范围，通带增益是指通带内信号的增益。

#### 3.1.2 带通滤波器的应用场景

带通滤波器在信号处理和图像处理等领域有着广泛的应用。在信号处理中，带通滤波器可用于提取特定频率范围的信号，例如在语音信号处理中提取语音信号的基频。在图像处理中，带通滤波器可用于图像去噪、边缘检测和纹理分析。

### 3.2 带通滤波器的MATLAB实现

#### 3.2.1 fir1函数的