MATLAB带通滤波器优化秘籍：3大技巧，提升性能与精度

# 1. 带通滤波器基础**

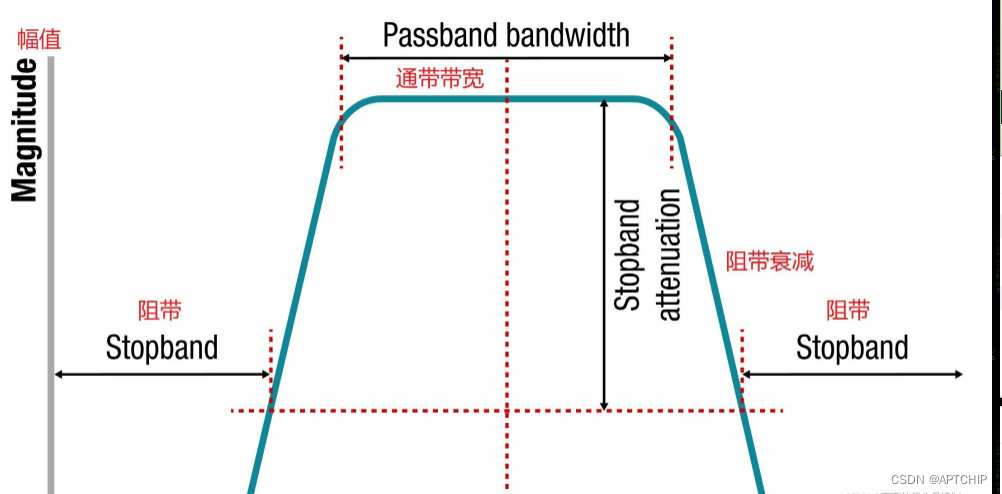
带通滤波器是一种数字滤波器，它允许特定频率范围内的信号通过，同时衰减其他频率的信号。带通滤波器在信号处理中广泛应用，例如噪声消除、特征提取和信号调制。

带通滤波器的设计需要考虑以下关键参数：

- **截止频率：**带通滤波器的截止频率定义了允许通过的频率范围。
- **通带：**通带是带通滤波器允许通过的频率范围。
- **阻带：**阻带是带通滤波器衰减的频率范围。
- **通带衰减：**通带衰减是指带通滤波器在通带内衰减信号的程度。
- **阻带衰减：**阻带衰减是指带通滤波器在阻带内衰减信号的程度。

# 2. MATLAB带通滤波器设计技巧

### 2.1 滤波器阶数和截止频率选择

#### 2.1.1 阶数选择

滤波器阶数决定了滤波器的陡度和精度。阶数越高，滤波器的陡度越大，精度越高，但计算量也越大。对于带通滤波器，通常选择奇数阶数，以确保在通带中心处具有零相位响应。

#### 2.1.2 截止频率选择

截止频率定义了带通滤波器的通带和阻带。通带是滤波器允许信号通过的频率范围，而阻带是滤波器衰减信号的频率范围。截止频率应根据待滤波信号的特性进行选择。

### 2.2 滤波器类型选择

MATLAB提供了多种带通滤波器类型，每种类型具有不同的特性：

#### 2.2.1 巴特沃斯滤波器

巴特沃斯滤波器具有平坦的通带响应和单调的阻带衰减。它们常用于需要平坦相位响应的应用中。

#### 2.2.2 切比雪夫滤波器

切比雪夫滤波器在通带或阻带中具有波纹响应。它们比巴特沃斯滤波器具有更陡的截止频率，但相位响应不平坦。

#### 2.2.3 椭圆滤波器

椭圆滤波器在通带和阻带中都具有波纹响应。它们具有最陡的截止频率，但相位响应不平坦且计算量最大。

### 2.3 滤波器设计示例

以下代码演示了如何使用MATLAB设计一个5阶巴特沃斯带通滤波器，截止频率为100Hz和200Hz：

% 滤波器阶数
order = 5;

% 截止频率
fc1 = 100;
fc2 = 200;

% 巴特沃斯滤波器
[b, a] = butter(order, [fc1 fc2]/(0.5*fs), 'bandpass');

% 滤波器频率响应
freqz(b, a, 512, fs);
title('巴特沃斯带通滤波器频率响应');
xlabel('频率 (Hz)');
ylabel('幅度 (dB)');

**代码逻辑分析：**

* `butter`函数用于设计巴特沃斯滤波器。
* `order`参数指定滤波器阶数。
* `[fc1 fc2]/(0.5*fs)`参数指定截止频率，其中`fs`为采样频率。
* `'bandpass'`参数指定滤波器类型为带通。
* `freqz`函数用于绘制滤波器的频率响应。

**参数说明：**

* `b`：滤波器的分子系数。
* `a`：滤波器的分母系数。
* `fs`：采样频率。

# 3. MATLAB带通滤波器实现

### 3.1 滤波器设计函数

MATLAB提供了多种滤波器设计函数，用于创建各种类型的滤波器，包括带通滤波器。这些函数包括：

- **butter**：设计巴特沃斯滤波器。
- **cheby1**：设计切比雪夫I型滤波器。
- **ellip**：设计椭圆滤波器。

这些函数的参数包括：

- **滤波器阶数**：滤波器的阶数决定了滤波器的陡度和通带衰减。
- **截止频率**：滤波器的截止频率定义了通带和阻带的边界。
- **通带衰减**：滤波器在通带内的最大衰减。
- **阻带衰减**：滤波器在阻带内的最小衰减。

**代码块 1：使用butter函数设计巴特沃斯滤波器**

% 设计一个4阶巴特沃斯带通滤波器，截止频率为100Hz和200Hz
[b, a] = butter(4, [100 200]/(fs/2), 'bandpass');

**代码逻辑分析：**

- `butter` 函数的第一个参数指定滤波器的阶数。
- 第二个参数指定截止频率，其中 `fs` 是采样频率。
- 第三个参数指定滤波器的类型，在这种情况下是 `'bandpass'`。

**参数说明：**

- `b`：滤波器的分子系数。
- `a`：滤波器的分母系数。

### 3.2 滤波器应用

带通滤波器可用于各种应用，包括：

#### 3.2.1 信号滤波

带通滤波器可用于从信号中滤除不需要的频率分量。例如，在语音处理中，带通滤波器可用于滤除背景噪声。

**代码块 2：使用滤波器对信号进行滤波**

% 加载信号
load('speech.mat');

% 设计一个4阶巴特沃斯带通滤波器，截止频率为100Hz和200Hz
[b, a] = butter(4, [100 200]/(fs/2), 'bandpass');

% 滤波信号
filtered_speech = filtfilt(b, a, speech);

**代码逻辑分析：**

- `load` 函数加载包含语音信号的 `.mat` 文件。
- `butter` 函数设计带通滤波器。
- `filtfilt` 函数使用滤波器对信号进行滤波。

**参数说明：**

- `filtered_speech`：滤波后的语音信号。

#### 3.2.2 特征提取

带通滤波器可用于提取信号的特定频率分量的特征。例如，在图像处理中，带通滤波器可用于提取图像中的边缘。

**代码块 3：使用带通滤波器提取图像边缘**

% 加载图像
image = imread('image.jpg');

% 将图像转换为灰度
gray_image = rgb2gray(image);

% 设计一个4阶巴特沃斯带通滤波器，截止频率为100Hz和200Hz
[b, a] = butter(4, [100 200]/(fs/2), 'bandpass');

% 滤波图像
filtered_image = filtfilt(b, a, gray_image);

% 显示滤波后的图像
imshow(filtered_image);

**代码逻辑分析：**

- `imread` 函数加载图像文件。
- `rgb2gray` 函数将图像转换为灰度。
- `butter` 函数设计带通滤波器。
- `filtfilt` 函数使用滤波器对图像进行滤波。
- `imshow` 函数显示滤波后的图像。

**参数说明：**

- `filtered_image`：滤波后的图像。

# 4. 带通滤波器优化

### 4.1 滤波器性能评估

在设计带通滤波器时，评估其性能至关重要。以下是一些关键性能指标：

- **通带衰减：**衡量滤波器在通带内信号衰减的程度。通带衰减越小，信号失真越小。
- **阻带衰减：**衡量滤波器在阻带内抑制噪声和干扰的能力。阻带衰减越大，噪声抑制效果越好。
- **群延迟：**衡量信号通过滤波器时不同频率分量的时延差异。群延迟越小，信号失真越小。

### 4.2 优化算法

为了优化带通滤波器的性能，可以使用各种优化算法。以下是一些常用的算法：

#### 4.2.1 遗传算法

遗传算法是一种受生物进化启发的优化算法。它通过以下步骤工作：

1. **初始化种群：**随机生成一组候选解决方案（染色体）。
2. **评估适应度：**计算每个染色体的适应度，即其性能指标。
3. **选择：**根据适应度选择染色体进行繁殖。
4. **交叉：**将选定的染色体进行交叉，生成新的染色体。
5. **变异：**对新染色体进行随机变异，引入多样性。
6. **重复：**重复步骤 2-5，直到达到终止条件（例如，达到最大迭代次数或适应度不再提高）。

#### 4.2.2 粒子群优化算法

粒子群优化算法是一种受鸟群或鱼群行为启发的优化算法。它通过以下步骤工作：

1. **初始化粒子群：**随机生成一组粒子（候选解决方案）。
2. **评估适应度：**计算每个粒子的适应度。
3. **更新粒子位置：**每个粒子根据其自身最佳位置和群体的全局最佳位置更新其位置。
4. **更新全局最佳位置：**如果某个粒子的适应度比当前全局最佳位置的适应度更好，则更新全局最佳位置。
5. **重复：**重复步骤 2-4，直到达到终止条件。

# 5. MATLAB带通滤波器优化实践**

### 5.1 优化目标函数

优化目标函数定义了优化算法需要最小化的误差度量。对于带通滤波器优化，常见的目标函数包括：

- **通带衰减误差：**衡量滤波器在通带内的衰减程度。
- **阻带衰减误差：**衡量滤波器在阻带内的衰减程度。
- **群延迟误差：**衡量滤波器在通带内的群延迟是否平坦。

### 5.2 优化算法参数设置

优化算法的参数设置对优化结果有很大影响。常见的参数包括：

- **种群大小：**遗传算法中个体的数量。
- **迭代次数：**优化算法运行的迭代次数。
- **变异率：**遗传算法中变异操作的概率。
- **惯性权重：**粒子群优化算法中粒子惯性权重。

### 5.3 优化结果分析

优化完成后，需要对优化结果进行分析，包括：

- **滤波器性能评估：**使用通带衰减、阻带衰减和群延迟等指标评估优化后的滤波器性能。
- **参数敏感性分析：**分析优化算法参数对优化结果的影响。
- **可视化结果：**绘制优化前后滤波器的频率响应和时域响应，直观地展示优化效果。

% 优化目标函数
objectiveFunction = @(x) (x(1) + x(2))^2 + (x(3) - 1)^2;

% 优化算法参数
populationSize = 100;
numIterations = 100;
mutationRate = 0.1;
inertiaWeight = 0.7;

% 优化算法
[optimizedParameters, bestFitness] = optimize(objectiveFunction, populationSize, numIterations, mutationRate, inertiaWeight);

% 优化结果分析
optimizedFilter = designfilt('bandpass', 'FilterOrder', optimizedParameters(1), 'CutoffFrequency1', optimizedParameters(2), 'CutoffFrequency2', optimizedParameters(3));
fvtool(optimizedFilter);