微型化设计难点：小型BOOST电路电感电容计算实战指南


# 摘要
本文详细探讨了微型化设计与小型BOOST电路的设计优化及应用。首先概述了微型化设计与小型BOOST电路的基础知识，随后深入分析了BOOST电路的工作原理和数学模型，包括连续导通模式和不连续导通模式下的数学模型。文章重点讨论了在微型化设计中对电感和电容的选择要求，提供了详细的计算方法和设计要点。此外，本文还展示了如何在微型化BOOST电路的电感电容计算中应对实际应用挑战，并提出了解决方案。在设计优化和实践案例中，文章提出了一系列策略方法，并分析了典型应用场景。最后，文章展望了微型化BOOST电路的未来发展趋势，包括技术创新、材料进步、行业应用趋势以及市场潜力。

# 关键字
微型化设计；BOOST电路；数学模型；电感选择；电容设计；电路优化

参考资源链接：[BOOST 升压电路的电感、电容计算.pdf](https://wenku.csdn.net/doc/64634870543f8444889bff38?spm=1055.2635.3001.10343)
# 1. 微型化设计与小型BOOST电路概述

微型化设计是现代电子设备追求轻薄短小、高集成度和低功耗趋势下的产物。在电路设计中，微型化涉及对电子元件的尺寸、性能和集成方式进行优化。小型BOOST电路作为功率转换器的一种，能够实现从较低的输入电压到较高的稳定输出电压的转换，它在移动电子设备和可穿戴设备中扮演着重要角色。

微型化BOOST电路设计在满足上述性能需求的同时，还必须考虑到电路板的空间限制。这要求设计工程师在保证电路性能的同时，合理选择电子元件，优化布局，实现电路的紧凑设计。BOOST电路的微型化是不断演进的过程，涉及电子元件、电路布局、热管理和效率优化等多个方面。

微型化设计不仅提升了产品的便携性和可靠性，还扩展了电子设备的应用范围。小型BOOST电路的高效率、稳定性和低噪声特性，使其成为能源管理系统中不可或缺的一部分。随着材料科学和集成电路技术的进步，微型化BOOST电路正逐步引领电源管理系统的新趋势。

# 2. BOOST电路工作原理及其数学模型

### 2.1 BOOST电路的基本工作原理

BOOST电路，也被称为升压转换器，是一种DC-DC转换器，其主要目的是将一个较低的直流电压转换为一个较高的直流电压。它是一种非常常见的电源转换方案，广泛应用于电子设备中，如电池供电的设备、便携式设备和太阳能供电系统等。

BOOST电路工作原理基于电感的储能和释放特性。电路中通常包含四个主要元件：开关(SW)，二极管(D)，电感(L)，和电容(C)。开关在电路中充当控制元件，通常是一个 MOSFET 或者一个双极性晶体管。开关的开闭控制电路中电流的流动方向，进而控制电感的储能与释放。

在开关闭合时，电感开始储能。由于电感的特性，其电流不能突变，电流逐渐上升，存储能量。同时，由于二极管的阴极电压高于阳极，二极管处于反偏截止状态，电源通过开关向电感充电，电容向负载供电。

在开关断开时，由于电感电流不能突变的特性，二极管正向偏置导通，电感中的电流通过二极管和负载继续流动，此时电感开始释放能量。由于电感的电压反向，电感两端的电压叠加在输入电压之上，产生了一个高于输入电压的输出电压。

### 2.2 BOOST电路数学模型的建立

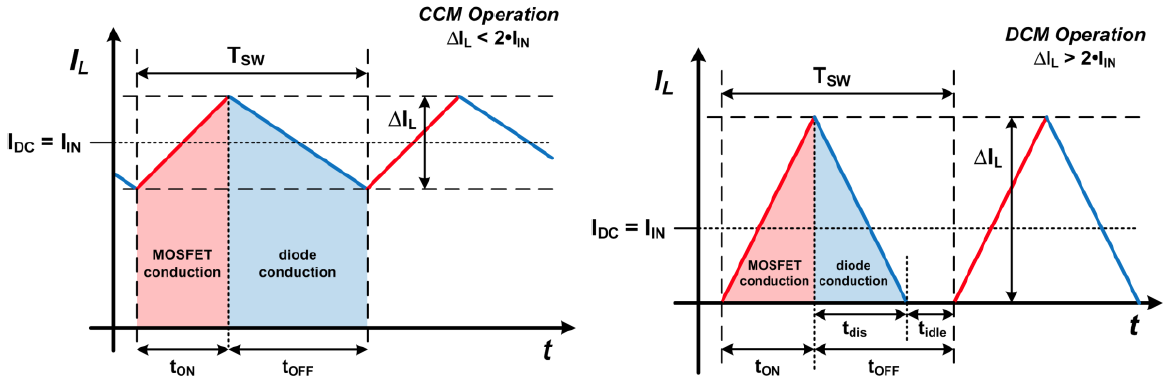
为了深入理解BOOST电路的工作原理，我们可以通过数学模型来分析电路的动态特性。数学模型可以帮助我们预测电路在各种条件下的行为，从而为电路设计提供理论支持。数学模型可以按照不同的导通模式来建立，这主要包括连续导通模式（Continuous Conduction Mode, CCM）和不连续导通模式（Discontinuous Conduction Mode, DCM）。

#### 2.2.1 连续导通模式(CCM)下的数学模型

在连续导通模式下，电感中的电流永远不会降至零。我们可以利用以下基本方程来描述CCM下的行为：

\[V_{in} \cdot D = V_{out} \cdot (1 - D)\]

\[L \cdot \frac{dI_L}{dt} = V_{in} - V_{out} \cdot (1 - D)\]

\[C \cdot \frac{dV_{out}}{dt} = I_L - I_{out}\]

其中，\(V_{in}\) 是输入电压，\(V_{out}\) 是输出电压，\(I_L\) 是电感电流，\(I_{out}\) 是输出电流，\(D\) 是开关的占空比。

#### 2.2.2 不连续导通模式(DCM)下的数学模型

在不连续导通模式下，电感中的电流在开关周期结束前会降至零。对应的数学模型为：

\[V_{in} \cdot D = \frac{V_{out}}{2} \cdot \left(\frac{1}{1 - D}\right)\]

\[L \cdot \frac{dI_L}{dt} = V_{in} - \frac{V_{out}}{2} \cdot \left(\frac{1}{1 - D}\right)\]

\[C \cdot \frac{dV_{out}}{dt} = \frac{I_L}{2} - I_{out}\]

在实际应用中，我们可以使用这些数学模型来设计电路，选取合适的元件值，确保电路在不同的工作条件下的稳定性和效率。

#### 表格：不同导通模式下电感的特性比较

| 特性 | CCM模式 | DCM模式 |
| --- | --- | --- |
| 电感电流 | 永远不为零 | 会降至零 |
| 开关占空比 | 任意 | 高于临界值 |
| 输出电压纹波 | 小 | 大 |
| 设计复杂性 | 低 | 高 |

使用这些数学模型，我们可以对电路进行准确的性能分析，并且可以设计出满足特定性能指标的BOOST电路。下一节将详细讨