MATLAB时域分析：多变量控制系统，挑战与对策的权威指南

# 1. 多变量控制系统简介

在自动化和控制系统领域，多变量控制系统是核心组成部分之一，它涵盖了多个输入和多个输出的复杂交互过程。随着现代技术的发展，这类系统在航空、汽车、电力和机器人技术等领域中扮演着越来越重要的角色。本章将首先介绍多变量控制系统的定义、特点以及它在实际应用中的重要性，为读者提供一个系统的概览。

## 1.1 多变量控制系统的定义

多变量控制系统（Multivariable Control Systems, MCS）是一种控制方法，它涉及多个控制输入变量和多个受控输出变量。与单一输入单一输出（SISO）系统相比，多变量控制系统的每个控制决策都会影响多个输出变量，这就增加了控制策略的设计复杂性。

## 1.2 多变量控制系统的应用领域

多变量控制系统广泛应用于各种工业和科研领域，例如：

- **航空器控制**：飞机在飞行过程中需要同时控制速度、高度、方向等多个变量。
- **汽车电子稳定程序（ESP）**：ESP系统需要协调多个传感器的数据，控制车辆的多个运动参数。
- **电力系统**：发电、输电和配电过程中需要精确控制电压、电流和频率等多个参数。
- **机器人技术**：在机器人控制中，多个电机需要协调工作以实现精确的位置、速度控制。

## 1.3 多变量控制系统的重要性

多变量控制系统之所以重要，是因为它能够处理和优化多个控制目标，提高系统的整体性能和效率。例如，在多目标优化问题中，多变量控制可以同时考虑到多个性能指标，从而达到更为理想的控制效果。此外，多变量控制系统的引入可以提高系统对干扰的抵抗力，增强系统的鲁棒性，这对于确保生产安全和提高产品质量至关重要。

在接下来的章节中，我们将探讨MATLAB这一强大的工具在多变量控制系统中的应用，并深入了解如何通过MATLAB进行系统分析、设计与优化。

# 2. MATLAB在多变量控制系统中的基础应用

## 2.1 MATLAB的控制系统工具箱

### 2.1.1 工具箱中关键函数的使用方法

MATLAB的控制系统工具箱是一套为控制系统设计、分析和仿真提供强大支持的函数集合。它包括了从系统表示、模型转换、稳定性分析到控制器设计等众多功能，是研究和开发控制系统不可或缺的工具。

一个关键的函数是`tf`，它用于创建传递函数模型。传递函数是描述线性时不变系统动态特性的一种数学模型。传递函数模型可以用于系统分析和控制器设计中。

num = [2 5]; % 分子多项式系数
den = [1 2 1]; % 分母多项式系数
sys_tf = tf(num, den); % 创建传递函数模型

在上述代码中，`num`和`den`分别表示传递函数的分子和分母系数，`tf`函数将这些系数组合成一个传递函数对象`sys_tf`。

`step`函数用于计算并绘制系统的阶跃响应。阶跃响应是评估控制系统性能的一个重要指标，它显示了系统对于阶跃输入信号的反应。

step(sys_tf); % 绘制阶跃响应

此外，`bode`函数用于绘制系统的频率响应，包括幅频特性和相频特性，是分析系统频率特性的重要工具。

bode(sys_tf); % 绘制频率响应

这些函数的使用不仅有助于理解系统模型的特性，而且为后续的系统分析和控制器设计提供了基础。

### 2.1.2 系统模型的建立和仿真

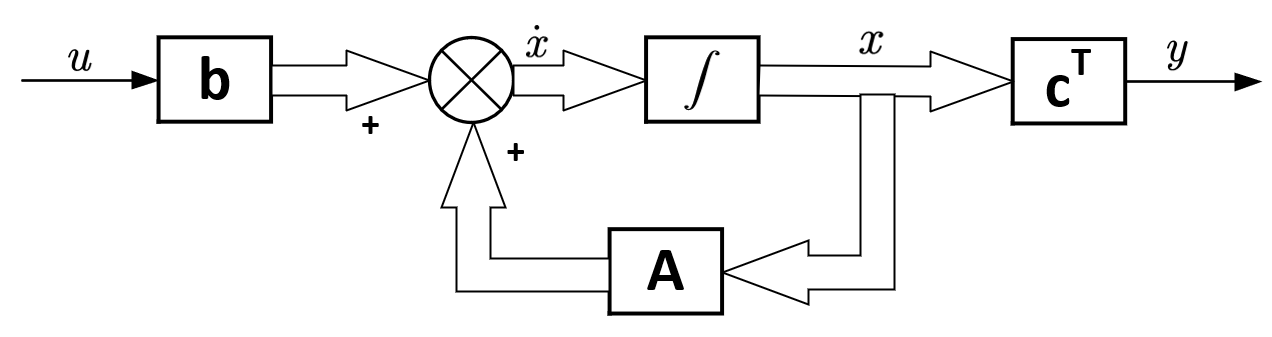
在MATLAB中建立系统模型是进行控制分析的前提。对于多变量控制系统，由于存在多个输入和多个输出，因此需要使用多输入多输出（MIMO）的建模方法。

一个典型的多变量系统可以用状态空间模型来表示，状态空间模型包含系统矩阵A、输入矩阵B、输出矩阵C和直接传输矩阵D。

A = [-1, 2; 3, -4];
B = [1, 0; 0, 1];
C = [0, 1; 1, 0];
D = [0, 0; 0, 0];
sys_ss = ss(A, B, C, D); % 创建状态空间模型

在上述代码中，`A`, `B`, `C`, `D`分别定义了系统的四个矩阵，`ss`函数用于创建状态空间模型`sys_ss`。

仿真多变量系统模型可以使用`lsim`函数，它提供了线性系统对任意输入信号的仿真功能。

u = [sin(0.5*t); cos(t)]; % 定义输入信号
t = 0:0.01:10; % 定义时间向量
lsim(sys_ss, u, t); % 线性系统仿真

通过这样的仿真，我们可以观察到在特定输入作用下系统输出的变化，从而了解系统对输入信号的响应性能。

## 2.2 系统分析的基本理论

### 2.2.1 多变量系统的稳定性分析

稳定性分析是控制理论中的核心问题，对于多变量系统而言，其稳定性分析要复杂得多。对于MIMO系统，稳定性不仅与系统的极点有关，还受到系统矩阵结构和耦合关系的影响。

在MATLAB中，可以通过函数`eig`来计算系统矩阵的特征值，这是判断线性时不变系统稳定性的常用方法。如果所有特征值的实部均为负，则系统是稳定的。

eigenvalues = eig(A); % 计算特征值

判断多变量系统稳定性时，还需要考虑系统的内部动态耦合关系。这种耦合关系可以通过系统的传递函数矩阵或状态空间模型的传递矩阵来分析。

### 2.2.2 系统性能指标的定义和计算

系统性能指标是指衡量系统性能的标准，包括稳态误差、上升时间、峰值时间和稳态值等。在MATLAB中，这些指标可以通过一系列函数来计算。

稳态误差可以通过计算系统传递函数在s=0时的值来确定，这称为静态增益。上升时间和峰值时间等动态特性指标可以通过系统对阶跃输入的响应来获得。

steady_state_error = 1 - dcgain(sys_tf); % 计算稳态误差

在这里，`dcgain`函数计算了传递函数在s=0时的静态增益，从而能够估算出稳态误差。

通过系统性能指标的计算，我们不仅可以评估一个设计好的系统是否满足设计要求，还可以作为优化系统设计的依据。

## 2.3 MATLAB中的控制系统设计

### 2.3.1 反馈控制器设计

反馈控制器设计是控制工程中的一个经典问题。对于多变量系统，设计一个有效的反馈控制器尤为关键，因为这样的系统中各变量之间存在相互影响。

PID控制器是最常见的反馈控制器类型，它通过比例（P）、积分（I）和微分（D）三种控制方式的组合来实现对系统的有效控制。

Kp = 1; Ki = 0.1; Kd = 0.05;
controller_pid = pid(Kp, Ki, Kd); % 创建PID控制器

设计好控制器之后，可以使用`feedback`函数来计算系统的闭环传递函数。

sys_cl = feedback(sys_tf*controller_pid, 1); % 计算闭环传递函数

在这里，`feedback`函数将开环传递函数（控制器和原系统串联）和反馈增益（此处为1，表示单位负反馈）结合起来，得到闭环传递函数`sys_cl`。

### 2.3.2 预测控制器设计

预测控制是一种先进的控制策略，它能够处理复杂的多变量控制系统，并考虑到未来行为的预测。

在MATLAB中，可以使用`mpc`函数来创建和设计模型预测控制器。这种控制器会预测系统在未来一定时间范围内的行为，并优化控制输入以达到期望的输出。

% 设定预测控制器参数
mpc_controller = mpc(sys_ss, Ts, PredictionHorizon, ControlHorizon);

在上述代码中，`sys_ss`是状态空间模型，`Ts`是控制周期，`PredictionHorizon`和`ControlHorizon`分别是预测范围和控制范围。

通过调整预测控制器的参数和约束条件，可以对多变量系统进行有效控制，并实现复杂的控制目标。

# 3. 多变量控制系统在MATLAB中的高级分析

在当今复杂的控制工程领域，对多变量控制系统进行深入分析是至关重要的。第三章将带你进入MATLAB环境下多变量控制系统高级分析的世界，包括鲁棒性分析、多变量系统优化技术和系统仿真的深入探讨。

## 3.1 鲁棒性分析

### 3.1.1 鲁棒性分析的基本概念

鲁棒性（Robustness）是控制系统设计中的一个核心概念，指的是系统在各种不确定性和外部扰动下保持性能稳定的能力。一个鲁棒的控制系统能够经受住模型参数变化、外部噪声干扰以及设备老化等影响而不失其性能。

### 3.1.2 MATLAB中的鲁棒性分析工具

在MATLAB中，我们可以通过一系列工具和函数来进行鲁棒性分析。例如，`robuststab`和`robustmargin`函数可以帮助我们评估系统稳定裕度和鲁棒性边界。此外，`mu工具箱`提供了计算系统多变量鲁棒稳定