【算法选型】PID与其他巡线算法对决：优劣势大揭秘


# 摘要
巡线算法是智能系统导航和路径规划的核心技术，本文全面探讨了巡线算法的基础知识、理论与实践应用，尤其关注了PID算法及其性能优化。通过分析PID算法的基本原理、编程实现以及与其他巡线算法的对比，本文深入讨论了不同算法在静态和动态环境下的应用选择及综合应用策略。同时，本文对巡线算法的未来发展趋势进行了展望，重点强调了人工智能技术、新兴传感器技术与跨学科合作在推动巡线算法创新方面的重要性。本文的研究为相关领域的研究者和工程技术人员提供了理论参考和实践指导。

# 关键字
巡线算法；PID控制；性能优化；算法对比；人工智能；传感器融合

参考资源链接：[PID算法控制解析：从比例到积分微分](https://wenku.csdn.net/doc/6412b778be7fbd1778d4a68d?spm=1055.2635.3001.10343)
# 1. 巡线算法的基础知识概述

巡线算法是自动控制系统中的一个重要分支，主要应用于机器人、无人机、自动化生产线等场景，目的是使移动设备能够准确、高效地沿着预设的路径运行。在深入理解各类巡线算法之前，掌握基础知识是至关重要的。

## 1.1 巡线算法的定义和分类

巡线算法是一系列算法的统称，它们通过分析路径上的标志、物理边界或视觉图像来指导设备的移动。根据应用场合和实现原理的不同，巡线算法大致可以分为以下几类：
- 基于传感器的巡线算法
- 视觉识别巡线算法
- 模糊逻辑巡线算法
- 基于人工智能的高级巡线算法

## 1.2 巡线算法的基本要求

无论采用哪种巡线算法，都应满足以下基本要求：
- **准确性**：确保移动设备能够准确地沿着预定路径行驶。
- **鲁棒性**：算法应对环境变化和异常情况具有一定的适应性和容错能力。
- **效率**：算法运行需要高效，以满足实时处理的需求，尤其是在动态变化的环境中。

通过掌握这些基础知识，我们能够为后续章节中对各类具体算法的深入讨论打下坚实的基础。

# 2. PID算法的理论与实践应用

## 2.1 PID算法的基本原理

### 2.1.1 PID控制系统的构成

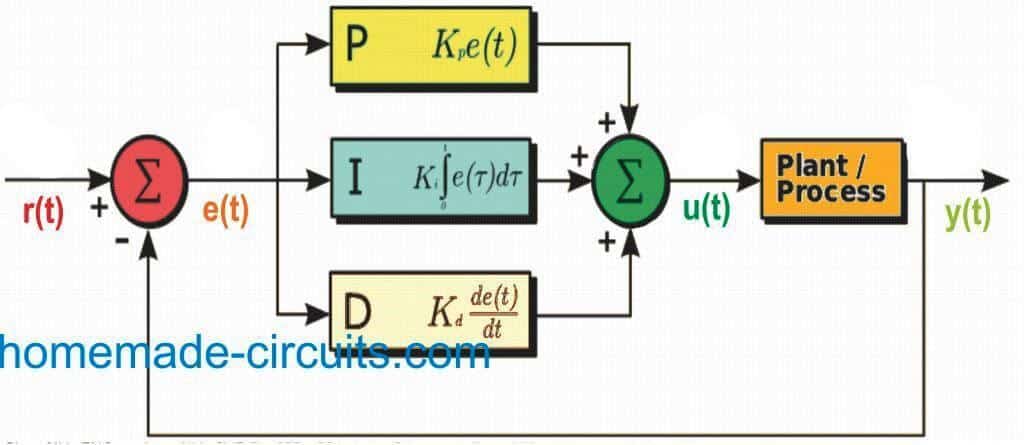
PID控制器是一种常见的反馈控制器，它的名称来自于比例（Proportional）、积分（Integral）、微分（Derivative）三种控制作用的英文首字母缩写。在巡线算法的应用中，PID控制器能够根据偏差的变化，实时调整控制输出，以此来使机器人或自动化设备能够稳定地沿着预定路径移动。

PID控制器的构成可以分为以下几个部分：

- **比例（P）部分**：这一部分的作用是对当前误差进行线性处理，即直接与误差大小成比例。它能够快速减小偏差，但往往不能完全消除稳态误差。
- **积分（I）部分**：这一部分对误差进行累积计算，能够消除稳态误差，但可能会引起系统超调，导致系统响应速度降低。

- **微分（D）部分**：这一部分的作用是对误差变化率进行控制，可以预测未来的误差趋势并进行提前调整，从而减少超调，提高响应速度。

### 2.1.2 PID控制器参数的调整方法

调整PID控制器的参数是实现良好控制性能的关键步骤。下面介绍几种常见的参数调整方法：

- **经验试凑法**：这是最简单直观的方法，根据系统的响应情况进行参数调整。这种方法缺乏理论依据，但便于理解和操作，适合于简单系统。

- **Ziegler-Nichols方法**：这是一种经典的比例调整方法，通过观察系统的临界反应点来确定P、I、D的参数，使系统达到临界稳定状态，并依据经验公式计算出PID的参数值。

- **优化算法**：如遗传算法、粒子群优化等，利用计算机模拟和算法优化技术，可以自动搜索最优的PID参数。这种方法虽然计算量较大，但通常能得到较优的结果。

## 2.2 PID算法的编程实现

### 2.2.1 PID算法的代码结构

在编程实现PID控制器时，通常会按照以下结构进行：

// PID控制器结构体定义
typedef struct {
    double Kp; // 比例增益
    double Ki; // 积分增益
    double Kd; // 微分增益
    double setpoint; // 设定目标值
    double integral; // 积分累计
    double prev_error; // 上一次误差
} PID_Controller;

// PID更新函数
double PID_Update(PID_Controller* pid, double current_value, double dt) {
    double error = pid->setpoint - current_value; // 计算误差
    pid->integral += error * dt; // 更新积分项
    double derivative = (error - pid->prev_error) / dt; // 计算微分项
    double output = pid->Kp * error + pid->Ki * pid->integral + pid->Kd * derivative; // 计算输出
    pid->prev_error = error; // 更新上一次误差
    return output; // 返回控制器输出值
}

### 2.2.2 PID参数调整的实践经验

在实践中，PID参数的调整非常依赖于具体的系统特性，以下是一些调整PID参数的经验性建议：

- **比例增益Kp**：通常首先进行调整，增大Kp会使系统响应更快，但过大会导致系统振荡，应逐步增大Kp直到系统出现微小振荡为止，然后适当减小。

- **积分增益Ki**：在Kp调节好之后进行调整，Ki负责消除稳态误差，但过大的Ki会使系统反应迟钝并引起振荡，需要在不影响系统稳定性的前提下适当提高。

- **微分增益Kd**：最后进行调整，Kd可以提高系统的快速性和稳定性，防止超调，但过大会对噪声过于敏感，应适度增加以避免对噪声过度反应。

## 2.3 PID算法的性能优化与案例分析

### 2.3.1 PID性能优化策略

性能优化是PID算法在实际应用中一个持续的任务。优化策略可以包括：

- **积分饱和防止**：防止积分项过大导致的积分饱和问题，通常会限制积分项的最大值和最小值。

- **微分先行**：在微分项上加入一个系数，即微分先行（Derivative on Measurement），以减少对噪声的敏感度。

- **动态调整策略**：根据系统的不同运行阶段动态调整PID参数，以适应不同的控制需求。

### 2.3.2 实际应用中的案例研究

例如，在自动化巡线机器人中，通过动态调整PID参数来适应不同路面状况：

if (路面状况 == 平滑) {
    // 增加Kp和Ki，减少Kd
    AdjustPIDParameters(&pid, Kp增益, Ki增益, Kd减益);
} else if (路面状况 == 坑洼) {
    // 减少Kp和Ki，增加Kd以减少超调
    AdjustPIDParameters(&pid, Kp减益, Ki减益, Kd增益);
}

此外，对于实际场景中的巡线任务，工程师经常需要结合PID的调整和实际环境变量（如传感器反馈）来优化控制逻辑，使机器能够适应不同的巡线条件。

**注意**：以上代码块与示例均是虚构的，