【深入理解】PID巡线算法的数学模型与仿真技术指南


# 摘要
本论文系统地介绍了PID巡线算法的理论基础、仿真环境搭建、实践应用及未来展望。首先，概述了PID巡线算法的基本原理和要求，以及其在控制系统中的理论应用。接着，详细讨论了如何构建PID巡线算法的数学模型，并对其性能指标和优化策略进行了分析。第三章聚焦于仿真环境的搭建，包括仿真工具的选择、模型创建与调试，以及仿真结果与实际情况的对比。第四章介绍了PID巡线算法在不同场景下的硬件实现、应用案例和性能评估。最后，对PID巡线算法未来的技术趋势和跨学科融合创新进行了展望，分析了当前技术的挑战和发展方向。本文旨在为相关领域的研究者和工程师提供详尽的理论依据和实践经验。

# 关键字
PID巡线算法；数学模型；性能优化；仿真环境；硬件实现；技术趋势

参考资源链接：[PID算法控制解析：从比例到积分微分](https://wenku.csdn.net/doc/6412b778be7fbd1778d4a68d?spm=1055.2635.3001.10343)
# 1. PID巡线算法概述

在自动化控制系统中，巡线算法被广泛应用于各种移动设备中，以实现精确的路径规划和导航。PID（比例-积分-微分）巡线算法是一种经典的控制策略，它通过实时调整机器人的行进方向和速度来实现精准跟踪预定路径。由于其结构简单、易于实现和调整，PID巡线算法在工业领域和科研项目中占据了重要位置。本章将介绍PID巡线算法的基础概念，为后续章节对其深入分析和应用实例的探索奠定基础。

# 2. PID巡线算法的理论基础

## 2.1 巡线算法的原理

### 2.1.1 巡线任务的定义和要求

巡线任务通常是指在一定的路径上使移动机器人或者车辆按照预定的轨迹行驶。在自动巡线系统中，机器人需要自主地识别路径，并根据路径信息进行导航和定位。实现这一过程的关键是巡线算法。此算法需要对环境有较强适应能力，能在各种复杂条件下准确快速地完成巡线任务。

为了完成巡线任务，算法必须满足以下要求：

- **稳定性**：机器人能够保持在预定路径上行驶，不会出现大的偏离。
- **鲁棒性**：在路径出现小的变动或有干扰（如光照变化、地面不平）时，机器人仍能稳定行驶。
- **实时性**：算法能够快速响应环境变化，实时调整行驶方向和速度。
- **简单性**：算法结构不宜过于复杂，以方便在资源受限的硬件上实现。

### 2.1.2 巡线算法中的PID控制理论

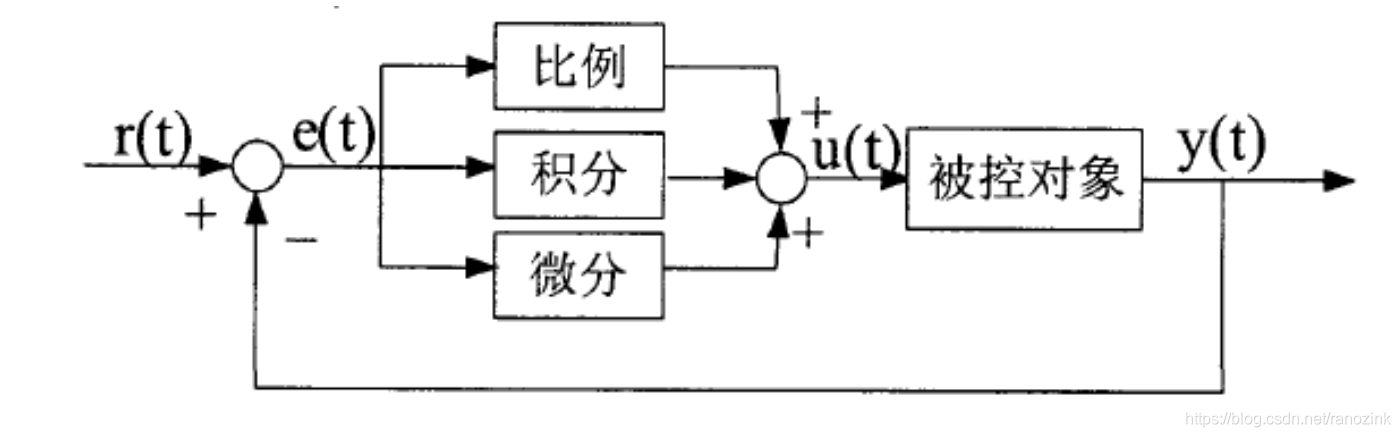
PID控制理论是巡线算法的核心组成部分。PID代表比例（Proportional）、积分（Integral）、微分（Derivative），这些控制环节可以单独或组合使用，以实现对系统输出的精确控制。在巡线算法中，PID控制器根据机器人位置与路径之间的偏差，动态调整机器人的速度和方向，以使机器人准确跟踪预设路径。

- **比例控制（P）**：根据当前偏差大小，调整控制量，偏差大时控制量大。
- **积分控制（I）**：累积偏差，用于消除稳态误差，使系统稳定在目标位置。
- **微分控制（D）**：根据偏差变化速率调整控制量，以抑制快速偏差变化，增加系统的稳定性。

在PID巡线算法中，控制系统通常需要处理多维的输入数据，如直线和曲线路径的检测，以及实际与预设路径的偏差等，PID控制器需要对这些多维数据进行处理，提供合理的控制输出。

## 2.2 数学模型的构建

### 2.2.1 基于传感器数据的模型解析

构建数学模型是实现PID巡线算法的前提。传感器数据的获取和处理对于模型的构建至关重要。常见传感器包括红外传感器、超声波传感器、摄像头等，它们能够感知环境信息并将其转换为电信号供算法处理。在此基础上，可构建传感器数据的数学模型，模型通常包含了数据采集、信号处理和特征提取等环节。

例如，对于红外传感器，可以使用一个简单的阈值法来判断传感器是否检测到线。模型的输出为线的位置信息，这可以作为PID控制器输入的一个关键参数。信号处理可能包括滤波和放大，确保所提取的特征尽可能准确。

### 2.2.2 PID参数与模型关系的分析

在得到传感器数据并构建了数学模型之后，需要确定PID控制器的三个关键参数：比例系数（Kp）、积分系数（Ki）和微分系数（Kd）。这些参数的选取直接影响控制系统的性能，通常通过理论计算、模拟仿真或者实验调整来获得。

- **比例系数Kp**：决定控制量与偏差大小的比例关系，反映系统的反应速度。
- **积分系数Ki**：反映了对累积偏差的响应程度，与消除稳态误差的能力有关。
- **微分系数Kd**：对偏差变化率的响应程度，决定了系统的阻尼特性。

这三个参数的相互影响构成了控制系统的核心。例如，当机器人偏离路径时，比例项会产生一个与偏差成正比的控制量，引导机器人返回路径；积分项负责消除偏差，而微分项则用于预测未来的偏差变化，减少超调和振荡。

## 2.3 算法性能指标与优化

### 2.3.1 性能指标的定义和评价方法

在使用PID算法进行巡线时，定义合适的性能指标至关重要，这些指标反映了算法和整个控制系统的性能。典型的性能指标包括：

- **响应时间**：从系统开始到达到期望状态的时间。
- **稳态误差**：系统稳定后，输出与期望值之间的误差。
- **超调量**：系统输出超过期望值的最大值。
- **调整时间**：系统到达期望状态后，输出在期望值附近波动的时间段。

评价这些性能指标通常涉及实验测量和数据分析。在测量时，可能需要设计特定的测试轨迹来模拟不同的操作条件，收集系统响应数据并进行处理。

### 2.3.2 算法优化策略和实际应用案例

为了提高PID巡线算法的性能，必须采用优化策略调整PID参数。这些策略通常包括：

- **经验法**：基于经验选取PID参数，然后通过试错法逐步调整。
- **Ziegler-Ni