【参数匹配】为您的项目选择最优PID参数的策略


# 摘要
PID控制器是控制系统中最常用的调节器之一，它通过比例（P）、积分（I）和微分（D）三个参数的作用来实现对系统的精确控制。本文首先介绍了PID控制器的基本原理及作用，随后详细解读了各个PID参数的定义、功能及它们对系统稳定性的影响。文章第三章聚焦于PID参数的选择与调整，探讨了如Ziegler-Nichols方法和软件辅助工具等实用调整技术。第四章通过不同领域的应用案例，展现了PID参数匹配的实际效果和适应性。第五章展望了PID控制器未来的发展趋势，包括鲁棒PID设计和基于机器学习的参数自适应技术。本文旨在综合理论与实践，为控制工程领域的研究者和工程师提供全面的参考。

# 关键字
PID控制器；控制系统；参数调整；稳定性分析；自适应技术；鲁棒控制

参考资源链接：[PID算法控制解析：从比例到积分微分](https://wenku.csdn.net/doc/6412b778be7fbd1778d4a68d?spm=1055.2635.3001.10343)
# 1. PID控制器的基本原理和作用

PID控制器（比例-积分-微分控制器）是工业自动化控制领域中最常见的反馈控制器。其核心思想在于不断测量和比较系统输出与期望值之间的差距，通过计算并输出一个修正值以调整系统的行为，从而达到控制的目的。

## PID控制器的基本组成

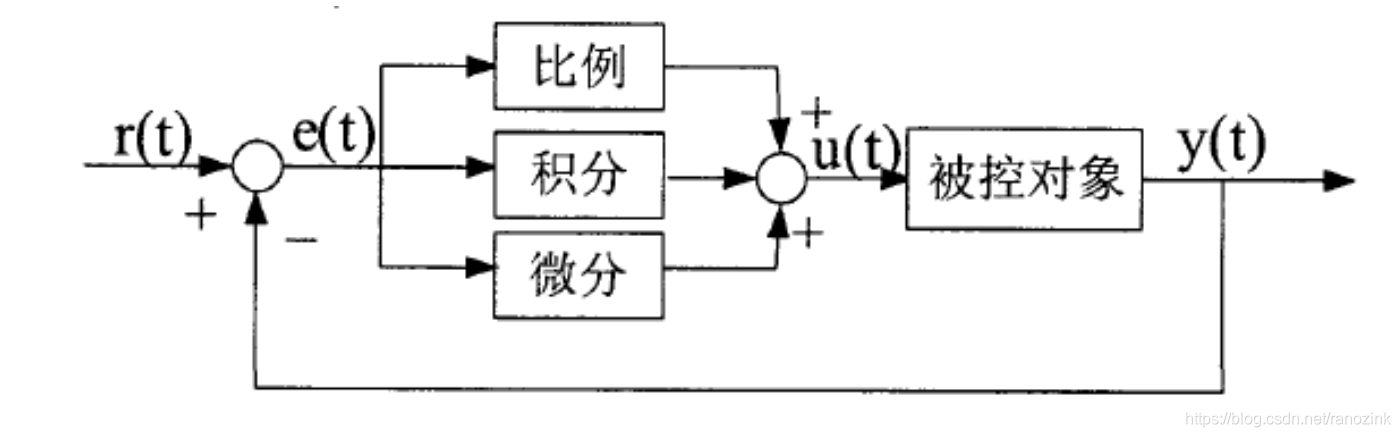
PID控制器由比例、积分和微分三个主要部分构成，它们共同作用以减少偏差并稳定系统。

- **比例（Proportional）**：根据当前偏差大小进行控制，偏差越大，控制作用越强。但单纯的比例控制会导致稳态误差。
- **积分（Integral）**：积分作用是为了消除稳态误差。它对过去一段时间内的偏差进行累积并作出反应，使系统输出达到期望值。
- **微分（Derivative）**：微分作用反映了偏差的变化趋势，其目的是预测未来偏差并提前作出调整，提高系统的响应速度和稳定性。

## PID控制器的作用

- **实现精确控制**：PID通过不断调整输出，确保系统的输出能紧跟目标设定值，实现精准控制。
- **减少稳态误差**：积分项的加入有效减少或消除长时间累积的偏差。
- **增强系统的稳定性**：微分项可以帮助系统更快速地响应变化，减少超调和振荡，提高稳定性和响应速度。

通过结合这三部分，PID控制器可以广泛应用于各种控制系统中，如温度控制、流量控制、速度控制等，以达到优化控制性能的目的。在后续章节中，我们将深入探讨PID参数的详细调整与应用。

# 2. 理论基础——PID参数详解

在探索PID（比例-积分-微分）控制器的奥秘时，理解其核心构成是至关重要的。每个参数都有其独特的角色和影响，它们的互动决定了系统的响应特性和稳定性。深入探讨PID参数的定义、功能、与系统稳定性之间的关系，以及调整方法，是掌握PID控制器应用的关键。

## 2.1 PID参数的定义与功能

### 2.1.1 比例（P）的作用与影响
比例部分负责响应当前误差，即设定点与实际输出之间的差异。P参数越大，控制器对误差的反应就越强烈，可以快速减少误差。但是，如果P值过高，系统可能会产生过冲甚至不稳定。

**代码示例与分析：**

# 伪代码展示P控制器行为
def p_controller(setpoint, measured_value, Kp):
    error = setpoint - measured_value
    output = Kp * error  # P控制器输出
    return output

在这个例子中，`Kp`代表比例增益，其值越大，控制器的反应越快，输出的变化也越剧烈。然而，如果`Kp`太大，可能会引起系统的振荡。

### 2.1.2 积分（I）的作用与影响
积分部分关注的是误差随时间的累积。它使控制器能够消除稳态误差，即在长期运行中，如果存在任何持续的误差，积分项会使输出逐渐调整以抵消这个误差。不过，积分作用太强可能会导致系统反应迟缓，增加超调的风险。

**代码示例与分析：**

# 伪代码展示PI控制器行为
def pi_controller(setpoint, measured_value, Kp, Ki, integral):
    error = setpoint - measured_value
    integral += error  # 更新积分项
    output = Kp * error + Ki * integral  # PI控制器输出
    return output, integral

在这个代码示例中，`Ki`是积分增益，通过累加误差来计算输出。积分项`integral`的值会随着时间逐渐累积，帮助消除稳态误差。

### 2.1.3 微分（D）的作用与影响
微分部分是对误差变化率的响应，它预测误差的趋势并作出调整以避免过冲。微分控制使系统能够快速响应变化，有助于减少超调和振荡，但过强的微分作用可能会放大噪声。

**代码示例与分析：**

# 伪代码展示PD控制器行为
def pd_controller(setpoint, measured_value, Kp, Kd, previous_error):
    error = setpoint - measured_value
    derivative = error - previous_error  # 计算误差变化率
    output = Kp * error + Kd * derivative  # PD控制器输出
    return output

在该示例中，`Kd`是微分增益，用于计算误差变化率。通过引入微分项`derivative`，控制器能够对误差的变化趋势做出反应，从而提高系统的稳定性和减少过冲。

## 2.2 PID参数与系统稳定性的关系

### 2.2.1 系统稳定性的基本概念
稳定性是控制系统设计的首要目标之一，指的是系统在受到扰动后能够回到或保持在期望的操作状态。稳定性分析对于确保控制器参数能够提供预期的系统行为至关重要。

### 2.2.2 PID参数对稳定性的调节
适当的PID参数设置对于保持系统的稳定至关重要。P参数负责快速响应，I参数负责消除稳态误差，D参数则增强系统的抗振荡能力。只有恰当地平衡这三个参数，系统才能表现出良好的稳定性和性能。

## 2.3 PID参数的调整方法

### 2.3.1 手动调整法
手动调整PID参数是一个迭代的过程，通常根据经验和系统响应来逐步调整参数。这种方法需要操作者具有深厚的工程知识和理解能力，以识别和分析系统行为。

### 2.3.2 自动调整法和先进算法
自动调整法，如Ziegler-Nichols方法，提供了一种系统化的方法来确定PID参数。此外，还有基于模型的调整方法和使用先进算法如遗传算法、粒子群优化等智能优化方法来自动寻找最佳的PID参数。

PID控制器参数的深入解析为理解和应用PID控制提供了坚实的理论基础，而接下来的章节，我们将通过实践案例来探讨如何在实际应用中进行参数的选择与调整。

# 3. 实践操作——PID参数的选择与调整

在现代工业自动化中，PID控制器的性能优化是一项至关重要的任务，其核心在于正确选择和调整PID参数。本章将深入探讨如何通过Ziegler-Nichols方法以及软件工具来进行PID参数的匹配与调整，并介绍如何进行参数的微调与优化。

## 使用Ziegler-Nichols方法确定PID参数

### 开环法的基本步骤和实例

Ziegler-Nichols开环法是一种简单且直观的方法，用于初步确定PID控制器的参数。这种方法不需要系统进入闭环状态，适合于那些不希望或无法轻易中断生产过程的场合。

#### 基本步骤：

1. 在控制回路中移除或去激活PID控制器。
2. 将控制器输出直接连接到执行机构（例如，电机驱动器）。
3. 记录系统对于一个阶跃输入响应的数据。
4. 使用这些响应数据来计算PID参数。

**实例：**

假设一个温度控制系统对阶跃输入有一个响应曲线如下：

1. 首先记录系统的最终稳态值和达到最终值的时间。
2. 使用这些数据，我们可以通过Ziegler-Nichols提供的经验公式计算出P、I、D三个参数。

- 比例带宽（P）：100%
- 积分时间（I）：1.5倍达到最终稳态的时间
- 微分时间（D）：0.5倍达到最终稳态的时间

### 闭环法的基本步骤和实例

与开环法相比，闭环法适用于已经可以运行在闭环状态的系统。它通过逐渐增加控制器的增益，直到系统出现持续振荡为止。

#### 基本步骤：

1. 将控制器设置为仅比例控制。
2. 逐渐增加比例增益，直到输出出现持续振荡。
3. 记录此时的比例增益（Ku）和振荡周期（Pu）。
4. 根据Ziegler-Nichols提供的公式计算