程序员面试算法思维拓展：回溯算法与位运算技巧


# 摘要
本文旨在深入探讨面试算法思维，并详细解析回溯算法与位运算的理论基础及其应用技巧。首先概述了面试中算法思维的重要性，随后详细介绍回溯算法的工作原理、关键步骤及典型应用案例，如解决N皇后问题和组合问题。接着，本文转向位运算，阐述其基础知识、在算法中的应用以及优化算法性能的高级技巧。最后，结合实际面试场景，分析了回溯算法与位运算的结合应用，并提供实践演练和拓展提升的策略。通过本文的学习，读者将能更好地掌握算法面试的必备知识，提高解决复杂算法问题的能力。

# 关键字
面试算法思维；回溯算法；位运算；状态空间树；剪枝策略；复杂度优化

参考资源链接：[程序员面试必备：实用算法集锦](https://wenku.csdn.net/doc/2b9k9b8gkc?spm=1055.2635.3001.10343)
# 1. 面试算法思维概览

在当今竞争激烈的IT行业，面试中的算法题目已成为许多企业评估候选人技术能力的一个重要环节。面试算法思维不仅要求求职者掌握各种算法知识和编程技巧，更重要的是培养一种系统化、逻辑性强的解题思维方式。本章将为读者提供算法面试的全面概览，帮助读者搭建起应对面试中可能出现算法问题的思维框架。

面试者必须意识到算法不仅仅是一门技术，更是一种解决复杂问题的策略。算法思维的培养包括理解问题本质、设计高效解决方案、优化算法性能等方面。本章将简单介绍面试中常见的算法题型，如动态规划、图论、排序等，并给出策略性的思考方法，为读者提供实战前的理论基础。

## 1.1 算法面试的目的与意义

算法面试的目的是通过一系列问题来考察候选人的逻辑思维能力、编程技能和问题解决能力。在这个过程中，面试官不仅评估候选人对特定算法的掌握程度，还要考察他们如何将理论应用到实际问题中，以及在压力下思考问题的能力。一个算法思维清晰的求职者能够准确把握问题的关键点，并迅速提出可行的解决方案。

## 1.2 面试算法的类型与特点

在面试中，算法题目的类型往往多种多样，常见的有数组和字符串操作、链表和树的处理、图的遍历等。每一种题型都有其特定的解题策略和技巧。例如，数组和字符串问题经常利用双指针或滑动窗口来解决；树和图的问题则需要运用递归或图算法来处理。了解并掌握这些题型和策略是面试成功的关键。

## 1.3 面试准备与实践建议

准备面试算法题不仅需要理论知识，更需要大量的实践。建议求职者通过在线编程平台进行实战训练，如LeetCode、HackerRank等，这些平台提供了丰富的题目和模拟面试环境。同时，理解算法时间复杂度和空间复杂度对于评估算法的效率至关重要，因此也应成为面试准备的重要部分。

在后续章节中，我们将深入探讨回溯算法、位运算等具体算法及其在实际面试中的应用，以及如何在实战中提升算法思维，进阶为一个更加高效的IT行业从业者。

# 2. 回溯算法的理论与实现

### 2.1 回溯算法的原理与特点

#### 2.1.1 回溯算法的定义与作用

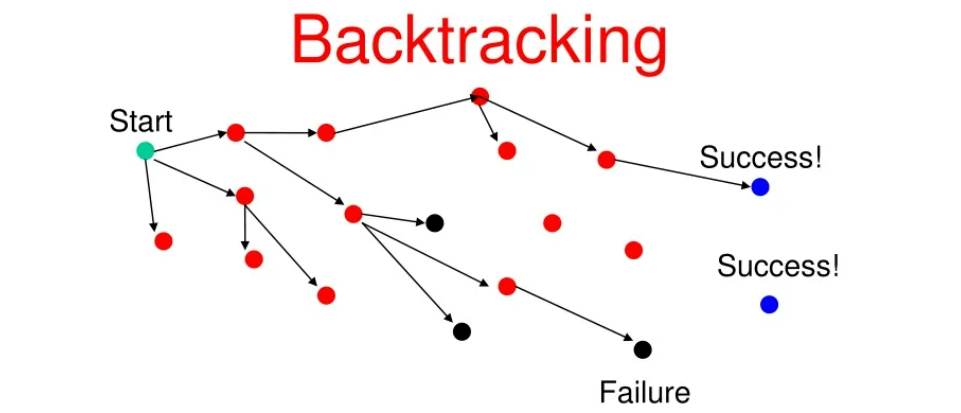
回溯算法是一种通过探索所有潜在可能性来找出所有解的算法，如果发现当前解不可能是最后的答案，就回退到上一步继续尝试其他选项。这种方法类似于深度优先搜索，但更注重于在解空间树上的搜索过程，并在不合适的情况下及时回溯。

回溯算法的典型应用场景是组合问题，如子集问题、排列问题和组合问题。在设计问题解决方案时，它可以帮助我们构建出所有可能的候选解，并通过剪枝来避免无效搜索，提高效率。

#### 2.1.2 回溯算法与递归的关系

回溯算法与递归之间存在着密切的关系。由于回溯的本质是尝试和撤销的过程，递归成为实现这一过程的自然选择。递归函数能够保持状态，易于表示算法的递归结构，而且在回溯点可以直接返回到上一个状态。

在回溯算法的实现中，递归函数通常用于遍历解空间树的每一个节点，当发现当前路径不可能达到有效解时，递归函数将返回上一级，也就是回溯到父节点，继续尝试其它分支。

### 2.2 回溯算法的关键步骤详解

#### 2.2.1 状态空间树的构建

状态空间树是一种用于表示所有可能状态及其之间关系的树形结构。在回溯算法中，树的每一个节点代表问题的一个状态，节点之间的边代表从一个状态到另一个状态的转换。

构建状态空间树是回溯算法的第一步，它需要根据问题的特性设计节点以及节点之间的转换规则。以N皇后问题为例，每个节点代表放置一个皇后的位置，边代表皇后位置之间的合法移动。

#### 2.2.2 路径与决策点分析

在状态空间树中，路径表示从树的根节点到任意一个节点的路径，每个路径上的节点表示了到达该节点时所有变量的一个可能取值。决策点是路径上的每一个节点，它需要做出选择来决定是否继续延伸路径或回溯。

在实现回溯算法时，每个决策点都对应着一个递归调用。通过递归函数的参数传递当前的状态信息，并在每次递归调用时更新这些状态信息。

#### 2.2.3 剪枝策略的应用

剪枝策略是回溯算法中提高效率的关键，它指的是在搜索过程中，当某个节点不可能产生最优解时，就停止继续探索这一分支。剪枝可以减少不必要的搜索空间，从而提高算法的运行效率。

应用剪枝策略时，通常需要在算法中添加一些判断逻辑。例如，在N皇后问题中，当我们确定一行只能放置一个皇后时，如果某一列已经有了皇后，那么后续的该列上的行则无需考虑。

### 2.3 回溯算法的典型应用案例

#### 2.3.1 N皇后问题的回溯解法

N皇后问题要求在N×N的棋盘上放置N个皇后，使得它们互不攻击，即任意两个皇后都不在同一行、同一列及同一对角线上。

解决N皇后问题的回溯算法一般从第一行的第一列开始尝试放置皇后，然后递归地在下一行尝试放置另一个皇后，并检查是否安全。若当前放置不合法，则回溯到上一个皇后的位置，尝试其他列，直到所有皇后都放置完成。

def solve_n_queens(n):
    def is_safe(board, row, col):
        # 检查列冲突
        for i in range(row):
            if board[i] == col or \
               board[i] - i == col - row or \
               board[i] + i == col + row:
                return False
        return True

    def solve(board, row):
        if row == n:
            result.append(board[:])
            return
        for col in range(n):
            if is_safe(board, row, col):
                board[row] = col
                solve(board, row + 1)
                board[row] = -1
    result = []
    solve([-1] * n, 0)
    return result

# 输出所有解
for solution in solve_n_queens(4):
    for row in solution