【性能评估深入解析】：准确度、召回率与F1分数精讲

# 1. 性能评估指标概述

性能评估是衡量算法、模型或系统效能的关键环节。了解和应用正确的评估指标可以有效指导我们的开发和优化工作。评估指标通常涉及准确度、召回率、精确率、F1分数等多个维度，它们分别衡量模型在不同方面的表现。准确度关注于预测正确的样本数占总样本数的比例，是最直观的性能度量。而召回率衡量的是模型对正类样本的识别能力，它关注于模型捕获正类样本的完整度。在处理各类实际问题时，平衡准确度与召回率是一个永恒的挑战，尤其在正负样本极度不平衡的情况下更是如此。本章旨在为你构建性能评估指标的基础框架，并为后续章节中更深入的讨论奠定基础。

# 2. 准确度与召回率的基本概念

### 2.1 准确度的定义与计算方法

#### 理解准确度的含义

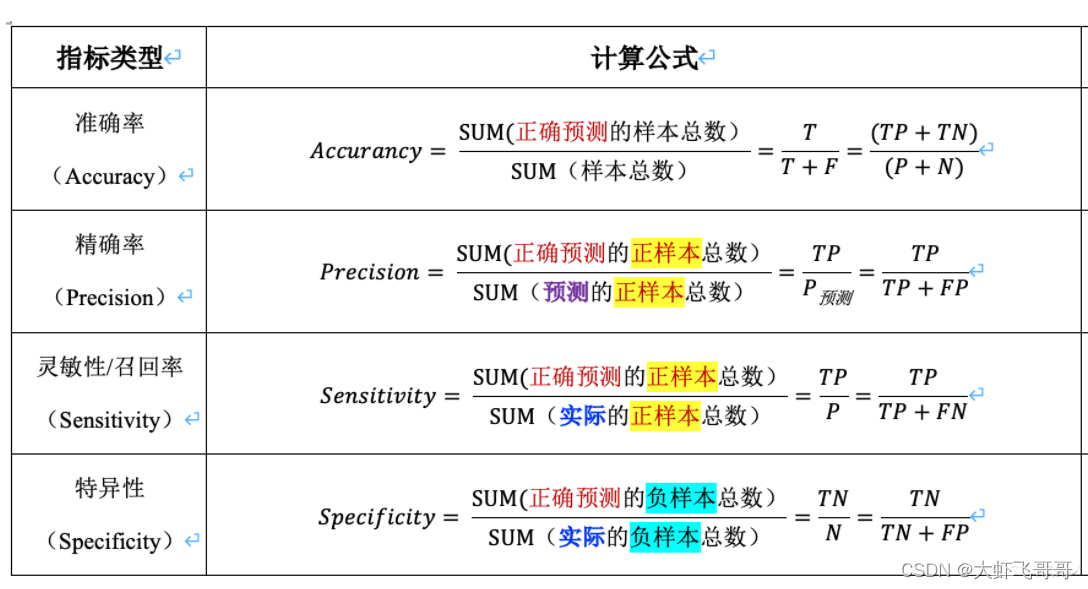
准确度（Accuracy）是衡量分类模型预测结果与实际结果一致性的最直观指标。它表示了在所有预测结果中，有多少比例是正确的。准确度的概念简单，易于理解，它直接反映了模型的预测性能。在实际应用中，准确度往往是一个重要的评估标准，尤其是在样本类别分布相对均衡的数据集上。

#### 准确度的计算公式及其应用

准确度的计算公式为：

准确度 = (真正例 + 真负例) / 总样本数

在实际应用中，准确度的计算过程需要根据模型的预测结果和实际标签进行。具体步骤如下：

1. 预测模型对测试数据集中的每个样本进行分类。
2. 将预测结果与实际标签进行比较，统计真正例（TP）、真负例（TN）、假正例（FP）和假负例（FN）的数量。
3. 应用公式计算准确度。

在特定业务场景下，例如欺诈检测或者疾病诊断，准确度的高低直接关联到业务成本的高低。高准确度意味着模型在实际应用中能更有效地减少错误判断所带来的损失。

### 2.2 召回率的定义与计算方法

#### 理解召回率的含义

召回率（Recall）又称为“真正类率”（True Positive Rate, TPR），它度量的是实际为正类的样本中有多少比例被模型正确识别出来。召回率关注于模型对正类的识别能力，尤其在正类样本较少的情况下，召回率是一个重要的衡量指标。

#### 召回率的计算公式及其应用

召回率的计算公式为：

召回率 = 真正例 / (真正例 + 假负例)

在计算召回率时，同样需要统计真正例和假负例的数量。计算过程如下：

1. 继续使用准确度计算时的TP、TN、FP、FN值。
2. 应用公式计算召回率。

召回率在一些领域尤其重要，如医疗诊断，宁可错判也不可漏判，召回率的高低直接关联到患者的健康甚至生命安全。

### 2.3 准确度与召回率的关系

#### 两者之间的平衡问题

准确度和召回率是一对典型的评价指标权衡关系，在实际应用中，这两个指标往往很难同时达到最优。提高准确度可能会以牺牲召回率为代价，反之亦然。这种关系常被称为“准确度-召回率权衡”（Accuracy-Recall Trade-off）。

#### 实际案例分析

在实际应用中，例如垃圾邮件检测系统，开发者需要决定是优化模型以减少将正常邮件误判为垃圾邮件（假正例），还是减少将垃圾邮件误判为正常邮件（假负例）的风险。通常情况下，前者可能更为用户所接受，因为用户可能不愿意错过任何一封重要邮件，这就需要降低假负例，提高召回率。

通过下面的例子，可以更直观地理解这种平衡：

假设有一个垃圾邮件识别器，准确度为90%，召回率为80%。这意味着在所有邮件中，90%被正确识别，但在所有实际的垃圾邮件中，只有80%被系统识别出来。如果我们将准确度提升至95%，有可能会因为过于严格的条件而导致召回率下降，比如降低至70%。这时，虽然有更多邮件被正确识别，但漏掉的垃圾邮件比例也更高了。

在这种平衡中，业务需求将决定最终的优化方向。对于不同的业务场景，决策者需要根据实际需求来权衡这两个指标。

# 3. F1分数的理论与应用

## 3.1 F1分数的数学定义

### 3.1.1 F1分数的计算公式

F1分数是精确率（Precision）和召回率（Recall）的调和平均数，它提供了一个单一的指标来平衡这两个指标。F1分数的计算公式如下：

\[ F1 = 2 \times \frac{\text{精确率} \times \text{召回率}}{\text{精确率} + \text{召回率}} \]

其中，精确率是指所有被认为是正类的实例中，实际为正类的比例；召回率是指所有实际为正类的实例中，被正确识别为正类的比例。F1分数的值介于0到1之间，1表示完美匹配，0表示完全没有匹配。

### 3.1.2 F1分数的意义及其与其他指标的比较

F1分数特别适用于那些精确率和召回率同等重要的分类任务。相比于单独使用精确率或召回率，F1分数更能够提供对模型性能的全面评价。例如，在医疗诊断中，既希望尽可能多地识别出真正的病人（高的召回率），又不希望将健康人错误地诊断为病人（高的精确率），这时F1分数就是一个很好的选择。

与常用的其他性能指标相比，如准确率（Accuracy），F1分数能够更好地处理类别不平衡的数据集。在类别不平衡的情况下，准确率可能会因为多数类的影响而产生误导性的高值，而F1分数则能更真实地反映模型的性能。

## 3.2 F1分数的计算实例

### 3.2.1 不同场景下的F1分数计算

假设我们有一个二分类问题的数据集，其中一个类别非常罕见（比如只占1%）。如果一个模型简单地预测所有的实例都是多数类，它的准确率可能会非常高（比如99%），但是这种模型实际上是没有任何用处的，因为它没有正确识别出任何少数类实例。

为了更真实地评估模型性能，我们可以使用精确率和召回率，并结合F1分数。例如，如果模型在某个测试集上的精确率为70%，召回率为60%，那么F1分数计算如下：

\[ F1 = 2 \times \frac{0.7 \times 0.6}{0.7 + 0.6} = 0.643 \]

### 3.2.2 F1分数在多类分类问题中的应用

在多类分类问题中，我们可以为每一个类别计算一个F1分数，然后取所有类别的F1分数的平均值作为模型整体性能的评估指标。也可以选择加权平均，给那些更重要的类别更高的权重。

例如，在一个多类分类问题中，如果一个模型对于三个类别的精确率和召回率分别为：

- 类别1：精确率=0.8，召回率=0.9
- 类别2：精确率=0.7，召回率=0.8
- 类别3：精确率=0.9，召回率=0.6

对应的F1分数分别为：

\[ F1_1 = 2 \times \frac{0.8 \times 0.9}{0.8 + 0.9} = 0.846 \]
\[ F1_2 = 2 \times \frac{0.7 \times 0.8}{0.7 + 0.8} = 0.743 \]
\[ F1_3 = 2 \times \frac{0.9 \times 0.6}{0.9 + 0.6} = 0.706 \]

如果我们简单地计算平均值：

\[ F1_{\text{avg}} = \frac{0.846 + 0.743 + 0.706}{3} = 0.765 \]

或者，如果我们知道类别1更重要，应该赋予更高的权重：

\[ F1_{\text{weighted}} = \frac{2 \times 0.846 + 1 \times 0.743 + 1 \times 0.706}{4} = 0.774 \]

我们可以看到加权平均的结果略高于简单平均，反映了类别1的重要性。

## 3.3 F1分数的优势与局限性

### 3.3.1 F1分数在实际问题中的优势

F1分数提供了一种平衡精确率和召回率的方法。在许多实际问题中，尤其是那些错误分类成本相似的情况下，F1分数是一个很好的评价指标。它尤其适用于那些数据分布不均的数据集，因为它不像准确率那样容易受到类别不平衡的影响。

### 3.3.2 F1分数无法解决的问题及其应对策略

F1分数不能区分模型在精确率和召回率上的不同偏好。例如，在一些应用中，我们可能更倾向