MATLAB滤波器设计中的因果关系：理解滤波器输入和输出的关系，优化信号处理流程

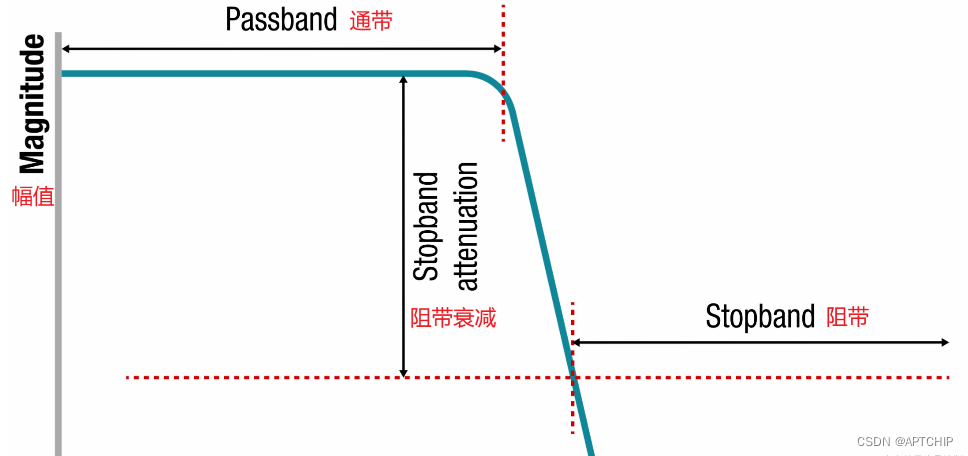
# 1. 滤波器基础

滤波器是一种处理信号的设备或算法，用于去除不想要的频率分量，同时保留所需的频率分量。在MATLAB中，滤波器设计是一个重要的工具，可用于各种信号处理应用。

滤波器通常分为两大类：因果滤波器和非因果滤波器。因果滤波器仅使用当前和过去的输入信号值来计算输出，而非因果滤波器还可以使用未来的输入信号值。因果滤波器在实时应用中至关重要，因为它们不会引入时延。

# 2. 因果滤波器**

因果滤波器是指输出仅依赖于当前和过去输入的滤波器。在信号处理和控制系统中，因果滤波器具有广泛的应用，因为它可以确保系统的稳定性和可实现性。

**2.1 FIR滤波器**

**2.1.1 FIR滤波器的特性**

FIR（有限脉冲响应）滤波器是一种因果滤波器，其输出仅依赖于有限数量的过去输入。FIR滤波器的主要特性包括：

- 线性相位：FIR滤波器的相位响应与频率成线性关系，这对于保持信号波形的形状至关重要。
- 稳定性：FIR滤波器总是稳定的，因为它们的极点都位于单位圆外。
- 易于实现：FIR滤波器可以使用移位寄存器和乘法器轻松实现。

**2.1.2 FIR滤波器设计方法**

FIR滤波器可以通过以下方法设计：

- 窗函数法：使用预定义的窗函数（例如矩形窗、汉明窗）来加权理想频率响应。
- 最小二乘法：最小化滤波器输出与理想输出之间的误差。
- Parks-McClellan算法：使用迭代算法优化滤波器的幅度响应。

**2.2 IIR滤波器**

**2.2.1 IIR滤波器的特性**

IIR（无限脉冲响应）滤波器是一种因果滤波器，其输出不仅依赖于当前和过去输入，还依赖于过去输出。IIR滤波器的主要特性包括：

- 陡峭的截止频率：IIR滤波器可以实现比FIR滤波器更陡峭的截止频率。
- 节省内存：IIR滤波器通常比FIR滤波器需要更少的内存，因为它们只需要存储几个状态变量。
- 潜在的不稳定性：IIR滤波器可能不稳定，因此在设计时需要仔细考虑。

**2.2.2 IIR滤波器设计方法**

IIR滤波器可以通过以下方法设计：

- 双二次滤波器：使用一阶和二阶滤波器的级联来实现复杂的频率响应。
- 巴特沃斯滤波器：使用巴特沃斯多项式来实现平坦的通带和单调的阻带。
- 切比雪夫滤波器：使用切比雪夫多项式来实现更陡峭的截止频率，但代价是通带中的涟漪。

**代码示例：**

% 设计一个 FIR 低通滤波器
order = 100;  % 滤波器阶数
cutoffFreq = 0.2;  % 截止频率（归一化）
window = 'hamming';  % 窗函数

firFilter = designfilt('lowpassfir', 'Order', order, 'CutoffFrequency', cutoffFreq, 'Window', window);

% 设计一个 IIR 巴特沃斯低通滤波器
order = 5;  % 滤波器阶数
cutoffFreq = 0.2;  % 截止频率（归一化）

iirFilter = designfilt('lowpassiir', 'Order', order, 'CutoffFrequency', cutoffFreq, 'FilterType', 'butter');

**逻辑分析：**

上述代码示例展示了如何使用 MATLAB 设计 FIR 和 IIR 低通滤波器。`designfilt` 函数用于指定滤波器的类型、阶数、截止频率和窗口（对于 FIR 滤波器）。

**参数说明：**

- `Order`：滤波器的阶数。
- `CutoffFrequency`：滤波器的截止频率（归一化）。
- `Window`：FIR 滤波器的窗函数。
- `FilterType`：IIR 滤波器的类型（例如，`butter`、`cheby1`）。

# 3. 因果关系在滤波器设计中的应用**

因果关系在滤波器设计中扮演着至关重要的角色，它影响着滤波器的稳定性、时延和组设计。本章将深入探讨因果关系在滤波器设