MATLAB滤波器设计中的频率响应分析：深入理解滤波器特性，优化信号处理

# 1. MATLAB滤波器设计基础

MATLAB是一种强大的技术计算环境，它提供了广泛的工具和函数，用于设计和分析滤波器。滤波器是信号处理中必不可少的工具，用于从信号中去除不需要的成分或增强所需的成分。

MATLAB中滤波器设计的基础包括理解滤波器的基本类型（例如，低通、高通、带通和带阻），以及它们在信号处理中的作用。此外，还涉及滤波器设计参数（例如，截止频率、通带增益和阻带衰减）以及它们如何影响滤波器的性能。

# 2. 滤波器频率响应分析理论

### 2.1 频率响应的定义和重要性

**频率响应**描述了滤波器在不同频率下的幅度和相位响应。它提供了滤波器如何影响信号中不同频率分量的信息。

频率响应对于滤波器设计至关重要，因为它允许工程师根据特定应用的需求调整滤波器特性。通过分析频率响应，可以确定滤波器的截止频率、通带增益和阻带衰减等关键参数。

### 2.2 滤波器频率响应的类型和特性

滤波器频率响应可以分为以下几种类型：

- **低通滤波器：**允许低频分量通过，而衰减高频分量。
- **高通滤波器：**允许高频分量通过，而衰减低频分量。
- **带通滤波器：**允许特定频率范围内的分量通过，而衰减其他频率分量。
- **带阻滤波器：**衰减特定频率范围内的分量，而允许其他频率分量通过。

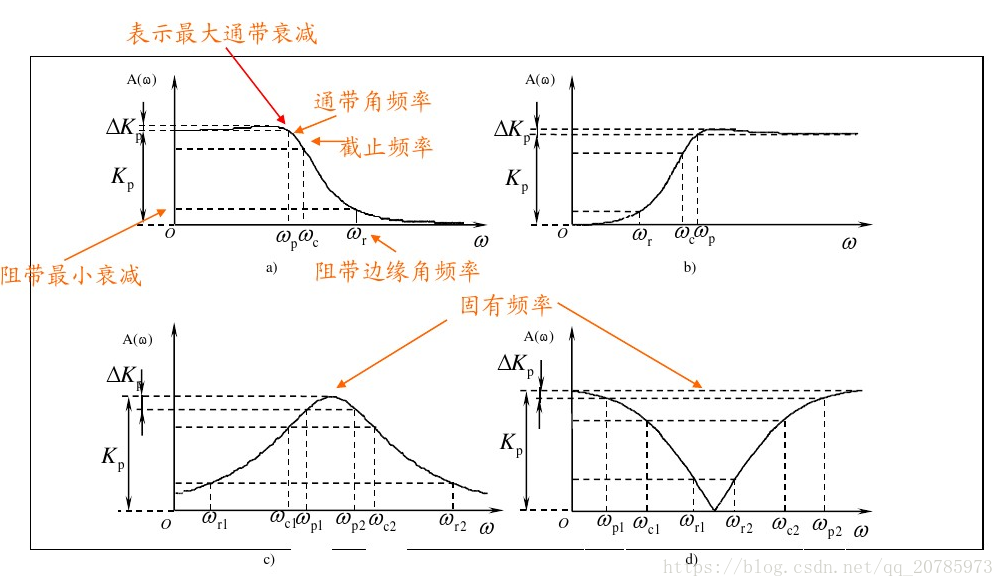
每个滤波器类型的频率响应曲线具有不同的形状和特性。例如，低通滤波器的频率响应曲线在截止频率处急剧下降，而带通滤波器的频率响应曲线在通带内平坦，在通带外衰减。

### 2.3 频率响应分析的常用方法

有几种常用的方法可以分析滤波器的频率响应：

- **波德图：**以对数坐标绘制幅度和相位响应，提供滤波器频率响应的整体视图。
- **奈奎斯特图：**以复平面绘制幅度和相位响应，提供滤波器稳定性和性能的信息。
- **极点零点图：**以复平面绘制滤波器的极点和零点，提供滤波器频率响应的深入理解。

这些方法各有优缺点，选择哪种方法取决于具体应用和所需的分析级别。

# 3. MATLAB滤波器频率响应分析实践

### 3.1 使用MATLAB设计和实现滤波器

**FIR滤波器设计**

MATLAB提供了`fir1`函数用于设计有限脉冲响应(FIR)滤波器。该函数接受以下参数：

- `N`：滤波器阶数（抽头数）
- `Wn`：归一化截止频率（0到1之间）
- `ftype`：滤波器类型（'low'、'high'、'bandpass'、'bandstop'）
- `window`：窗函数类型（'rectwin'、'hamming'、'hann'等）

**IIR滤波器设计**

MATLAB提供了`butter`、`cheby1`和`cheby2`函数用于设计无限脉冲响应(IIR)滤波器。这些函数接受以下参数：

- `N`：滤波器阶数
- `Wn`：归一化截止频率（0到1之间）
- `ftype`：滤波器类型（'low'、'high'、'bandpass'、'bandstop'）
- `Rp`：通带纹波（对于切比雪夫滤波器）
- `Rs`：阻带衰减（对于切比雪夫滤波器）

**滤波器实现**

设计滤波器后，可以使用`filter`函数将其应用于信号。该函数接受以下参数：

- `b`：滤波器系数（分子）
- `a`：滤波器系数（分母）
- `x`：输入信号

**代码示例：**

% 设计一个阶数为100的低通FIR滤波器，截止频率为0.2
b = fir1(100, 0.2);

% 设计一个阶数为10的低通IIR巴特沃斯滤波器，截止频率为0.3
[b, a] = butter(10, 0.3, 'low');

% 将滤波器应用于信号
y = filter(b, a, x);

### 3.2 频率响应分析的MATLAB函数和工具

MATLAB提供了以下函数和工具用于分析滤波器的频率响应：

- `freqz`：绘制滤波器的幅度和相位响应
- `bode`：绘制滤波器的幅度和相位响应（对数刻度）
- `nyquist`：绘制滤波器的奈奎斯特图
- `fvtool`：一个交互式工具，用于可视化和分析滤波器的频率响应

**代码示例：**

% 绘制低通FIR滤波器的频率响应
freqz(b, 1);

% 绘制低通IIR巴特沃斯滤波器的幅度响应
bode(b, a);

% 绘制低通IIR巴特沃斯滤波器的奈奎斯特图
nyquist(b, a);

% 使用fvtool可视化低通IIR巴特沃斯滤波器的频率响应
fvtool(b, a);

### 3.3 滤波器频率响应分析的实例和应用

**实例：**

使用MATLAB设计和分析一个带通滤波器，以提取语音信号中的特定频率成分。

**应用：**

- 信号去噪
- 信号特征提取
- 信号处理算法性能评估

# 4. 滤波器频率响应分析的优化

### 4.1 频率响应优化目标和方法

滤波器频率响应优化旨在通过调整滤波器参数来改善其频率响应特性，以满足特定应用需求。常见的优化目标包括：

- **通带增益优化：**最大化滤波器在通带内的增益，以增强信号幅度。
- **截止频率优化：**调整滤波器截止频率，以精确地分离所需信号和噪声。
- **阻带衰减优化：**最小化滤波器在阻带内的衰减，以抑制不需要的频率分量。
- **相位响应优化：**调整滤波器相位响应，以补偿信号处理系统中的延迟或失真。

优化方法通常涉及使用迭代算法，例如梯度下降或遗传算法。这些算法通过逐步调整滤波器参数来最小化目标函数，该函数衡量频率响应与所需特性的偏差。

### 4.2 滤波器参数调整和优化算法

滤波器参数调整是频率响应优化过程的关键部分。常见的可调参数包括：

- **滤波器阶数：**滤波器的阶数决定其频率响应的陡度和选择性。
- **截止频率：**截止频率定义滤波器通带和阻带之间的分界线。
- **通带增益：**通带增益控制滤波器在通带内的幅度响应。
- **阻带衰减：**阻带衰减控制滤波器在阻带内的衰减量。

优化算法利用这些参数调整来搜索滤波器参数空间，寻找最佳配置。常用的优化算法包括：

- **梯度下降：**一种迭代算法，沿目标函数梯度的负方向移动，以找到局部最小值。
- **遗传算法：**一种基于自然选择原理的启发式算法，通过交叉和突变操作进化滤波器参数。
- **粒子群优化：**一种基于群体智能的算法，其中粒子在参数空间中移动并交换信息，以找到最优解。

### 4.3 滤波器频率响应优化的MATLAB工具

MATLAB提供了多种工具和函数，用于滤波器频率响应优化：

- **`fdesign` 函数：**用于设计各种类型的滤波器，并指定优化目标和约束。
- **`optimset` 函数：**用于设置优化算法的参数，例如最大迭代次数和容差。
- **`fminsearch` 函数：**用于执行梯度下降优化。
- **`ga` 函数：**用于执行遗传算法优化。
- **`pso` 函数：**用于执行粒子群优化。

通过结合这些工具，用户可以自动化滤波器频率响应优化过程，并快速找到满足特定应用需求的最佳滤波器参数。

# 5.1 信号噪声去除和增强

滤波器频率响应分析在信号处理中的一项重要应用是信号噪声去除和增强。噪声是信号中不期望的成分，它会干扰信号的分析和处理。滤波器可以用来去除噪声，同时保留信号的所需信息。

### 噪声去除

噪声去除的基本原理是利用滤波器将噪声成分从信号中分离出来。噪声通常具有特定的频率范围，而信号则具有不同的频率范围。通过设计一个滤波器，其通带覆盖信号的频率范围，而阻带覆盖噪声的频率范围，可以有效地去除噪声。

### 噪声增强

在某些情况下，需要增强信号中的特定频率成分，以突出信号的特征或改善其可读性。滤波器也可以用于此目的。通过设计一个滤波器，其通带覆盖要增强的频率范围，可以放大信号中的这些成分，从而增强信号的特征。

### 应用实例

滤波器频率响应分析在信号噪声去除和增强中的应用实例包括：

- **语音信号降噪：**去除语音信号中的背景噪声，如交通噪声或人群噪声，以提高语音清晰度。
- **图像降噪：**去除图像中的噪声，如椒盐噪声或高斯噪声，以增强图像质量。
- **医学信号增强：**增强医学信号中的特定频率成分，如心电图中的QRS波或脑电图中的阿尔法波，以改善诊断准确性。