MATLAB滤波器设计中的滤波器类型选择：针对不同需求选择最佳滤波器，提升信号处理效果

# 1. 滤波器基础**

滤波器是一种处理信号的装置，用于去除不需要的频率成分，增强所需的信息。在数字信号处理中，滤波器通过数学算法实现，称为数字滤波器。

数字滤波器根据其脉冲响应的无限或有限长度分为两类：无限脉冲响应 (IIR) 滤波器和有限脉冲响应 (FIR) 滤波器。IIR 滤波器具有无限长的脉冲响应，而 FIR 滤波器具有有限长的脉冲响应。

# 2. 滤波器类型的理论基础

### 2.1 数字滤波器的分类

数字滤波器根据其脉冲响应的长度可分为两大类：

- **无限冲激响应 (IIR) 滤波器：**脉冲响应无限长，即在输入信号消失后，滤波器输出仍会持续一段时间。
- **有限冲激响应 (FIR) 滤波器：**脉冲响应有限长，即在输入信号消失后，滤波器输出也会在有限时间内消失。

**2.1.1 IIR滤波器**

IIR滤波器使用反馈回路来实现滤波，其传递函数包含极点和零点。IIR滤波器具有以下特点：

- **低阶实现高阶滤波：**IIR滤波器可以用较低阶数实现高阶滤波，从而节省计算资源。
- **具有谐振：**IIR滤波器在谐振频率处具有较高的增益，可用于信号增强或谐振抑制。
- **稳定性问题：**IIR滤波器可能存在稳定性问题，需要仔细设计以避免振荡或不稳定。

**2.1.2 FIR滤波器**

FIR滤波器使用抽头延迟线来实现滤波，其传递函数仅包含零点。FIR滤波器具有以下特点：

- **线性相位：**FIR滤波器具有线性相位响应，不会引起信号失真。
- **稳定性：**FIR滤波器始终稳定，不会出现振荡或不稳定。
- **高阶实现低阶滤波：**FIR滤波器需要较高阶数才能实现低阶滤波，这可能会增加计算资源消耗。

### 2.2 滤波器响应的特性

滤波器的响应特性描述了其对输入信号的处理方式。主要特性包括：

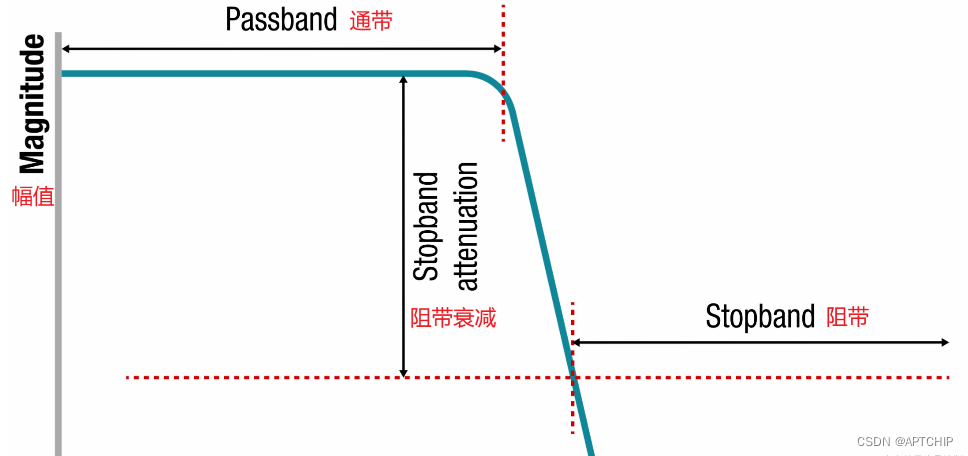
**2.2.1 通带和阻带**

- **通带：**滤波器允许通过的频率范围。
- **阻带：**滤波器衰减的频率范围。

**2.2.2 截止频率和通带增益**

- **截止频率：**通带和阻带之间的边界频率。
- **通带增益：**滤波器在通带内的增益，通常为 0 dB。

### 2.3 滤波器设计方法

滤波器设计方法可分为两类：

**2.3.1 频域设计**

频域设计方法直接在频率域中设计滤波器，通过指定通带、阻带、截止频率和通带增益等参数来生成滤波器系数。

**2.3.2 时域设计**

时域设计方法从滤波器的脉冲响应出发，通过优化时域性能来设计滤波器。时域设计方法通常用于设计 FIR 滤波器。

**代码示例：**

% 频域设计 IIR 低通滤波器
[b, a] = butter(6, 0.5);  % 6 阶，截止频率为 0.5

% 时域设计 FIR 低通滤波器
h = fir1(50, 0.5);  % 50 阶，截止频率为 0.5

**逻辑分析：**

`butter` 函数使用频域