奇异值分解（SVD）：降维、特征提取和图像处理的利器，掌握数据分析核心技术

# 1. 奇异值分解（SVD）概述**

奇异值分解（SVD）是一种强大的数学工具，用于分析矩阵并提取其关键特征。它在降维、特征提取和图像处理等领域有着广泛的应用。

SVD将一个矩阵分解成三个矩阵的乘积：一个左奇异向量矩阵、一个对角奇异值矩阵和一个右奇异向量矩阵。奇异值代表矩阵中方差最大的方向，奇异向量则代表这些方向。

通过SVD，我们可以对矩阵进行降维，提取其最重要的特征。此外，SVD在图像处理中也扮演着重要角色，它可以用于图像降噪、图像压缩和图像识别等任务。

# 2. SVD理论基础**

**2.1 线性代数基础**

奇异值分解（SVD）是线性代数中的一种重要技术，用于分析矩阵的结构和性质。为了理解SVD，首先需要了解一些线性代数的基础知识。

**矩阵：**矩阵是一个由数字排列成的矩形数组，表示一个线性变换。矩阵的维度由行数和列数决定，记作m×n。

**秩：**矩阵的秩表示矩阵中线性无关的行或列的最大数量。秩为r的矩阵称为r阶矩阵。

**正交矩阵：**正交矩阵是其转置等于其逆矩阵的方阵。正交矩阵保持向量的长度和之间的角度。

**2.2 奇异值和奇异向量**

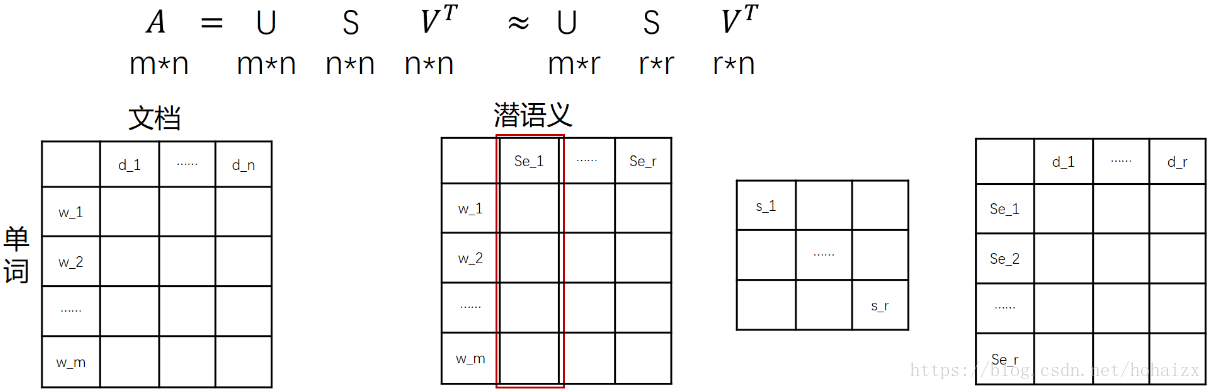
奇异值分解将一个m×n矩阵A分解成三个矩阵的乘积：

A = UΣV^T

其中：

* **U** 是一个m×m的正交矩阵，其列向量称为左奇异向量。
* **Σ** 是一个m×n的对角矩阵，其对角线上的元素称为奇异值。
* **V** 是一个n×n的正交矩阵，其列向量称为右奇异向量。

奇异值表示矩阵A中线性变换的强度。较大的奇异值对应于较强的变换，而较小的奇异值对应于较弱的变换。

奇异向量表示矩阵A中线性变换的方向。左奇异向量表示输入空间中的方向，而右奇异向量表示输出空间中的方向。

**2.3 SVD定理**

SVD定理指出，对于任何m×n矩阵A，都可以找到三个正交矩阵U、Σ和V，使得：

A = UΣV^T

其中Σ是一个对角矩阵，其对角线上的元素是非负实数，按降序排列。

SVD定理表明，任何矩阵都可以分解成三个正交矩阵的乘积，其中对角矩阵Σ表示矩阵的奇异值。

# 3. SVD实践应用

### 3.1 降维和特征提取

奇异值分解在降维和特征提取方面有着广泛的应用。它可以通过将高维数据投影到低维空间来减少数据维度，同时保留重要的信息。

#### 3.1.1 主成分分析（PCA）

主成分分析（PCA）是一种经典的降维技术，利用SVD来提取数据中的主成分。主成分是数据协方差矩阵的特征向量，它们表示数据方差最大的方向。

**PCA算法步骤：**

1. 对数据进行中心化，即减去均值。
2. 计算数据协方差矩阵。
3. 对协方差矩阵进行SVD分解，得到奇异值和奇异向量。
4. 选择前k个奇异值对应的奇异向量作为主成分。
5. 将数据投影到主成分空间，得到降维后的数据。

**代码示例：**

import numpy as np
from sklearn.decomposition import PCA

# 数据中心化
data = data - np.mean(data, axis=0)

# 计算协方差矩阵
cov_matrix = np.cov(data)

# SVD分解
U, s, Vh = np.linalg.svd(cov_matrix)

# 选择前k个主成分
k = 2
U_reduced = U[:, :k]

# 降维
data_reduced = np.dot(data, U_reduced)

**逻辑分析：**

* `U_reduced`包含了前k个主成分，它们是协方差矩阵的最大特征向量。
* `data_reduced`是数据在主成分空间的投影，维度为(n, k)，其中n为数据样本数。

#### 3.1.2 潜在语义分析（LSA）

潜在语义分析（LSA）是一种文本分析技术，利用SVD来提取文本中的潜在语义结构。它将文本表示为一个词项-文档矩阵，然后对矩阵进行SVD分解。

**LSA算法步骤：**

1. 构建词项-文档矩阵，其中行表示文档，列表示词项。
2. 对矩阵进行SVD分解，得到奇异值和奇异向量。
3. 选择前k个奇异值对应的奇异向量作为潜在语义因子。
4. 将词项和文档投影到潜在语义因子空间，得到语义表示。

**代码示例：**

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.decomposition import TruncatedSVD

# 构建词项-文档矩阵
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(documents)

# SVD分解
svd = TruncatedSVD(n_components=2)
U, s, Vh = svd.fit_transform(X)

# 词项和文档的语义表示
term_embeddings = U
doc_embeddings = Vh

**逻辑分析：**

* `term_embeddings`包含了词项的语义表示，维度为(m, k)，其中m为词项数。
* `doc_embeddings`包含了文档的语义表示，维度为(n, k)，其中n为文档数。

# 4. SVD进阶应用**

**4.1 推荐系统**

推荐系统旨在为用户推荐他们可能感兴趣的物品，例如电影、音乐或产品。SVD在推荐系统中发挥着至关重要的作用，因为它可以帮助从用户-物品交互数据中提取潜在特征。

**4.1.1 协同过滤**

协同过滤是一种推荐算法，它基于用户之间的相似性或物品之间的相似性。SVD可以用于计算用户和物品之间的相似性矩阵，该矩阵可以用来预测用户对特定物品的评分。

**4.1.2 矩阵分解**

矩阵分解是一种协同过滤技术，它将用户-物品交互矩阵分解为两个低秩矩阵。这些矩阵包含有关用户和物品的潜在特征，可用于进行推荐。

**代码块：**

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 用户-物品交互矩阵
user_item_matrix = np.array([[5, 4, 0],
                              [3, 2, 1],
                              [4, 3, 2]])

# 使用SVD分解矩阵
svd = TruncatedSVD(n_components=2)
svd.fit(user_item_matrix)

# 获取潜在特征矩阵
user_features = svd.components_
item_features = svd.components_.T

# 计算用户和物品之间的相似性
user_similarity = np.dot(user_features, user_features.T)
item_similarity = np.dot(item_features, item_features.T)

**逻辑分析：**

* `TruncatedSVD`类用于执行SVD，`n_components`参数指定要提取的潜在特征的数量。
* `fit()`方法将SVD拟合到用户-物品交互矩阵。
* `components_`属性包含潜在特征矩阵。
* `np.dot()`函数用于计算用户和物品之间的相似性。

**4.2 自然语言处理**

SVD在自然语言处理（NLP）中也有广泛的应用，因为它可以帮助从文本数据中提取有意义的特征。

**4.2.1 文本分类**

文本分类是一种NLP任务，涉及将文本文档分配到预定义的类别。SVD可以用于提取文本文档的潜在主题，这些主题可用于进行分类。

**4.2.2 机器翻译**

机器翻译是一种NLP任务，涉及将一种语言的文本翻译成另一种语言。SVD可以用于学习语言之间的潜在映射，从而提高翻译质量。

**代码块：**

import numpy as np
from sklearn.decomposition import LatentDirichletAllocation

# 文本语料库
corpus = ["This is a document about natural language processing.",
          "This is another document about machine learning.",
          "This is a document about data science."]

# 使用LDA提取潜在主题
lda = LatentDirichletAllocation(n_components=5)
lda.fit(corpus)

# 获取潜在主题
topics = lda.components_

**逻辑分析：**

* `LatentDirichletAllocation`类用于执行LDA，`n_components`参数指定要提取的潜在主题的数量。
* `fit()`方法将LDA拟合到文本语料库。
* `components_`属性包含潜在主题矩阵。

# 5. SVD在数据分析中的应用实例

SVD在数据分析领域有着广泛的应用，以下是一些具体的应用实例：

### 5.1 医疗诊断

在医疗领域，SVD可以用于从医疗图像中提取特征，辅助疾病诊断。例如，通过对CT或MRI图像进行SVD，可以提取出反映病变区域的奇异值和奇异向量，从而帮助医生更准确地识别和定位病灶。

### 5.2 金融预测

在金融领域，SVD可以用于分析金融数据，预测市场趋势。例如，通过对股票价格或经济指标进行SVD，可以提取出反映市场变化趋势的奇异值和奇异向量，从而帮助分析师预测未来的市场走势。

### 5.3 网络安全

在网络安全领域，SVD可以用于检测网络攻击和异常行为。例如，通过对网络流量数据进行SVD，可以提取出反映攻击或异常行为的奇异值和奇异向量，从而帮助安全分析师识别和应对潜在的威胁。

### 代码示例

以下是一个使用SVD进行医疗诊断的Python代码示例：

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 加载医疗图像数据
data = np.load('medical_images.npy')

# 应用SVD进行降维
svd = TruncatedSVD(n_components=2)
svd.fit(data)

# 获取奇异值和奇异向量
singular_values = svd.singular_values_
singular_vectors = svd.components_

# 使用奇异值和奇异向量提取特征
features = np.dot(data, singular_vectors)