SVD在行业中的趋势：新兴技术和应用领域，把握数据科学前沿

# 1. SVD简介**

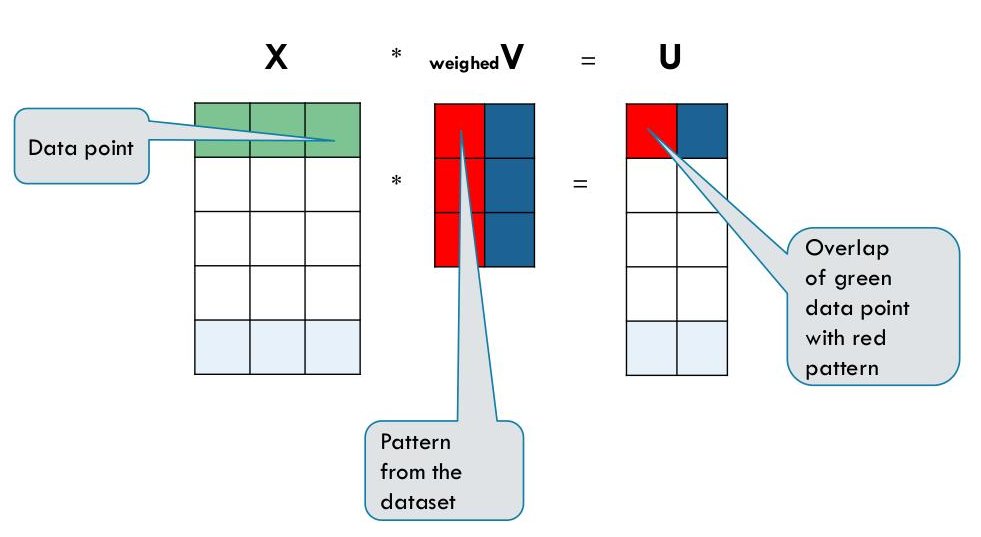
奇异值分解（SVD）是一种强大的数学技术，广泛应用于数据科学、机器学习和信号处理等领域。它将一个矩阵分解为三个矩阵的乘积：一个左奇异矩阵、一个对角奇异值矩阵和一个右奇异矩阵。

SVD揭示了矩阵的内在结构，允许我们提取有意义的信息。它提供了对矩阵秩、条件数和奇异空间的深入理解。通过分解矩阵，SVD可以帮助我们解决各种问题，包括降维、特征提取、推荐系统和图像处理。

# 2.1 奇异值分解的数学原理

奇异值分解（SVD）是一种强大的数学工具，用于将矩阵分解为一系列奇异值和奇异向量的乘积。其数学原理如下：

**定义：**

对于一个实数矩阵 **A** ∈ R^(m×n)，其奇异值分解为：

A = UΣV^T

其中：

* **U** ∈ R^(m×m) 是左奇异向量矩阵，其列向量是 **A** 的左奇异向量。
* **Σ** ∈ R^(m×n) 是奇异值矩阵，其对角线元素是 **A** 的奇异值，按降序排列。
* **V** ∈ R^(n×n) 是右奇异向量矩阵，其列向量是 **A** 的右奇异向量。

**奇异值：**

奇异值是 **Σ** 对角线上的非负实数。它们表示 **A** 的秩和线性独立的列和行向量的数量。

**奇异向量：**

奇异向量是 **U** 和 **V** 的列向量。左奇异向量是 **A** 的行向量的线性组合，而右奇异向量是 **A** 的列向量的线性组合。

**分解过程：**

SVD 可以通过以下步骤计算：

1. 计算 **A** 的协方差矩阵 **C = A^TA**。
2. 计算 **C** 的特征值和特征向量。
3. **U** 的列向量是 **C** 的特征向量，**Σ** 的对角线元素是 **C** 的特征值的平方根，**V** 的列向量是 **A** 的右奇异向量。

**参数说明：**

* **A：** 输入矩阵
* **U：** 左奇异向量矩阵
* **Σ：** 奇异值矩阵
* **V：** 右奇异向量矩阵

**代码块：**

import numpy as np

def svd(A):
    """
    计算矩阵的奇异值分解

    参数：
        A：输入矩阵

    返回：
        U：左奇异向量矩阵
        Σ：奇异值矩阵
        V：右奇异向量矩阵
    """

    C = np.dot(A.T, A)
    eigenvalues, eigenvectors = np.linalg.eig(C)
    U = eigenvectors
    Σ = np.sqrt(eigenvalues)
    V = np.dot(A, U) / Σ

    return U, Σ, V

**逻辑分析：**

* 该代码首先计算协方差矩阵 **C**。
* 然后计算 **C** 的特征值和特征向量。
* 最后，根据特征值和特征向量计算 **U**、**Σ** 和 **V**。

# 3. SVD在数据科学中的应用

### 3.1 降维和特征提取

奇异值分解（SVD）在数据科学中的一项重要应用是降维和特征提取。降维是指将高维数据投影到低维空间，而特征提取是指从数据中识别出有意义的模式和特征。

SVD可用于降维，因为它可以将数据分解成奇异值、左奇异向量和右奇异向量的集合。奇异值表示数据的方差，而奇异向量表示数据的协方差。通过选择具有最大奇异值的前几个奇异向量，我们可以将数据投影到低维空间，同时保留大部分信息。

import numpy as np
from sklearn.decomposition import TruncatedSVD

# 创建一个高维数据矩阵
X = np.random.randn(100, 1000)

# 使用SVD进行降维
svd = TruncatedSVD(n_components=100)
X_reduced = svd.fit_transform(X)

# 打印降维后的数据
print(X_reduced.shape)

### 3.2 推荐系统

SVD在推荐系统中也扮演着重要角色。推荐系统旨在根据用户的过去行为预测用户可能感兴趣的物品。SVD可以用于构建用户-物品协同过滤矩阵，其中每个元素表示用户对特定物品的评分。

通过对协同过滤矩阵进行SVD，我们可以将用户和物品分解成低维特征空间。这些特征可以用来预测用户对未评分物品的评分，从而生成个性化的推荐。

import pandas as pd
from sklearn.metrics.pairwise import cosine_similarity

# 创建一个用户-物品评分矩阵
ratings = pd.DataFrame({
    'user_id': [1, 1, 2, 2, 3],
    'item_id': ['A', 'B', 'C', 'D', 'E'],
    'rating': [5, 4, 3, 2, 1]
})

# 使用SVD构建协同过滤矩阵
user_item_matrix = ratings.pivot_table(index='user_id', columns='item_id', values='r