深入探讨IIR滤波器在信号处理中的作用：揭示滤波器在信号处理中的价值

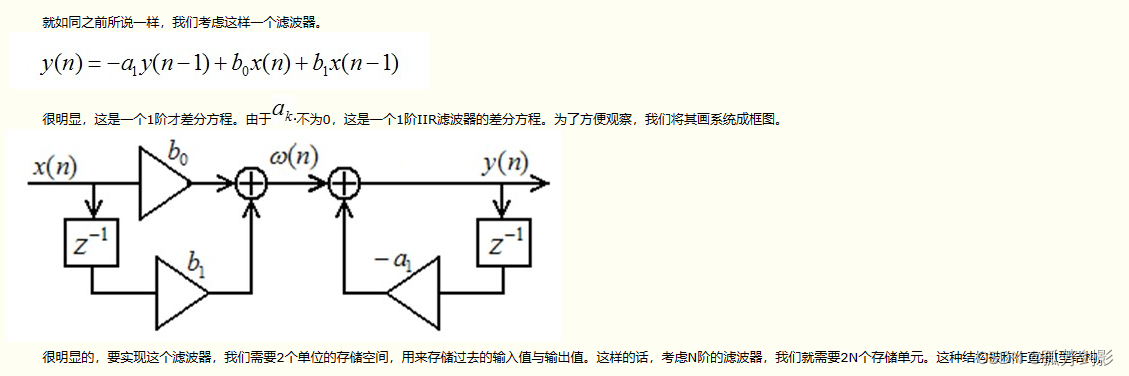
# 1. IIR滤波器的理论基础

IIR（无限脉冲响应）滤波器是一种线性时不变滤波器，其输出不仅与当前输入有关，还与过去输入有关。IIR滤波器具有以下特点：

- **无限脉冲响应：**IIR滤波器的输出对输入信号的响应持续无限长，即使输入信号已停止。
- **反馈：**IIR滤波器使用反馈回路，将输出信号的一部分反馈到输入端，从而实现滤波效果。
- **稳定性：**IIR滤波器必须保持稳定，即输出信号不会随时间发散或振荡。

# 2. IIR滤波器设计与实现

### 2.1 IIR滤波器的设计方法

#### 2.1.1 双线性变换法

双线性变换法是一种将模拟滤波器设计方法应用于数字滤波器设计的方法。其基本思想是将模拟滤波器的传递函数s域变换到z域，从而得到数字滤波器的传递函数。

**步骤：**

1. 将模拟滤波器的传递函数H(s)写成s域多项式的形式：H(s) = N(s)/D(s)
2. 用双线性变换公式将s替换为z：s = 2(z - 1)/(z + 1)
3. 将变换后的传递函数H(z)写成z域多项式的形式：H(z) = N(z)/D(z)

**代码块：**

import numpy as np

def bilinear_transform(H_s, fs):
    """
    双线性变换法设计IIR滤波器

    参数：
        H_s: 模拟滤波器的传递函数
        fs: 采样频率

    返回：
        H_z: 数字滤波器的传递函数
    """

    # 将s域传递函数转换为多项式形式
    N_s, D_s = H_s.num, H_s.den

    # 进行双线性变换
    z = np.exp(1j * 2 * np.pi * fs)
    s = 2 * (z - 1) / (z + 1)

    # 将变换后的传递函数转换为z域多项式形式
    N_z = np.polyval(N_s, s)
    D_z = np.polyval(D_s, s)

    H_z = N_z / D_z

    return H_z

**逻辑分析：**

该代码实现了双线性变换法。它首先将模拟滤波器的传递函数转换为多项式形式。然后，它应用双线性变换公式将s替换为z。最后，它将变换后的传递函数转换为z域多项式形式。

#### 2.1.2 脉冲响应不变法

脉冲响应不变法是一种通过匹配模拟滤波器的脉冲响应来设计数字滤波器的方法。其基本思想是将模拟滤波器的脉冲响应离散化，并作为数字滤波器的系数。

**步骤：**

1. 获取模拟滤波器的脉冲响应h(t)
2. 对h(t)进行离散化，得到数字滤波器的系数h[n]
3. 将h[n]作为数字滤波器的传递函数的系数

**代码块：**

import numpy as np

def impulse_invariant_method(h_t, fs):
    """
    脉冲响应不变法设计IIR滤波器

    参数：
        h_t: 模拟滤波器的脉冲响应
        fs: 采样频率

    返回：
        H_z: 数字滤波器的传递函数
    """

    # 对脉冲响应进行离散化
    h_n = np.array([h_t(n / fs) for n in range(len(h_t))])

    # 将离散化的脉冲响应作为传递函数的系数
    H_z = np.poly1d(h_n)

    return H_z

**逻辑分析：**

该代码实现了脉冲响应不变法。它首先对模拟滤波器的脉冲响应进行离散化。然后，它将离散化的脉冲响应作为数字滤波器的传递函数的系数。

### 2.2 IIR滤波器的实现

#### 2.2.1 直接形式

直接形式是实现IIR滤波器最直接的方法。其基本思想是将滤波器的传递函数直接转换为差分方程，然后使用差分方程来更新滤波器的状态。

**代码块：**

import numpy as np

class DirectFormIIRFilter:
    def __init__(self, b, a):
        """
        直接形式IIR滤波器

        参数：
            b: 分子多项式的系数
            a: 分母多项式的系数
        """

        self.b = b
        self.a = a
        self.x = np.zeros(len(a) - 1)
        self.y = np.zeros(len(b) - 1)

    def filter(self, x):
        """
        滤波函数

        参数：
            x: 输入信号

        返回：
            y: 输出信号
        """

        # 更新状态
        self.x = np.roll(self.x, -1)
        self.x[0] = x

        # 计算输出
        y = np.dot(self.b, self.x) - np.dot(self.a[1:], self.y)
        self.y = np.roll(self.y, -1)
        self.y[0] = y

        return y

**逻辑分析：**

该代码实现了直接形式IIR滤波器。它首先初始化滤波器的状态，包括输入信号的过去值x和输出信号的过去值y。然后，它更新状态并计算输出。

#### 2.2.2 级联形式

级联形式将IIR滤波器分解为多个一阶或二阶滤波器，然后将这些滤波器级联起来。这种形式可以降低滤波器的复杂度和实现难度。

**代码块：**

import numpy as np

class CascadeFormIIRFilter:
    def __init__(self, b, a):
        """
        级联形式IIR滤波器

        参数：
            b: 分子多项式的系数
            a: 分母多项式的系数
        """

        self.filters = []
        for i in range(len(b)):
            self.filters.append(DirectFormIIRFilter(b[i], a))

    def filter(self, x):