【模型评估指标】衡量机器学习性能的黄金标准：专家教你如何评价


参考资源链接：[《机器学习(周志华)》学习笔记.pdf](https://wenku.csdn.net/doc/6412b753be7fbd1778d49e56?spm=1055.2635.3001.10343)
# 1. 机器学习模型评估的重要性

在机器学习领域，模型的评估是检验算法有效性、可靠性的关键步骤。它不仅关系到模型在数据集上的表现，更是决定模型能否在现实世界中发挥预期作用的重要依据。对模型评估的重视程度，直接体现了数据科学家对模型质量的追求。本章将探讨为什么模型评估如此重要，并将为后续章节的深入分析打下基础。

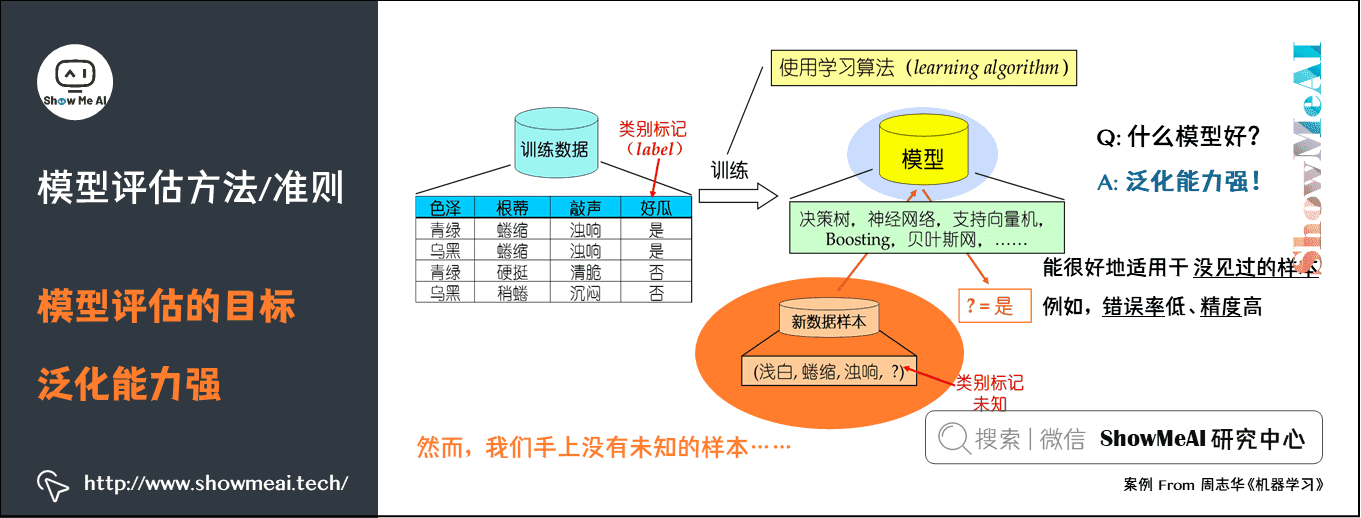
随着机器学习的应用变得越来越普遍，准确预测未知数据的能力变得至关重要。评估模型可以揭示模型的强项和弱点，帮助研究人员理解其潜在的偏差，并为优化模型提供方向。良好的评估机制可以提升模型的泛化能力，使其在未见数据上的表现更加稳定可靠。接下来的章节将详细介绍不同类型的机器学习模型评估方法，以及如何在实际项目中应用这些知识。

# 2. 分类模型的性能评估

### 2.1 准确度与精确度

#### 2.1.1 准确度的定义与计算
准确度（Accuracy）是分类模型性能评估中最基本的指标，它表示模型正确预测的样本数量占总样本数量的比例。准确度的计算公式为：

accuracy = (TP + TN) / (TP + TN + FP + FN)

其中，TP（True Positive）代表真正类的样本数，TN（True Negative）代表真负类的样本数，FP（False Positive）代表假正类的样本数，FN（False Negative）代表假负类的样本数。

在使用准确度时，需注意其可能带来的误导。当数据集极度不平衡时，例如在正负样本比例为1:1000的情况下，即使模型总是预测为负类，准确度也可能高达99.9%。在这种情况下，准确度并不能真实反映模型的预测能力。

#### 2.1.2 精确度的定义与计算
精确度（Precision）是指在模型预测为正类的结果中，有多少比例是真的正类。精确度的计算公式为：

precision = TP / (TP + FP)

精确度关注的是模型预测结果的质量，尤其适用于对正类预测的准确性有较高要求的场景。例如，在医疗诊断中，我们更关心的是模型预测疾病患者的准确率，因为一个假阳性的结果可能会引起不必要的恐慌或治疗。

### 2.2 召回率与F1分数

#### 2.2.1 召回率的含义和应用场景
召回率（Recall），又称为真正类率（True Positive Rate, TPR），它衡量了所有实际正类中被模型正确识别为正类的比例。召回率的计算公式为：

recall = TP / (TP + FN)

召回率在某些情况下更受关注，例如在垃圾邮件检测中，我们更关心的是尽可能多地检出垃圾邮件（FN要尽可能小），以免用户错过重要邮件。

#### 2.2.2 F1分数的计算及其重要性
F1分数是准确度和召回率的调和平均，它的目的是找到一个平衡点，特别是当两者难以兼得时。F1分数的计算公式为：

F1 = 2 * (precision * recall) / (precision + recall)

F1分数给出了一个单一的分数，使得比较不同模型时更公正。对于那些需要平衡精确度和召回率的二分类问题，F1分数是一个更好的评估指标。

### 2.3 ROC曲线与AUC值

#### 2.3.1 ROC曲线的工作原理
ROC曲线（Receiver Operating Characteristic Curve）是一种重要的分类性能评估工具。它通过绘制不同分类阈值下的真正类率（召回率）和假正类率（False Positive Rate, FPR）来展现模型的表现。ROC曲线越靠近左上角，表示模型性能越好。

from sklearn.metrics import roc_curve
import matplotlib.pyplot as plt

fpr, tpr, thresholds = roc_curve(y_true, y_scores)
plt.plot(fpr, tpr)
plt.xlabel('FPR')
plt.ylabel('TPR')
plt.title('ROC Curve')
plt.show()

在上述代码中，`y_true`是真实的标签，`y_scores`是模型预测的分数。

#### 2.3.2 AUC值的意义和解读
AUC（Area Under the Curve）值是ROC曲线下面积的度量。AUC值的范围在0到1之间，值越接近1，表示模型的分类效果越好。AUC值提供了一个单一的数值来评估模型的整体性能，不受数据不平衡的影响。

from sklearn.metrics import roc_auc_score

auc_score = roc_auc_score(y_true, y_scores)
print("The AUC score is:", auc_score)

在实际应用中，如果AUC值接近0.5，那么模型几乎没有预测能力；如果接近1，则表示模型具有很强的预测能力。AUC是评估分类模型的有力工具，特别是在数据不平衡的情况下。

# 3. 回归模型的评估方法

回归分析是机器学习中广泛使用的一种统计技术，用于建立变量之间的关系模型。在评估回归模型时，我们通常关注模型对数据的拟合程度以及预测的准确性。本章将深入探讨几种常用的回归模型评估指标：均方误差与均方根误差、决定系数R²和平均绝对误差，并解释它们在实际应用中的意义。

## 3.1 均方误差与均方根误差

### 3.1.1 均方误差的计算和优缺点

均方误差（Mean Squared Error, MSE）是一种常用的回归模型评估指标。它通过计算实际观测值与模型预测值差值的平方和，来衡量模型预测的准确性。MSE能够强调较大的预测误差，因此对于异常值比较敏感。

计算公式为：
\[ MSE = \frac{1}{N}\sum_{i=1}^{N} (y_i - \hat{y_i})^2 \]
其中，\(y_i\) 是第 \(i\) 个样本的实际值，\(\hat{y_i}\) 是模型预测的值，\(N\) 是样本数量。

**优点：**
- 明确表示预测值与实际值之间的差异。
- 由于平方的影响，对异常值更加敏感，这有助于我们识别模型在极端值上的表现。

**缺点：**
- 对于异常值过于敏感，可能会导致模型整体评估失衡。
- 无法直接反映预测值相对于实际值的大小关系，因为误差是平方的。

### 3.1.2 均方根误差的特点和应用场景

均方根误差（Root Mean Squared Error, RMSE）是MSE的平方根，它将MSE转换回原始数据的单位，因此更容易解释和比较。

计算公式为：
\[ RMSE = \sqrt{\frac{1}{N}\sum_{i=1}^{N} (y_i - \hat{y_i})^2} \]

**特点：**
- 与MSE相比，RMSE的量纲与原始数据相同，便于解释。
- 同样保持了对异常值的敏感性。

**应用场景：**
- RMSE常用于评估预测模型，特别是在金融领域，因其结果更符合实际的预测误差。
-