【全加器设计秘籍】：从零开始到高级仿真实战


# 摘要
全加器作为一种基本的数字逻辑电路组件，在集成电路设计中扮演着重要的角色。本文首先介绍了全加器的数字逻辑基础和理论设计，包括其定义、功能、数学模型和真值表。随后，本文探讨了全加器的逻辑门实现和理论分析，着重分析了逻辑电路的时序特性以及设计错误的检测与校正方法。硬件实现与仿真章节详细说明了全加器的物理搭建和调试，同时介绍了仿真工具的选择与应用。此外，本文还探讨了全加器在复杂电路中的高级应用以及优化技巧，并讨论了能耗和面积优化的可能性。最后，文章展望了全加器技术的未来发展趋势，包括新型材料的应用、集成电路小型化的影响以及全加器在新兴计算领域中的应用潜力。

# 关键字
全加器；数字逻辑；逻辑门实现；时序分析；硬件搭建；仿真测试；优化技巧；故障诊断；新型材料；集成电路小型化

参考资源链接：[Multisim数电仿真实验：半加器与全加器逻辑功能分析](https://wenku.csdn.net/doc/6401ac10cce7214c316ea802?spm=1055.2635.3001.10343)
# 1. 全加器的数字逻辑基础

## 1.1 数字逻辑概述

数字逻辑是计算机科学和电子工程中不可或缺的一部分，它涉及到使用抽象的符号（通常是0和1）来表示信息，并通过逻辑运算来处理这些信息。数字逻辑电路的构建基础是逻辑门，它们可以执行如与（AND）、或（OR）、非（NOT）等基本操作。这些逻辑门以特定的方式组合起来，可以构造出更复杂的电路，例如全加器。

## 1.2 全加器的重要性

全加器是数字电路中最基本的算术构建单元之一，它的功能是实现三个一位二进制数的加法运算。这三位二进制数分别是两个加数位和一个进位输入位，全加器会输出一个和位和一个进位输出位。全加器在数字系统中的应用非常广泛，不仅限于基本的算术运算，还扩展到数据加密、解密以及各种数字信号处理等领域。

## 1.3 全加器的数字逻辑应用

在数字逻辑设计中，全加器能够实现更复杂的算术操作的基础。例如，多个全加器可以串联形成多位二进制加法器，进一步可以构建减法器、乘法器等更复杂的算术单元。全加器的设计不仅关系到数字电路的速度和面积效率，同时也影响着整个系统的性能和可靠性。

# 2. 全加器的理论设计与分析

### 2.1 数字电路中的全加器概念

#### 2.1.1 全加器的定义和功能

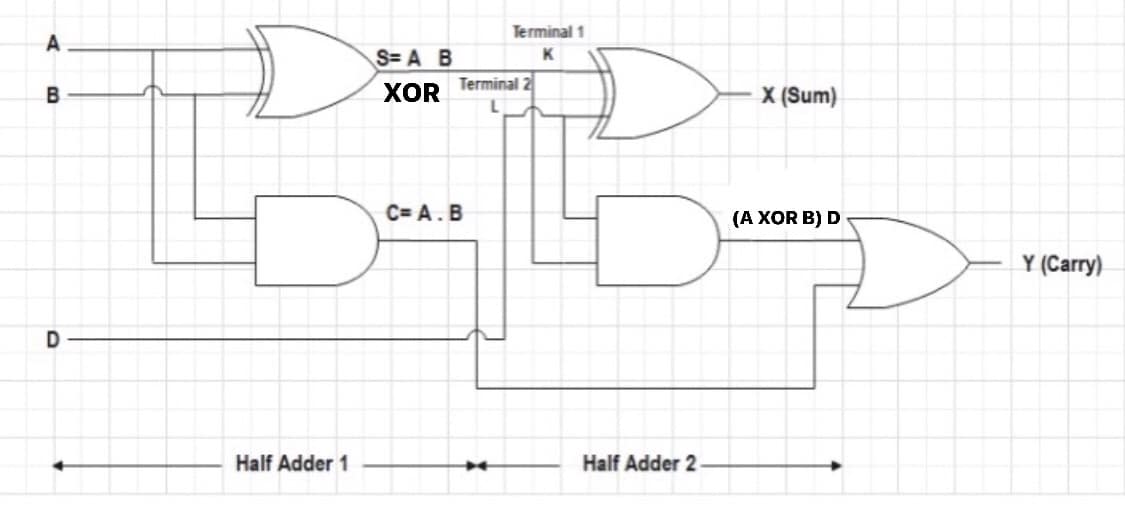
全加器（Full Adder）是数字电路中执行加法操作的基本组件之一。它能够处理三个位的输入：两个加数位（记为A和B）和一个进位输入位（记为Cin），产生两个输出：和位（记为Sum）和进位输出位（记为Cout）。全加器不仅计算两个输入位的和，还考虑了进位输入，能够实现从一个位到下一个位的进位传递。

#### 2.1.2 全加器的数学模型和真值表

全加器的数学模型可以通过逻辑表达式来描述其功能：

Sum = A ⊕ B ⊕ Cin
Cout = (A ∧ B) ∨ (Cin ∧ (A ⊕ B))

其中，⊕表示异或（XOR）操作，∧表示与（AND）操作，∨表示或（OR）操作。这是全加器最基础的布尔代数表达式。

为了更直观理解全加器的工作原理，我们可以列出一个全加器的真值表：
| A | B | Cin | Sum | Cout |
|---|---|-----|-----|------|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

通过真值表，我们可以观察到，当输入A、B以及进位Cin任一为1时，和位Sum可能会改变；而只有当A和B同时为1时，或者其中一为1且Cin为1时，Cout才可能为1。

### 2.2 全加器的逻辑门实现

#### 2.2.1 基本逻辑门与全加器的连接

全加器的逻辑门实现涉及到基本的数字逻辑门：AND门、OR门和XOR门。每个全加器的输出都可以用这些基本逻辑门的组合来实现。以下是全加器逻辑门实现的示意图：

graph TD
    A[输入A] -->|异或| XOR1[Sum]
    B[输入B] -->|异或| XOR2[Sum]
    Cin[进位输入] -->|与| AND1[A AND B]
    AND1 -->|或| OR1[Cout]
    A -->|与| AND2[A AND Cin]
    B -->|与| AND3[B AND Cin]
    AND2 -->|或| OR1[Cout]
    AND3 -->|或| OR1[Cout]
    XOR1 -->|异或| AND4[Sum AND Cin]
    AND4 -->|或| OR1[Cout]

#### 2.2.2 优化逻辑门配置的方法

逻辑门配置优化是减少电路复杂度和降低成本的关键。一种常见的优化方法是通过简化布尔表达式来减少所需的逻辑门数量。例如，在全加器设计中，可以利用代数简化技术减少组合逻辑门的数量：

flowchart LR
    A[输入A] -->|异或| XOR1[Sum]
    B[输入B] -->|异或| XOR2[Sum]
    Cin[进位输入] -->|与| AND1[A AND B]
    A -->|与| AND2[A AND Cin]
    B -->|与| AND3[B AND Cin]
    AND1 -->|或| OR1[Cout]
    AND2 -->|或| OR1[Cout]
    AND3 -->|或| OR1[Cout]

### 2.3 全加器的理论分析

#### 2.3.1 逻辑电路的时序分析

全加器的时序分析关注的是电路的响应时间以及输入信号变化对输出信号的影响。在设计中，我们需要确保每个阶段的逻辑门延迟是匹配的，以避免数据在时钟周期内