【数字电路设计高级技巧】：半加器和全加器的仿真艺术


# 摘要
本文全面介绍了数字电路设计的基础知识，重点讨论了半加器和全加器的理论基础、设计原理及其在复杂电路中的应用。通过分析二进制加法原理，文章阐述了半加器和全加器的工作机制，包括逻辑表达式、真值表和电路实现。进一步地，本文提供了半加器和全加器在仿真工具中的实践应用，并探讨了仿真过程中的常见问题及其解决方法。最后，文章探讨了高级仿真技巧和性能优化策略，并展示了半加器和全加器在创新设计及教育研究领域的应用实例，为数字电路设计者提供了一系列实用的工具和方法。

# 关键字
数字电路设计；半加器；全加器；仿真工具；性能优化；创新应用

参考资源链接：[Multisim数电仿真实验：半加器与全加器逻辑功能分析](https://wenku.csdn.net/doc/6401ac10cce7214c316ea802?spm=1055.2635.3001.10343)
# 1. 数字电路设计概述

数字电路设计是构建现代电子设备不可或缺的一部分。从简单的逻辑门到复杂的微处理器，数字电路都扮演着核心角色。为了设计出高效、可靠的数字电路，我们需要了解其基本组成、工作原理以及设计流程。本章将带领读者入门数字电路设计的世界，概述这一领域的核心概念和基础理论。我们将讨论数字信号与模拟信号的区别，数字电路设计的基本步骤，以及在设计过程中常见的挑战和解决方案。通过理论学习和实例分析，本章为理解后续章节内容打下坚实的基础。

# 2. 半加器和全加器的理论基础

在数字逻辑设计领域，加法器是最基础且重要的组件之一。在本章节中，我们将深入探讨半加器和全加器的工作原理和设计过程，这些是实现数字电路加法操作的关键元件。在详细讲解之前，需要强调的是，只有完全理解了加法器的理论基础，我们才能正确地设计和实现它们。

## 2.1 二进制加法原理

### 2.1.1 二进制数系统的加法规则

二进制加法是现代数字电路设计的核心。它基于简单的规则：0+0=0，0+1=1+0=1，1+1=10。这些规则是所有二进制算术运算的基石。二进制系统中，最高位的进位称为进位（Carry），而结果部分称为和（Sum）。在二进制加法中，进位只可能发生在1+1的情况下，并且当两个二进制位相加产生进位时，进位结果将在下一位的计算中加入。

### 2.1.2 进位与和的概念

在二进制加法中，进位和和是两个核心概念。"和"是当前位加法的结果，而"进位"是在位加法中产生且需要传递到更高一位的结果。了解和掌握这两个概念对于设计和优化加法器至关重要。

## 2.2 半加器的设计与工作原理

### 2.2.1 半加器的逻辑表达式与真值表

半加器（Half Adder）是一种简单的组合逻辑电路，它可以实现两个一位二进制数的加法运算。半加器有两个输入：A和B，以及两个输出：和（S）和进位（C）。半加器的逻辑表达式可以描述如下：

- 和 S = A XOR B
- 进位 C = A AND B

真值表为：

| A | B | S（和）| C（进位）|
|---|---|--------|----------|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |

### 2.2.2 半加器的电路实现

半加器可以通过基本的逻辑门实现。在硬件实现中，通常使用异或门（XOR）来生成和（S），使用与门（AND）来生成进位（C）。例如，对于半加器的实现，我们可以使用以下的Verilog代码：

module half_adder(
    input wire A,
    input wire B,
    output wire Sum,
    output wire Carry
);
    assign Sum = A ^ B; // 异或门实现和
    assign Carry = A & B; // 与门实现进位
endmodule

在上述代码中，`assign`语句用于为输出信号赋值。`A ^ B`计算A和B的异或结果，对应和（Sum）输出；`A & B`计算A和B的与结果，对应进位（Carry）输出。这个简单的模块能够描述半加器的行为。

## 2.3 全加器的设计与工作原理

### 2.3.1 全加器的逻辑表达式与真值表

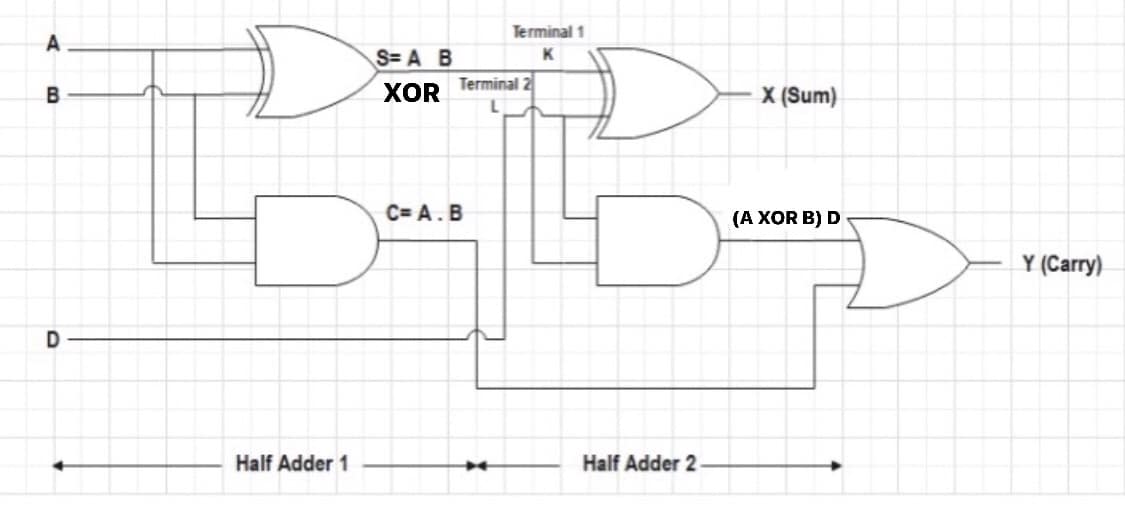
全加器（Full Adder）是半加器的扩展，能够处理三个一位二进制数的加法，包括两个输入位和一个来自低位的进位输入。全加器有三个输入：A、B和进位输入（Cin），以及两个输出：和（S）和进位输出（Cout）。全加器的逻辑表达式可以描述如下：

- 和 S = A XOR B XOR Cin
- 进位输出 Cout = (A AND B) OR (B AND Cin) OR (A AND Cin)

真值表为：

| A | B | Cin | S（和）| Cout（进位输出）|
|---|---|-----|--------|-----------------|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |

### 2.3.2 全加器的电路实现

全加器比半加器复杂，因为它涉及更多的逻辑门。在实现全加器时，我们可以使用逻辑门（比如AND、OR和XOR门）组合来构建。下面展示了如何用Verilog代码描述全加器：

module full_adder(
    input wire A,
    input wire B,
    input wire Cin,
    output wire