正弦波在数学中的应用：三角函数、微积分，领略数学之美，提升数学素养

# 1. 正弦波的数学基础

正弦波是一种周期性的数学函数，广泛应用于科学、工程和技术领域。它由以下公式定义：

y = A * sin(ωt + φ)

其中：

* A 是正弦波的振幅，表示波峰和波谷之间的距离。
* ω 是正弦波的角频率，表示波的周期性，单位为弧度/秒。
* t 是时间变量，表示正弦波在时间轴上的位置。
* φ 是正弦波的相位角，表示波在时间轴上的偏移量。

# 2. 正弦波在三角函数中的应用

### 2.1 三角函数的定义和性质

**2.1.1 三角函数的定义域和值域**

三角函数定义在实数域上，其值域因函数而异。

| 三角函数 | 定义域 | 值域 |
|---|---|---|
| 正弦函数 (sin) | (-∞, ∞) | [-1, 1] |
| 余弦函数 (cos) | (-∞, ∞) | [-1, 1] |
| 正切函数 (tan) | (-π/2, π/2) | (-∞, ∞) |

**2.1.2 三角函数的周期性**

三角函数具有周期性，其周期为 2π。这意味着对于任意实数 x 和正整数 n，有：

sin(x + 2πn) = sin(x)
cos(x + 2πn) = cos(x)
tan(x + πn) = tan(x)

### 2.2 正弦波在三角函数中的表示

**2.2.1 正弦函数的图像和性质**

正弦函数的图像是一个周期性的波形，其振幅为 1，周期为 2π。正弦函数的图像具有以下性质：

- 在区间 [0, π] 上单调递增
- 在区间 [π, 2π] 上单调递减
- 在 x = 0 和 x = π 时取极值 1
- 在 x = π/2 和 x = 3π/2 时取极值 -1

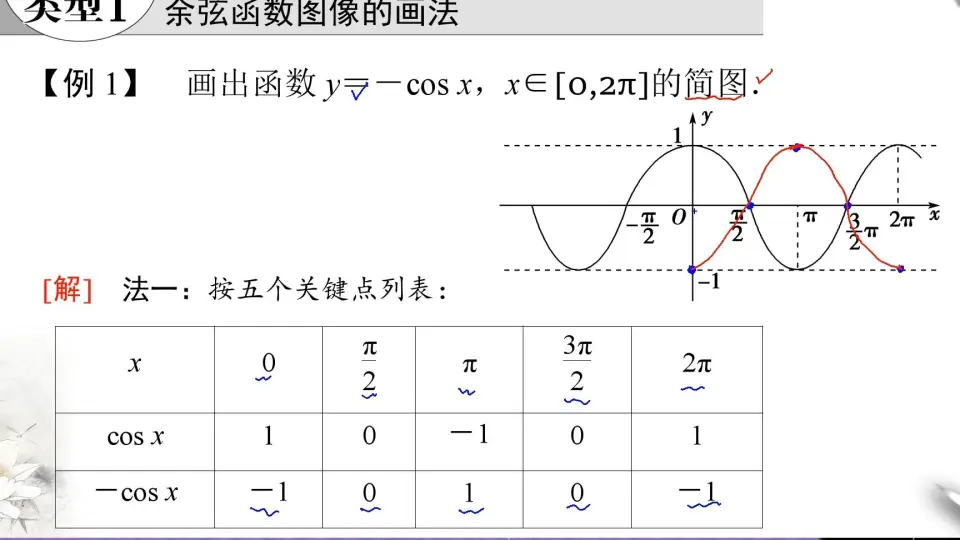
**2.2.2 余弦函数和正切函数的图像和性质**

余弦函数和正切函数的图像也是周期性的波形，但其振幅和周期与正弦函数不同。

| 三角函数 | 图像 | 振幅 | 周期 |
|---|---|---|---|
| 余弦函数 (cos) | 正弦函数的平移 | 1 | 2π |
| 正切函数 (tan) | 正弦函数和余弦函数的比值 | 无穷大 | π |

**代码块：绘制正弦函数、余弦函数和正切函数的图像**

import matplotlib.pyplot as plt

# 定义 x 轴范围
x = np.linspace(-2*np.pi, 2*np.pi, 100)

# 计算正弦函数、余弦函数和正切函数的值
y_sin = np.sin(x)
y_cos = np.cos