傅里叶变换与正弦波：从时域到频域，解锁信号的隐藏信息

# 1. 傅里叶变换的理论基础

傅里叶变换是一种数学变换，它将一个时域信号（或函数）转换为一个频域表示。通过傅里叶变换，我们可以分析信号的频率成分，从而深入了解其特性。

傅里叶变换的数学定义如下：

F(ω) = ∫_{-\∞}^{\∞} f(t)e^(-iωt) dt

其中：

* `F(ω)` 是频域表示
* `f(t)` 是时域信号
* `ω` 是角频率

傅里叶变换的逆变换为：

f(t) = (1/2π) ∫_{-\∞}^{\∞} F(ω)e^(iωt) dω

# 2. 傅里叶变换的实用应用

傅里叶变换在信号分析、图像处理和数据压缩等领域有着广泛的应用。本章将探讨傅里叶变换在这些领域的具体应用，并深入分析其背后的原理和技术。

### 2.1 信号分析与处理

#### 2.1.1 频谱分析

频谱分析是傅里叶变换在信号分析中的重要应用之一。它通过将时域信号分解为频率分量，揭示信号的频率特性。频谱分析广泛用于以下领域：

- **声音分析：**识别和分析声音中的不同音调和泛音。
- **振动分析：**检测机器或结构中的振动模式和频率。
- **雷达和声纳：**识别和跟踪目标的频率特征。

#### 2.1.2 滤波与降噪

傅里叶变换还可以用于滤波和降噪。通过在频域中选择性地移除或增强特定频率分量，可以实现以下目的：

- **低通滤波：**去除高频噪声，保留低频分量。
- **高通滤波：**去除低频分量，保留高频分量。
- **带通滤波：**只保留特定频率范围内的分量。
- **带阻滤波：**去除特定频率范围内的分量。

### 2.2 图像处理

#### 2.2.1 图像增强

傅里叶变换在图像增强中扮演着至关重要的角色。通过在频域中对图像进行操作，可以实现以下增强效果：

- **锐化：**增强图像边缘和细节。
- **平滑：**去除图像中的噪声和瑕疵。
- **对比度调整：**增强图像的对比度和亮度。
- **色彩校正：**调整图像的色彩平衡和饱和度。

#### 2.2.2 图像分割

图像分割是将图像分解为不同区域或对象的过程。傅里叶变换可以用于分割图像中的对象，原理如下：

- **频域分割：**在频域中，不同对象通常占据不同的频率范围。通过选择性地提取特定频率分量，可以分割出不同的对象。
- **纹理分割：**傅里叶变换可以提取图像的纹理特征。通过分析纹理差异，可以分割出具有不同纹理的区域。

### 2.3 数据压缩

#### 2.3.1 音频压缩

音频压缩是将音频信号转换为更小文件大小的过程。傅里叶变换在音频压缩中发挥着重要作用：

- **感知编码：**傅里叶变换可以将音频信号分解为频率分量。通过去除人耳不敏感的高频分量，可以实现音频压缩。
- **子带编码：**傅里叶变换可以将音频信号分解为不同频率子带。通过对每个子带进行单独编码，可以优化压缩效率。

#### 2.3.2 图像压缩

图像压缩是将图像转换为更小文件大小的过程。傅里叶变换在图像压缩中也有广泛的应用：

- **JPEG 压缩：**JPEG 压缩使用傅里叶变换将图像分解为频率分量。通过对高频分量进行量化和编码，可以实现图像压缩。
- **PNG 压缩：**PNG 压缩使用傅里叶变换将图像分解为无损的频率分量。通过对频率分量进行无损编码，可以实现图像压缩。

# 3.1 正弦波的性质和应用

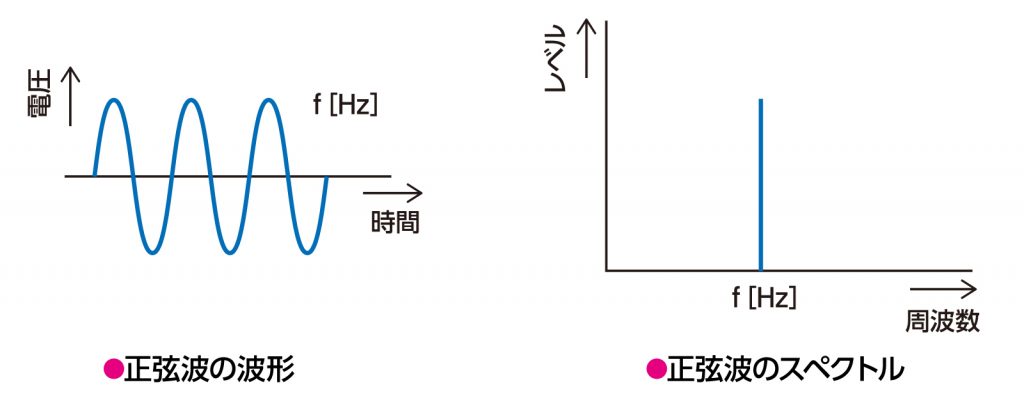
#### 3.1.1 正弦波的方程和图形

正弦波是一种周期性的函数，其方程为：

y = A * sin(2πft + φ)

其中：

* A：波幅，表示波的振幅
* f：频率，表示波在单位时间内的重复次数
* t：时间，表示波的当前时间
* φ：相位，表示波的起始位置

正弦波的图形是一个平滑的曲线，其形状类似于正弦函数。波峰和波谷分别对应于函数的最大值和最小值。

#### 3.1.2 正弦波在物理学中的应用

正弦波在物理学中有着广泛的应用，例如：

* **弹簧振动：**当一个弹簧被拉伸或压缩时，它会产生正弦波形的振动。
* **声波：**声波是由物体振动产生的，其波形通常是正弦波。
* **交流电：**交流电的电压和电流是正弦波形的。
* **电磁波：**电磁波，如无线电波和光波，也具有正弦波形的振幅。

### 3.2 傅里叶级数的表示和性质

#### 3.2.1 傅里叶级数的定义和收敛性

傅里叶级数是一种将周期函数表示为正弦波和余弦波的无穷级数。对于一个周期为 T 的函数 f(t)，其傅里叶级数为：

f(t) = a0/2 + ∑(n=1,∞) [an * cos(2πnt/T) + bn * sin(2πnt/T)]

其中：

* a0：常数项
* an：余弦项系数
* bn：正弦项系数

傅里叶级数的收敛性取决于函数 f(t) 的性质。如果 f(t) 是分段连续且分段光滑的，则其傅里叶级数一定收敛。

#### 3.2.2 傅里叶级数的应用

傅里叶级数在信号处理和图像处理中有着广泛的应用，例如：

* **信号分析：**傅里叶级数可以将信号分解成不同的频率分量，从而进行频谱分析。
* **图像压缩：**傅里叶级数可以将图像表示为一系列正弦波和余弦波，从而进行图像压缩。
* **解偏微分方程：**傅里叶级数可以用来解偏微分方程，如热方程和波方程。

# 4. 傅里叶变换与正弦波的关联

傅里叶变换和正弦波有着密切的联系，它们在信号处理、图像处理和工程应用中发挥着至关重要的作用。本章节将深入探讨傅里叶变换与正弦波之间的关联，并阐述其在实际应用中的意义。

### 4.1 傅里叶变换的正弦波表示

#### 4.1.1 正弦波的傅里叶变换

正弦波是一种周期性信号，其傅里叶变换是一个包含两个尖峰的离散谱。这两个尖峰分别位于正弦波频率的正负值处。

import numpy as np
import matplotlib.pyplot as plt

# 定义正弦波参数
amplitude = 1
frequency = 10
phase = 0

# 创建时间序列
t = np.linspace(0, 1, 1000)
signal = amplitude * np.sin(2 * np.pi * frequency * t + phase)

# 计算傅里叶变换
fft_signal = np.fft.fft(signal)

# 绘制频谱
plt.plot(np.abs(fft_signal))
plt.xlabel("Frequency")
plt.ylabel("Magnitude")
plt.show()

**代码逻辑分析：**

* `np.fft.fft(signal)`：计算信号的傅里叶变换，得到复数频谱。
* `np.abs(fft_signal)`：取频谱的绝对值，得到幅度谱。
* `plt.plot(np.abs(fft_signal))`：绘制幅度谱。

**参数说明：**

* `amplitude`：正弦波的振幅。
* `frequency`：正弦波的频率。
* `phase`：正弦波的相位。

#### 4.1.2 傅里叶变换的正弦波表示定理

傅里叶变换的正弦波表示定理指出，任何周期性信号都可以表示为一系列正弦波的叠加。傅里叶变换的输出频谱表示了这些正弦波的频率和幅度。

### 4.2 正弦波的傅里叶级数表示

#### 4.2.1 正弦波的傅里叶级数展开

正弦波也可以表示为傅里叶级数，即一组正交正弦波的叠加。傅里叶级数的系数表示了正弦波的振幅和相位。

# 正弦波的傅里叶级数展开
def fourier_series(signal, period):
    """
    计算信号的傅里叶级数展开。

    参数：
        signal: 输入信号。
        period: 信号的周期。

    返回：
        傅里叶级数展开的系数。
    """
    n = len(signal)
    coefficients = np.zeros(n, dtype=complex)

    for k in range(n):
        for i in range(n):
            coefficients[k] += signal[i] * np.exp(-1j * 2 * np.pi * k * i / n)

    return coefficients

**代码逻辑分析：**

* `np.exp(-1j * 2 * np.pi * k * i / n)`：计算正弦波的复指数项。
* `coefficients[k] += signal[i] * np.exp(-1j * 2 * np.pi * k * i / n)`：累加傅里叶级数的系数。

**参数说明：**

* `signal`：输入信号。
* `period`：信号的周期。

#### 4.2.2 傅里叶级数的正弦波表示定理

傅里叶级数的正弦波表示定理指出，任何周期性信号都可以表示为一组正交正弦波的叠加。傅里叶级数的系数表示了正弦波的振幅和相位。

# 5. 傅里叶变换与正弦波的工程应用

### 5.1 信号处理中的傅里叶变换

#### 5.1.1 频谱分析与滤波

傅里叶变换在信号处理中广泛应用于频谱分析和滤波。频谱分析通过计算信号的傅里叶变换，获得其频率成分的分布，从而识别信号中的特征频率。滤波则利用傅里叶变换将信号分解为不同频率成分，然后选择性地保留或去除特定频率范围的信号，实现信号的降噪、增强或提取。

#### 5.1.2 通信系统中的调制与解调

在通信系统中，傅里叶变换用于调制和解调信号。调制将信息信号调制到载波信号上，通过改变载波的频率或幅度来传输信息。解调则利用傅里叶变换将调制信号还原为原始信息信号。

### 5.2 图像处理中的正弦波

#### 5.2.1 图像增强与复原

正弦波在图像处理中应用于图像增强和复原。图像增强通过调整图像的频率成分，改善其对比度、亮度或锐度。图像复原则利用正弦波的正交性，将图像分解为正弦波分量，然后去除噪声或失真，重建清晰的图像。

#### 5.2.2 图像压缩与传输

正弦波还用于图像压缩和传输。图像压缩通过将图像分解为正弦波分量，然后丢弃高频分量，实现图像的压缩。图像传输则利用正弦波的正交性，将图像分解为正弦波分量，然后通过信道传输这些分量，在接收端重新合成图像。