正弦波在电气工程中的应用:交流电、谐波分析,掌握电气工程核心技术
发布时间: 2024-07-14 01:31:04 阅读量: 88 订阅数: 46 


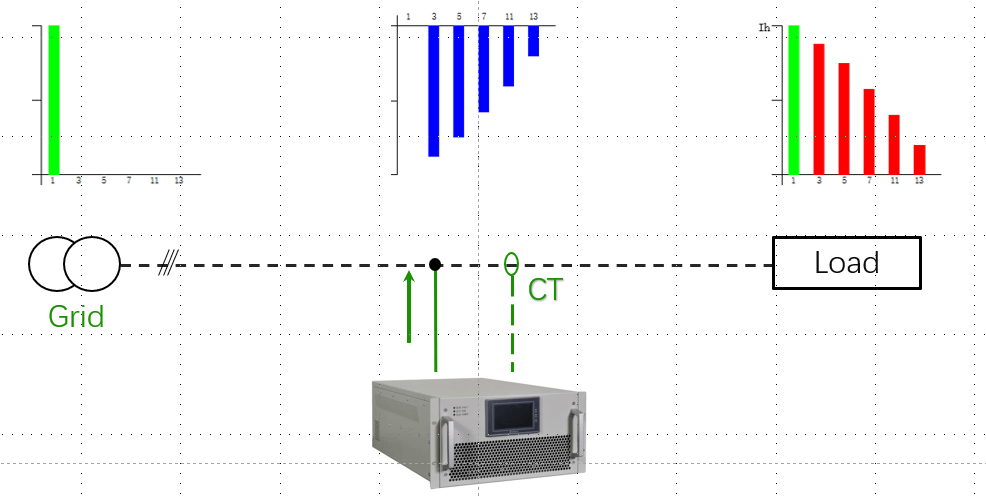
电力谐波检测分析与研究
# 1. 正弦波的基本概念和特性
正弦波是一种周期性波形,其振幅随时间以正弦函数变化。它在数学上表示为:
```
y(t) = A * sin(2πft + φ)
```
其中:
* A 为振幅,表示波形的最大值
* f 为频率,表示波形每秒重复的次数
* t 为时间
* φ 为相位角,表示波形在时间轴上的偏移
正弦波具有以下特性:
* 对称性:正弦波在时间轴上的正负部分对称
* 平均值为零:正弦波在整个周期内的平均值为零
* 傅里叶可分解:正弦波可以分解为一系列频率为基波频率整数倍的谐波
# 2. 正弦波在交流电中的应用
### 2.1 交流电的基本原理
#### 2.1.1 交流电的产生和传输
交流电是一种周期性变化的电流,其方向和大小随着时间而不断变化。交流电的产生主要依靠发电机,发电机利用电磁感应原理将机械能转化为电能。
发电机由定子和转子组成,定子是固定不动的,而转子可以旋转。定子绕组中通有直流电,产生磁场。转子绕组中没有通电,但由于电磁感应,当转子在定子磁场中旋转时,转子绕组中会产生感应电动势,从而产生交流电。
交流电的传输主要通过输电线路进行。输电线路由导线和绝缘材料组成,导线负责传输电能,绝缘材料负责防止电能泄漏。交流电的传输距离可以很长,这得益于交流电的变压器技术。
#### 2.1.2 交流电的特性和参数
交流电具有以下特性:
- **周期性:**交流电的波形是周期性变化的,即在一定时间内重复出现相同的波形。
- **频率:**交流电的频率是指每秒钟内波形重复出现的次数,单位为赫兹(Hz)。
- **幅值:**交流电的幅值是指波形中最大值或最小值的大小。
- **相位:**交流电的相位是指波形中某一点的时间位置,相位差是指不同波形之间的时间差。
交流电的参数主要包括电压、电流和功率。电压是指交流电两端之间的电位差,电流是指通过导体的电荷量,功率是指交流电传输的电能。
### 2.2 正弦波在交流电中的作用
#### 2.2.1 正弦波作为交流电的基波
正弦波是一种特殊的交流电波形,其波形是正弦函数。正弦波是交流电中最基本、最常见的波形,也是交流电系统分析的基础。
交流电的基波是指交流电中频率最低、幅值最大的分量。在大多数情况下,交流电的基波就是正弦波。正弦波基波的频率称为基波频率,幅值称为基波幅值。
#### 2.2.2 正弦波在交流电系统中的分析
正弦波在交流电系统分析中起着至关重要的作用。交流电系统中的电压、电流和功率都可以用正弦波来表示。
正弦波的分析方法主要包括傅里叶变换和频谱分析。傅里叶变换可以将正弦波分解为一系列正余弦函数,频谱分析可以显示正弦波中不同频率分量的幅值和相位。
通过对正弦波的分析,可以了解交流电系统中电压、电流和功率的变化规律,为交流电系统的设计、运行和维护提供基础。
**代码块:**
```python
import numpy as np
import matplotlib.pyplot as plt
# 定义正弦波参数
amplitude = 1 # 幅值
frequency = 1 # 频率
phase = 0 # 相位
# 生成正弦波数据
t = np.linspace(0, 10, 1000) # 时间范围
y = amplitude * np.sin(2 * np.pi * frequency * t + phase)
# 绘制正弦波
plt.plot(t, y)
plt.xlabel('时间 (s)')
plt.ylabel('幅值')
plt.title('正弦波')
plt.show()
```
**代码逻辑分析:**
1. 导入必要的库。
2. 定义正弦波的参数:幅值、频率和相位。
3. 使用 `np.linspace()` 函数生成时间范围。
4. 使用 `np.sin()` 函数生成正弦波数据。
5. 使用 `plt.plot()` 函数绘制正弦波。
6. 设置 x 轴和 y 轴标签以及标题。
7. 显示正弦波图。
**参数说明:**
* `amplitude`:正弦波的幅值。
* `frequency`:正弦波的频率。
* `phase`:正弦波的相位。
* `t`:时间范围。
* `y`:正弦波数据。
# 3.1 谐波的概念和产生
#### 3.1.1 谐波的定义和分类
**定义:**
谐波是指叠加在正弦波基波上的附
0
0





