MATLAB线性插值在图像处理中的魔法：图像缩放与变形，让图像焕发新生

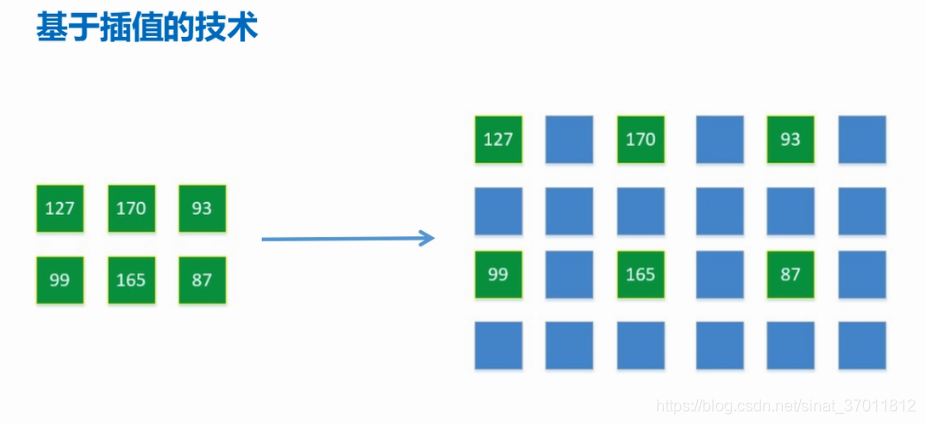
# 1. MATLAB线性插值的基本原理**

MATLAB线性插值是一种数值方法，用于估计给定数据集中的未知值。它基于这样一个假设：在两个已知数据点之间，函数值的变化是线性的。

线性插值公式为：

f(x) = y0 + (x - x0) * (y1 - y0) / (x1 - x0)

其中：

* `f(x)` 是未知值
* `x` 是未知点的自变量值
* `x0` 和 `x1` 是已知数据点的自变量值
* `y0` 和 `y1` 是已知数据点的因变量值

# 2. MATLAB线性插值在图像缩放中的应用

### 2.1 图像缩放的理论基础

#### 2.1.1 图像缩放的原理和方法

图像缩放是指改变图像的大小，使其适应不同的显示设备或需求。有两种主要的图像缩放方法：

- **上采样（放大）：**增加图像的分辨率，从而放大图像。
- **下采样（缩小）：**减少图像的分辨率，从而缩小图像。

#### 2.1.2 线性插值在图像缩放中的作用

线性插值是一种用于图像缩放的插值方法。它通过计算相邻像素之间的权重平均值来估计缩放后图像中每个像素的值。这种方法可以有效地平滑图像，减少缩放后的图像中的锯齿和失真。

### 2.2 MATLAB线性插值在图像缩放中的实践

#### 2.2.1 使用MATLAB实现图像缩放

MATLAB提供了`imresize`函数来实现图像缩放。该函数使用双线性插值算法，它是一种线性插值的扩展，考虑了相邻像素的四个角点。

% 读入图像
I = imread('image.jpg');

% 缩放图像为原来大小的2倍
I_scaled = imresize(I, 2);

% 显示缩放后的图像
imshow(I_scaled);

#### 2.2.2 不同插值方法的性能比较

除了双线性插值，MATLAB还提供了其他插值方法，如最近邻插值、双三次插值和Lanczos插值。这些方法在图像缩放中的性能不同，如下表所示：

| 插值方法 | 速度 | 质量 |
|---|---|---|
| 最近邻插值 | 最快 | 最差 |
| 双线性插值 | 中等 | 中等 |
| 双三次插值 | 较慢 | 良好 |
| Lanczos插值 | 最慢 | 最佳 |

选择合适的插值方法取决于图像缩放的特定要求。对于速度要求较高的应用，可以使用最近邻插值。对于质量要求较高的应用，可以使用双三次插值或Lanczos插值。

# 3. MATLAB线性插值在图像变形中的应用

### 3.1 图像变形的理论基础

#### 3.1.1 图像变形的类型和应用

图像变形是指对图像进行几何变换，以改变其形状、大小或位置。图像变形在图像处理和计算机视觉中有着广泛的应用，包括：

- **透视校正：**纠正由于相机透视造成的图像失真。
- **图像配准：**将两幅或多幅图像对齐，以便进行比较或融合。
- **图像扭曲：**对图像进行非刚性变换，以创建特殊效果或进行图像合成。
- **图像裁剪：**从图像中裁剪出感兴趣的区域。

#### 3.1.2 线性插值在图像变形中的作用

线性插值在图像变形中扮演着至关重要的角色。当图像进行变形时，原始像素位置会发生变化。为了获得变形后的图像，需要对原始图像中的像素值进行插值，以估计变形后位置的像素值。线性插值是最常用的插值方法之一，它通过相邻像素值的加权平均来估计插值值。

### 3.2 MATLAB线性插值在图像变形中的实践

#### 3.2.1 使用MATLAB实现图像变形

MATLAB提供了多种函数来实现图像变形，包括：

- **imwarp：**执行仿射、透视或自定义变形。
- **imresize：**缩放或旋转图像。
- **imcrop：**裁剪图像。