MATLAB线性插值在控制系统中的妙招：设计PID控制器，让系统稳定运行

# 1. MATLAB线性插值简介

MATLAB线性插值是一种强大的数值方法，用于估计给定数据集内未知点的值。它通过构建一条穿过已知数据点的直线来实现，并使用该直线来预测目标点的值。

MATLAB中线性插值的语法为：

y = interp1(x, y, xq, 'linear')

其中：

* `x`：已知数据点的x坐标
* `y`：已知数据点的y坐标
* `xq`：要插值的目标x坐标
* `linear`：指定使用线性插值方法

# 2. MATLAB线性插值在PID控制器中的应用

### 2.1 PID控制器的原理和结构

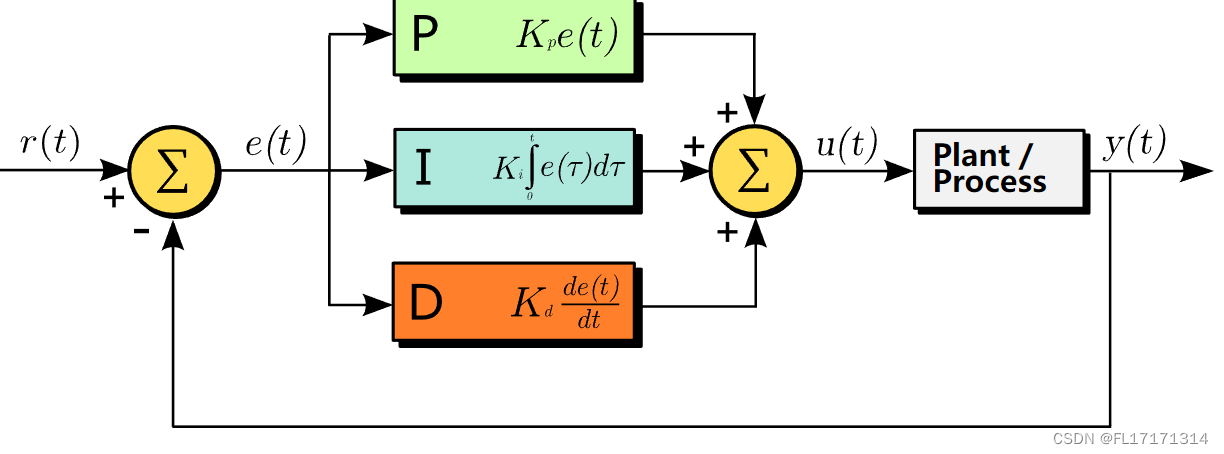
PID控制器是一种广泛应用于工业控制领域的反馈控制算法，其基本原理是根据系统的误差信号（期望值与实际值之差）来调整控制输出，从而实现系统的稳定和跟踪控制。PID控制器由比例控制、积分控制和微分控制三部分组成，各部分的作用如下：

**2.1.1 比例控制**

比例控制是最简单的控制方式，其控制输出与误差信号成正比，即：

u(t) = Kp * e(t)

其中：

* u(t) 为控制输出
* Kp 为比例增益
* e(t) 为误差信号

比例控制能够快速响应误差信号，但容易产生稳态误差（即当误差信号为零时，控制输出不为零）。

**2.1.2 积分控制**

积分控制通过累积误差信号来消除稳态误差，其控制输出与误差信号的积分成正比，即：

u(t) = Kp * e(t) + Ki * ∫e(t)dt

其中：

* Ki 为积分增益

积分控制能够消除稳态误差，但响应速度较慢。

**2.1.3 微分控制**

微分控制通过预测误差信号的变化率来提高控制系统的响应速度，其控制输出与误差信号的变化率成正比，即：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* Kd 为微分增益

微分控制能够提高响应速度，但容易产生振荡。

### 2.2 线性插值在PID控制器中的作用

线性插值是一种数学方法，可以根据已知的数据点来估计未知点的值。在PID控制器中，线性插值可以用于提高控制精度和增强系统鲁棒性。

**2.2.1 提高控制精度**

PID控制器的增益参数（Kp、Ki、Kd）对控制效果有很大的影响。传统的PID控制器采用固定增益，这可能会导致控制精度不高。线性插值可以根据系统的运行状态和误差信号的变化，动态调整增益参数，从而提高控制精度。

**2.2.2 增强系统鲁棒性**

系统鲁棒性是指系统在受到扰动或参数变化时保持稳定和性能的能力。传统的PID控制器对系统参数变化敏感，这可能会导致系统不稳定。线性插值可以根据系统的实际运行情况，调整增益参数，从而增强系统的鲁棒性。

# 3. MATLAB线性插值在PID控制器设计中的实践**

### 3.1 系统建模和参数辨识

#### 3.1.1 系统建模方法

系统建模是建立系统数学模型的过程，为PID控制器设计提供基础。MATLAB提供了多种系统建模方法，包括：

- **传递函数模型：**使用数学方程描述系统输入和输出之间的关系。
- **状态空间模型：**使用一组微分方程描述系统的状态和输出。
- **输入-输出数据模型：**使用输入和输出数据建立模型，无需明确的系统方程。

选择合适的建模方法取决于系统的复杂性和可用数据。

#### 3.1.2 参数辨识算法

参数辨识是确定系统模型中未知参数的过程。MATLAB提供了多种参数辨识算法，包括：

- **最小二乘法：**最小化模型输出与实际输出之间的误差平方和。
- **递归最小二乘法：**在线更新参数，适用于动态系统。
- **最大似然估计：**最大化模型输出与实际输出之间的似然函数。

选择合适的参数辨识算法取决于系统的特性和噪声水平。

### 3.2 PID控制器参数优化

#### 3.2.1 线性插值优化方法

线性插值是一种用于估计未知值的技术。在PID控制器优化中，线性插值可以用于估计控制器参数在不同操作条件下的值。

**步骤：**

1. 在不同的操作条件下收集系统数据。
2. 使用参数辨识算法确定每个操作条件下的PID控制器参数。
3. 使用线性插值估计其他操作条件下的参数。

#### 3.2.2 参数优化算法

MATLAB提供了多种参数优化算法，用于优化PID控制器参数，包括：

- **梯度下降法：**沿误差函数的负梯度方向迭代更新参数。
- **共轭梯度法：**一种更快的梯度下降法，利用共轭