MATLAB线性插值在科学计算中的妙用：求解微分方程，探索未知世界

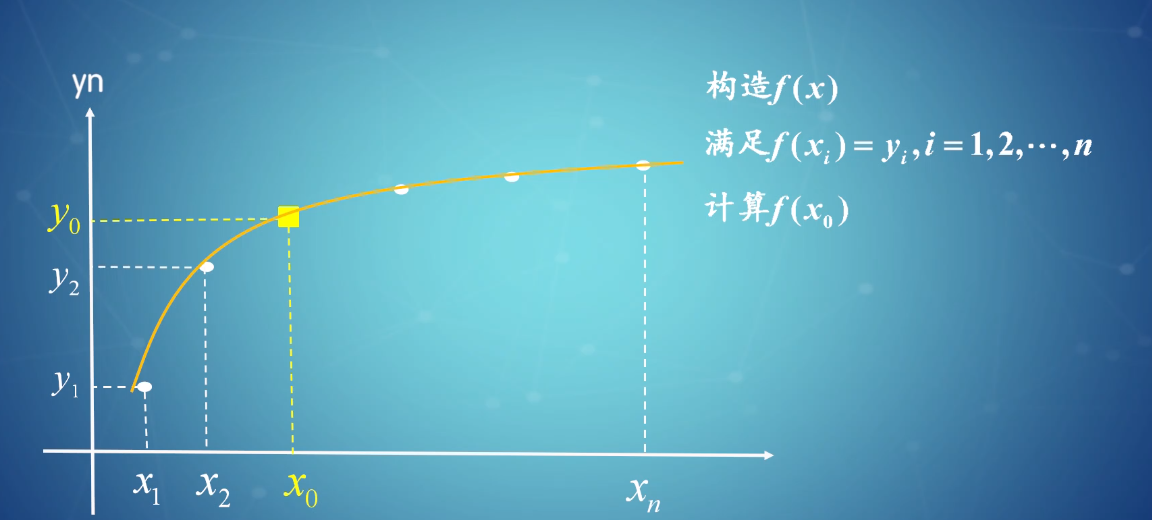
# 1. MATLAB线性插值的基础

线性插值是一种常用的数值分析技术，用于根据已知数据点估计未知数据点。MATLAB中提供了丰富的线性插值函数，可以方便地实现各种插值任务。

线性插值的基本原理是：对于给定的数据点(x1, y1)和(x2, y2)，如果要估计x∈[x1, x2]处的值y，则可以使用以下公式进行线性插值：

y = y1 + (y2 - y1) * (x - x1) / (x2 - x1)

其中，(x1, y1)和(x2, y2)是已知数据点，x是待估计的点，y是插值后的结果。

# 2. MATLAB线性插值在微分方程求解中的应用

MATLAB线性插值在微分方程求解中有着广泛的应用，它可以将微分方程转化为代数方程组，从而简化求解过程。本章节将介绍线性插值法在常微分方程和偏微分方程求解中的应用。

### 2.1 线性插值法求解常微分方程

常微分方程是一类描述未知函数对自变量一阶或更高阶导数关系的方程。线性插值法可以将常微分方程转化为代数方程组，从而简化求解过程。

#### 2.1.1 欧拉法

欧拉法是一种最简单的显式线性插值法，它将微分方程在当前点处的导数近似为前一点处的导数。欧拉法的具体公式如下：

y(n+1) = y(n) + h * f(x(n), y(n))

其中：

* `y(n)`表示第`n`个点的函数值
* `h`表示步长
* `f(x, y)`表示微分方程的右端函数

**代码块：**

% 定义微分方程的右端函数
f = @(x, y) x + y;

% 设置初始条件
x0 = 0;
y0 = 1;

% 设置步长
h = 0.1;

% 设置求解区间
x_span = [0, 1];

% 存储解
y_euler = zeros(1, length(x_span));
y_euler(1) = y0;

% 欧拉法求解
for i = 1:length(x_span)-1
    y_euler(i+1) = y_euler(i) + h * f(x_span(i), y_euler(i));
end

% 绘制解
plot(x_span, y_euler, 'b-o');
xlabel('x');
ylabel('y');
title('欧拉法求解常微分方程');

**逻辑分析：**

代码首先定义了微分方程的右端函数，然后设置了初始条件、步长和求解区间。接着，代码使用欧拉法求解微分方程，并存储解在`y_euler`数组中。最后，代码绘制了解。

#### 2.1.2 改进欧拉法

改进欧拉法是一种比欧拉法更精确的显式线性插值法，它将微分方程在当前点处的导数近似为前一点和当前点导数的平均值。改进欧拉法的具体公式如下：

y(n+1) = y(n) + h * (f(x(n), y(n)) + f(x(n+1), y(n) + h * f(x(n), y(n)))) / 2

**代码块：**

% 定义微分方程的右端函数
f = @(x, y) x + y;

% 设置初始条件
x0 = 0;
y0 = 1;

% 设置步长
h = 0.1;

% 设置求解区间
x_span = [0, 1];

% 存储解
y_improved_euler = zeros(1, length(x_span));
y_improved_euler(1) = y0;

% 改进欧拉法求解
for i = 1:length(x_span)-1
    y_improved_euler(i+1) = y_improved_euler(i) + h * (f(x_span(i), y_improved_euler(i)) + f(x_span(i+1), y_improved_euler(i) + h * f(x_span(i), y_improved_euler(i)))) / 2;
end

% 绘制解
plot(x_span, y_improved_euler, 'r-o');
xlabel('x');
ylabel('y');
title('改进欧拉法求解常微分方程');

**逻辑分析：**

代码与欧拉法求解类似，但改进了导数的近似方法。代码首先定义了微分方程的右端函数，然后设置了初始条件、步长和求解区间。接着，代码使用改进欧拉法求解微分方程，并存储解在`y_improved_euler`数组中。最后，代码绘制了解。

### 2.2 线性插值法求解偏微分方程

偏微分方程是一类描述未知函数对多个自变量偏导数关系的方程。线性插值法可以将偏微分方程转化为代数方程组，从而简化求解过程。

#### 2.2.1 显式方法

显式线性插值法将偏微分方程在当前点处的偏导数近似为前一点处的偏导数。显式方法的具体公式如下：

u(i, j+1) = u(i, j) + k * (f(i, j) - u(i, j))

其中：

* `u(i, j)`表示第`i`行第`j`列的函数值
* `k`表示步长
* `f(i, j)`表示偏微分方程的右端函数

**代码块：**

% 定义偏微分方程的右端函数
f = @(x, y) x + y;

% 设置初始条件
u0 = zeros(10, 10);
u0(1, :) = 1;

% 设置步长
k = 0.1;

% 设置求解区间
x_span = [0, 1];
y_span = [0, 1];

% 存储解
u_explicit = zeros(size(u0));
u_explicit(:, 1) = u0(:, 1);

% 显式方法求解
for i = 1:size(u0, 1)
    for j = 1:size(u0, 2)-1
        u_explicit(i, j+1) = u_explicit(i, j) + k * (f(x_span(i), y_span(j)) - u_explicit(i, j));
    end
end

% 绘制解
surf(x_span, y_span, u_explicit);
xlabel('x');
ylabel('y');
zlabel('u');
title('显式方法求解偏微分方程');

**逻辑分析：**

代码首先定义了偏微分方程的右端函数，然后设置了初始条件、步长和求解区间。接着，代码使用显式方法求解偏微分方程，并存