【R语言高级统计分析进阶】：贝叶斯方法在R中的应用与案例（数据先知）

# 1. 贝叶斯方法与R语言基础

在统计学和数据分析的世界里，贝叶斯方法提供了一种独特的概率框架来处理不确定性和推断。与传统的频率论方法不同，贝叶斯方法侧重于通过已知信息来更新对未知参数的信念。在这一章中，我们将介绍贝叶斯统计学的基础知识以及如何使用R语言这个强大的工具来实现这些概念。

## 什么是贝叶斯方法？

贝叶斯方法起源于18世纪，由托马斯·贝叶斯牧师提出，其核心思想是通过已有的先验信息和新的观测数据来动态更新对事件发生概率的认识。这种方法在处理不确定性和解释复杂数据方面表现出了巨大的潜力。

## R语言简介

R语言是一种专门用于统计分析和图形表示的语言和环境。它因其强大的社区支持、丰富的统计包和用户友好的接口而受到广泛欢迎。在贝叶斯分析中，R语言提供了诸如`rstan`、`MCMCpack`和`coda`等包，这些包使复杂计算变得简单和直接。

## 贝叶斯方法与R语言的结合

结合R语言进行贝叶斯分析，可以通过以下步骤实现：

1. **安装与加载贝叶斯相关的R包**：使用`install.packages()`函数安装贝叶斯分析相关的R包。
2. **定义先验分布**：在R中设置参数的先验概率分布，通常是根据历史信息或专家知识来完成的。
3. **构建似然函数**：似然函数表示在给定参数下观察到数据的概率。
4. **执行贝叶斯推断**：利用贝叶斯公式结合先验分布和似然函数来计算后验分布。
5. **后验分析**：分析后验分布来解释结果，这可能包括点估计、区间估计和模型诊断等。

理解贝叶斯方法与R语言的结合对于统计建模、数据分析和数据科学的实践者来说是极其重要的。在接下来的章节中，我们将深入探讨贝叶斯统计的核心概念，并通过实际案例展示如何在R中应用这些理论。

# 2. 贝叶斯统计的核心概念

## 2.1 概率论基础回顾

### 2.1.1 先验概率与后验概率

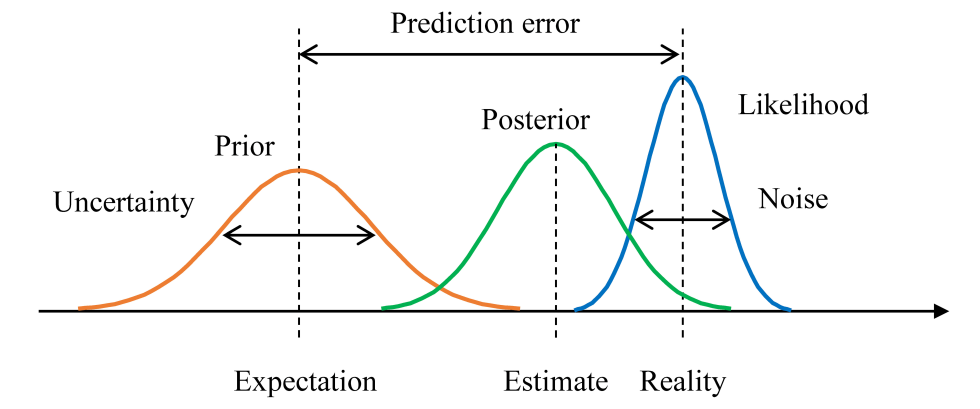
在贝叶斯统计中，先验概率（prior probability）是一个核心概念，它代表在观测数据之前，我们对某个假设发生的信念程度。这种信念可以是基于先前的经验、专家意见，或者任何其他可用的信息。贝叶斯推断的核心是使用先验概率和数据来更新我们的信念，并产生后验概率（posterior probability），即在观测数据之后对假设发生的信念程度。

例如，假设我们有一个硬币，并想要估计这个硬币正面朝上的概率。在没有其他信息的情况下，我们可能会假设正面朝上和反面朝上的概率各为0.5。但是，如果有人告诉我们这个硬币不太平衡，那么我们可能会倾向于认为正面朝上的概率大于0.5。这时，我们的先验知识就对先验概率产生了影响。

在贝叶斯推断中，先验概率和后验概率之间的关系由贝叶斯定理所描述。假定我们有一个先验概率分布\( P(H) \)和一个数据生成模型\( P(D|H) \)，其中\( H \)表示假设，\( D \)表示数据。根据贝叶斯定理，后验概率\( P(H|D) \)可以通过以下公式计算：

\[ P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)} \]

其中，\( P(D) \)是边缘似然（marginal likelihood），它是一个归一化常数，确保后验概率是一个合理的概率分布。

### 2.1.2 条件概率和贝叶斯定理

条件概率指的是在某些条件下事件发生的概率。贝叶斯定理是概率论中的一个定理，它描述了两个条件概率之间的关系。具体来说，它提供了由先验概率和似然（likelihood）来计算后验概率的方法。

贝叶斯定理的一般形式如下：

\[ P(H|D) = \frac{P(D|H) \cdot P(H)}{P(D)} \]

这里的\( P(H|D) \)是我们感兴趣的后验概率，\( P(H) \)是假设\( H \)在考虑数据之前成立的概率，即先验概率。\( P(D|H) \)是在假设\( H \)为真的情况下观测到数据\( D \)的概率，称为似然。最后，\( P(D) \)是观测到数据\( D \)的边缘概率。

为了直观理解这个定理，让我们考虑一个简单的例子。假设有一个疾病，其在总人口中的发病率为1%（这是先验概率）。有一种检测这种疾病的测试，其准确性为99%，即如果一个人患病，那么有99%的机会检测为阳性；如果一个人不患病，那么有99%的机会检测为阴性。现在，如果一个随机选出的人检测结果为阳性，他实际患病的概率是多少？这就是我们要计算的后验概率。

使用贝叶斯定理，我们可以计算出：

\[ P(病|阳性) = \frac{P(阳性|病) \cdot P(病)}{P(阳性)} \]
\[ P(病|阳性) = \frac{0.99 \times 0.01}{P(阳性)} \]

为了得到\( P(阳性) \)，我们需要考虑两种情况：一是真正患病的情况，二是未患病但测试错误的情况：

\[ P(阳性) = P(阳性|病) \cdot P(病) + P(阳性|健康) \cdot P(健康) \]
\[ P(阳性) = 0.99 \times 0.01 + 0.01 \times 0.99 \]

我们可以看到，即使测试的准确性非常高，但在一般人群中，当检测结果为阳性时，实际患病的概率并不高。这个计算结果说明了在评估测试结果时，先验概率和似然如何共同影响我们的信念。

## 2.2 贝叶斯推断原理

### 2.2.1 贝叶斯推断流程

贝叶斯推断是一种在给定观测数据的情况下，用来更新我们对模型参数或假设信念的方法。这个过程涉及几个步骤，遵循贝叶斯定理。以下是贝叶斯推断的基本流程：

1. **定义先验分布**：首先定义一个先验概率分布\( P(\theta) \)，这反映了在考虑任何数据之前对模型参数\( \theta \)的信念。

2. **建立似然函数**：接着建立一个似然函数\( P(D|\theta) \)，它表示在给定参数\( \theta \)的条件下观测到数据\( D \)的概率。

3. **计算后验分布**：然后根据贝叶斯定理计算后验分布\( P(\theta|D) \)，它代表了在观测数据\( D \)之后对参数\( \theta \)的新信念。

\[ P(\theta|D) = \frac{P(D|\theta) \cdot P(\theta)}{P(D)} \]

4. **进行参数推断**：最后，使用后验分布来进行参数推断。这可能包括计算后验均值、中位数、最高后验密度区间（Highest Posterior Density, HPD）或其他相关统计量。

### 2.2.2 贝叶斯推断与频率论的区别

贝叶斯推断和频率论是统计学中两种不同的推断范式。频率论统计学是基于长期频率解释的，它关注于重复实验中事件发生的频率。而贝叶斯推断侧重于概率的主观解释，即信念更新。

在频率论中，参数被视为固定的未知常数，统计推断的目标是确定这些未知参数的可能值。例如，频率论者会使用置信区间来表示某个参数可能的范围，而不是提供参数的概率分布。

相比之下，贝叶斯推断将概率视为表达不确定性的一种方式，并且允许在数据观测前后对参数的信念进行量化和更新。贝叶斯方法提供了一种更为直观的方式来处理不确定性和数据的信息。例如，在贝叶斯框架下，我们可以直接得出参数的后验分布，这是一个关于参数所有可能取值的概率分布，并且可以用于预测和决策。

一个关键的区别是频率论者避免使用主观概率，而贝叶斯方法则接受并使用主观概率。这意味着在贝叶斯推断中，先验概率的选择至关重要，因为它将影响后验分布的形态。

## 2.3 贝叶斯网络与图模型

### 2.3.1 贝叶斯网络概述

贝叶斯网络，又称信念网络，是一种用于表示变量间依赖关系的图形模型。它由一组节点和有向边组成，每个节点代表一个随机变量，边表示变量间的依赖关系。通过贝叶斯网络，我们可以表示变量间复杂的概率关系，并利用这种结构来简化概率计算。

在贝叶斯网络中，每个节点都有一个条件概率表（Conditional Probability Table, CPT），它列出了在给定其父节点条件下该节点取特定值的概率。这种结构允许我们通过局部信息来计算全局的概率分布。

贝叶斯网络的一个关键优势在于其能够表示因果关系。例如，如果我们认为“吸烟”（S）会导致“肺癌”（C），我们可以在这两个节点之间建立一个有向边。网络的这种因果表示对于专家系统和决策支持系统尤为重要。

### 2.3.2 图模型在R中的实现

在R语言中，可以使用多种库来实现和操作贝叶斯网络。一个流行的库是`gRbase`，它提供了一系列函数来创建和分析图模型。此外，`bnlearn`是一个专门用于学习和操作贝叶斯网络的强大库。

以下是使用`bnlearn`库在R中实现和分析贝叶斯网络的基本步