【LDA vs. PCA】：两者在数据降维中的对决与选择

# 1. 数据降维技术概述

数据降维是机器学习和数据分析中的一项关键技术，旨在减少数据集中的变量数量，同时尽可能保留原始数据中的重要信息。它在处理高维数据时显得尤为重要，因为高维数据往往会造成“维度的诅咒”，使得数据挖掘变得复杂和困难。通过降维，可以提高数据处理的效率、降低计算资源的需求，并且有时还能提升模型的性能和可解释性。常见的降维技术包括线性判别分析（LDA）和主成分分析（PCA），它们分别适用于不同的数据结构和问题领域。在后续章节中，我们将深入探讨这些技术的理论基础、对比分析、实际应用案例以及选择策略和优化方法。

# 2. LDA和PCA的理论基础

## 2.1 LDA的理论基础

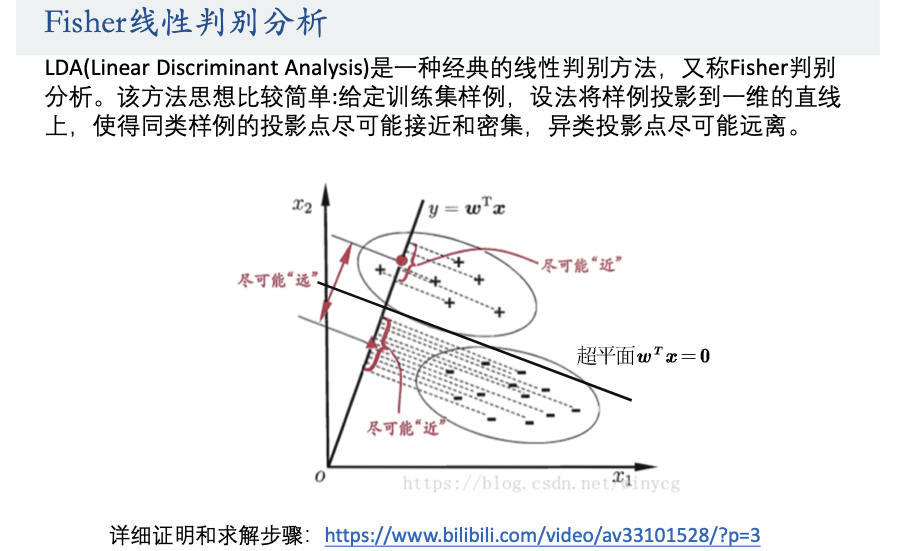
### 2.1.1 LDA的数学原理

线性判别分析（Linear Discriminant Analysis, LDA）是一种经典的统计学习算法，用于特征提取和数据降维。LDA的基本思想是在分类任务中，希望不同类别的样本在新的特征空间中有尽可能大的类间距离，而同一类别的样本间距离尽可能小。

LDA可以被视为一种监督学习的降维技术，它通过在特征空间中寻找一个投影方向（或多个方向），使得样本在此方向上投影后，同类样本之间的散度矩阵最小化，异类样本之间的散度矩阵最大化。数学上，这一问题可以转化为求解广义特征值问题。

假设有C个类别，每个类别有\(N_c\)个样本，\(x_{c,i}\)表示第c个类别的第i个样本。LDA计算类内散度矩阵\(S_W\)和类间散度矩阵\(S_B\)，其定义如下：

\[ S_W = \sum_{c=1}^C \sum_{i=1}^{N_c} (x_{c,i} - m_c)(x_{c,i} - m_c)^T \]

\[ S_B = \sum_{c=1}^C N_c (m_c - m)(m_c - m)^T \]

其中，\(m_c\)是第c类样本的均值向量，m是所有样本的均值向量。

LDA的目标是最大化类间散度矩阵\(S_B\)和类内散度矩阵\(S_W\)的行列式之比（或特征值之比），即求解如下的优化问题：

\[ J(W) = \frac{W^T S_B W}{W^T S_W W} \]

通过求解广义特征值问题 \(S_B W = \lambda S_W W\)，可以找到最佳的投影矩阵W，使得样本在新的特征空间中的类间距离最大化，类内距离最小化。

### 2.1.2 LDA的目标与应用场景

LDA的主要目标是在确保新特征空间中保持类别可分性的同时，减少数据的维度。其应用场景广泛，特别是在模式识别和机器学习领域，如：

- **文本分类**：在自然语言处理中，LDA可以用于文档分类，将文档向量化后的特征降至较低维度，以提高分类器的性能和效率。
- **生物信息学**：在基因表达数据分析中，LDA用于找出能够区分不同疾病状态的基因表达模式。
- **图像识别**：在处理具有多类别的图像数据时，LDA可以用于特征提取，使得图像的分类变得更加高效。

LDA在应用中通常需要满足一定的假设条件，比如类内分布接近于高斯分布，且具有相同的协方差矩阵。在实际应用中，当数据满足这些假设条件时，LDA效果较好。

## 2.2 PCA的理论基础

### 2.2.1 PCA的数学原理

主成分分析（Principal Component Analysis, PCA）是一种用于降维的统计方法，旨在找出数据集中的主要变量，这些变量能够解释数据的大部分变化。PCA通过正交变换将可能相关的变量转换为一组线性不相关的变量，这些变量称为主成分。

PCA的目标是找到数据的协方差矩阵（或相关矩阵）的特征值和特征向量，并按照特征值从大到小排列。这些特征向量构成了新的坐标轴，数据集在此坐标轴上的投影就是主成分。

首先，计算数据集的均值向量\(\mu\)和协方差矩阵\(C\)：

\[ C = \frac{1}{n} \sum_{i=1}^n (x_i - \mu)(x_i - \mu)^T \]

然后求解\(C\)的特征值问题：

\[ C v_i = \lambda_i v_i \]

其中，\(v_i\)是第i个特征向量，\(\lambda_i\)是对应的特征值。特征值\(\lambda_i\)表示了在第i个特征向量方向上的数据分散程度，通常按特征值大小对特征向量进行排序，最重要的特征向量（即对应最大特征值的向量）位于排序的最前面。

在进行降维时，选择前k个特征向量（主成分），并将原始数据投影到由这些特征向量构成的子空间中，从而实现数据降维。降维后的数据可以使用以下公式表示：

\[ Y = XW \]

其中，\(X\)是原始数据矩阵，\(W\)是选取的前k个特征向量构成的矩阵，\(Y\)是降维后的数据矩阵。

### 2.2.2 PCA的目标与应用场景

PCA的核心目标是数据降维，在降维过程中尽可能保留原始数据的方差信息。由于PCA保留了数据的主要方差，因此也保留了数据的主要特征。PCA广泛应用于数据预处理、可视化、噪声过滤等领域，尤其适用于高维数据的分析。

在实际应用中，PCA可能不适合所有类型的数据集。当数据集存在非线性结构时，PCA可能无法有效地提取信息。此外，PCA不考虑类别信息，是一种无监督的降维技术。

应用场景包括：

- **图像压缩**：在图像处理领域，PCA被用于减少图像数据的存储空间，同时尽可能保留图像的主要特征。
- **金融分析**：在金融领域，PCA用于风险管理和投资组合优化，帮助分析资产之间的关系。
- **生物信息学**：在基因组学研究中，PCA用于降维基因表达数据，帮助揭示样本之间的关系和变异。

为了在实际应用中更好地使用PCA，了解数据的统计特性和分布是很重要的。PCA对数据的缩放非常敏感，因此在应用PCA之前通常需要对数据进行标准化处理。

# 3. LDA与PCA的对比分析

## 3.1 线性判别与主成分分析的对比

### 3.1.1 算法目标差异

线性判别分析（LDA）和主成分分析（PCA）虽然都是数据降维技术，但它们在算法目标上有本质的区别。LDA旨在找到数据的最佳线性组合，以最大化不同类之间的区分度。也就是说，LDA通过在降维后的新空间中扩大类间距离，来提升分类器的性能。

PCA的目标则是找到数据的最主要的变化方向，这些方向依次代表了数据的最大方差。PCA不是为了区分不同的类别，而是为了保留数据的主要特征信息，减少数据维度的同时尽可能保持数据原有的结构。

### 3.1.2 算法步骤差异

LDA算法的步骤包括：
1. 数据标准化处理，确保各特征对结果的影响是均衡的。
2. 计算类内散度矩阵和类间散度矩阵。
3. 解决广义特征值问题，找到最优投影方向。

PCA算法的步骤包括：
1. 对数据进行中心化处理，使之均值为零。
2. 计算数据的协方差矩阵。
3. 计算协方差矩阵的特征值和特征向量。
4. 根据特征值大小，选择前k个最大的特征值对应的特征向量作为主成分。

## 3.2 实现细节与效率比较

### 3.2.1 计算复杂度

LDA在计算时需要考虑类内和类间的信息，其算法复杂度较高，尤其是当类别较多或样本量很大时。而且，LDA在进行特征抽取之前，需要先估计类条件概率密度函数，这在实际应用中可能需要复杂的模型或方法。

相比之下，PCA的计算复杂度相对较低，因为它只与数据的方差和协方差有关。PCA仅需要一个特征分解步骤，可以直接使用数学库中的算法来求解。

### 3.2.2 对数据分布的要求

LDA对数据分布有一定的要求，它假定同一类别的数据服从高斯分布，并且不同类别的协方差矩阵是相同的。当这些假设不成立时，LDA的效果可能不如预期。

而PCA对数据分布没有特别的假设，它不受类内分布的影响，仅关心数据的总体方