【LDA数学基石】：彻底理解线性判别分析的数学原理

# 1. 线性判别分析（LDA）概述

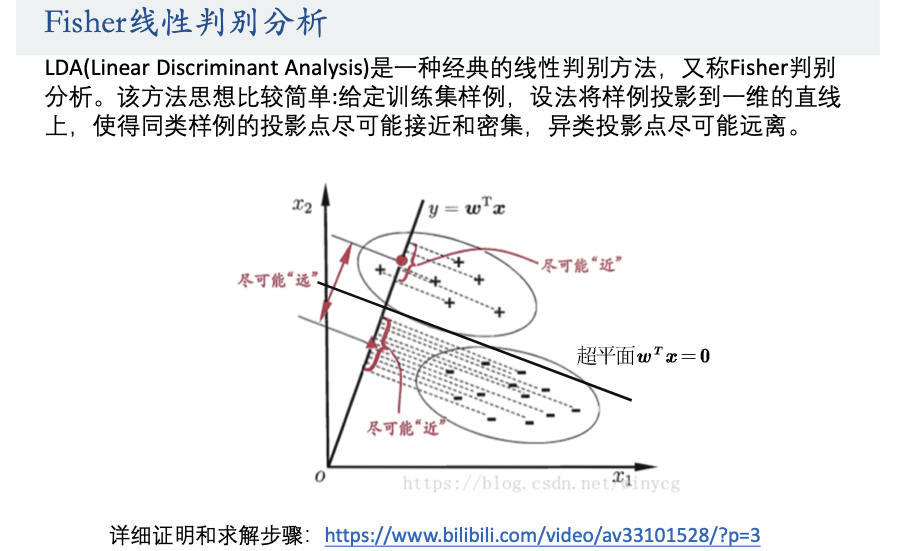
线性判别分析（Linear Discriminant Analysis，简称LDA）是一种经典的统计学习方法，广泛应用于模式识别和机器学习领域。LDA的核心思想是寻找一个线性组合的特征，这个组合能够最大化类别之间的区分度，同时最小化同类数据点之间的差异。作为一种降维技术，它不仅关注数据的类别标签，而且强调不同类别数据在新特征空间中的可分性。

LDA的提出，最初是为了实现降维，使得后续的分类器能够更高效地处理数据。它的优势在于其简洁的数学模型和良好的解释性，这使得LDA成为一个强大的工具，尤其在面对高维数据时，LDA能有效减少数据的复杂性并保持类别信息。

然而，LDA也有其局限性，比如它假设不同类别数据的分布是高斯分布，并且具有相同的协方差矩阵。这在实际情况中并不总是成立，因此，对LDA的理解和应用需要结合具体场景来考虑。后续章节我们将详细介绍LDA的理论基础，数学模型，几何解释，实现与优化方法，以及深入理解与未来展望。

# 2. 线性代数基础与概率论回顾

### 2.1 线性代数在LDA中的应用

#### 向量空间与基

向量空间是由向量组成的集合，这些向量必须满足加法和标量乘法的封闭性质。在LDA中，向量空间的概念是理解数据如何在多维空间中分布的关键。具体来说，LDA寻找的是一种投影，将数据点映射到一个低维空间，同时保留类别间的关键区分信息。

在数学上，设V为向量空间，若非空集合W满足以下条件，则称W为V的一个子空间：
- W对加法封闭：对任意 u, v ∈ W, 有 u + v ∈ W。
- W对标量乘法封闭：对任意 u ∈ W 和任意标量c，有 cu ∈ W。

基是向量空间的一个概念，它是线性无关向量的集合，任何向量空间中的元素都可以通过这个集合线性组合得到。基的选取对理解LDA中的类间离散度和类内离散度尤为重要，因为它们定义了类间和类内数据分布的几何结构。

flowchart TD
    V[向量空间 V] --> W[子空间 W]
    W --> B[基]

#### 特征值和特征向量

特征值和特征向量是理解数据分布和变换的关键工具。在线性代数中，对于一个方阵A，如果存在标量λ和非零向量v，使得Av=λv，则称λ为A的特征值，v为对应的特征向量。特征向量指明了数据在特定方向上的延伸程度，而特征值则量化了这种延伸的大小。

在LDA中，我们寻找的是一组特征向量，它们能够最大化类间离散度，同时最小化类内离散度。这些特征向量构成了LDA的投影轴，使得降维后的数据能够保持最大的类别区分度。

### 2.2 概率论基础

#### 随机变量与概率分布

随机变量是一个可以取不同值的变量，其取值结果遵循某种概率分布。在LDA中，随机变量常用来表示观测数据点。概率分布描述了随机变量取各个可能值的概率。理解不同概率分布的特性对于分析数据的统计特性至关重要。

- 离散随机变量：其可能的取值是有限个或可数无限多个，如掷骰子的结果。
- 连续随机变量：其取值构成一个连续区间或多个区间，如人的身高。

#### 多维随机变量及其分布

当一个随机变量由多个随机变量组合而成时，我们称之为多维随机变量。多维随机变量由多个变量的组合定义，并且每个变量都有自己的概率分布。多维随机变量的研究对于理解高维数据集特别重要。

对于两个离散随机变量X和Y，它们的联合概率分布给出了所有可能(X,Y)取值的概率。类似地，对于连续随机变量，可以定义联合概率密度函数。理解联合分布对于分析多个变量间的关系、进行多元统计分析以及LDA算法的理论推导都有重要意义。

### 2.3 多元高斯分布

#### 多元高斯分布的定义和性质

多元高斯分布（又称为多变量正态分布）是高维空间中正态分布的一种推广。若一个随机向量X的每一个分量都是正态分布的，那么X作为一个整体也服从多元高斯分布。多元高斯分布可以由均值向量和协方差矩阵完全确定。

- 均值向量μ：描述了分布的中心位置。
- 协方差矩阵Σ：描述了各个分量之间的相关性以及各自的变化范围。

多元高斯分布的概率密度函数由以下公式给出：

import numpy as np
from scipy.stats import multivariate_normal

# 定义多元高斯分布的参数
mu = np.array([0, 0])  # 均值向量
sigma = np.array([[1, 0], [0, 1]])  # 协方差矩阵

# 创建多元高斯分布对象
mvn = multivariate_normal(mean=mu, cov=sigma)

# 计算概率密度函数值
x = np.array([1, 1])
pdf = mvn.pdf(x)
print(pdf)

在上述Python代码中，我们定义了一个均值为零，协方差矩阵为单位矩阵的多元高斯分布，并计算了给定点(1,1)的概率密度值。

#### 多元高斯分布的参数估计

参数估计是统计学中的一个核心概念，指的是利用样本数据来估计概率分布的参数。在线性判别分析中，我们经常需要估计数据的均值向量和协方差矩阵。

对于样本均值，我们可以简单地用样本均值向量来估计。协方差矩阵的估计较为复杂，涉及到每个维度的方差以及维度间的协方差计算。以下是利用样本数据来估计多元高斯分布参数的示例代码：

import numpy as np
from numpy.linalg import det, inv
from scipy.stats import multivariate_normal

def estimate_parameters(X):
    mu = np.mean(X, axis=0)  # 计算样本均值
    diff = X - mu
    sigma = np.dot(diff.T, diff) / (len(X) - 1)  # 计算协方差矩阵
    return mu, sigma

# 假设X是一个样本矩阵，其中每一行是一个样本
X = np.array([
    [1.2, 3.5],
    [1.3, 3.6],
    [1.1, 3.4]
])

mu, sigma = estimate_parameters(X)
mvn = multivariate_normal(mean=mu, cov=sigma)
print(mvn.pdf(X))

在该代码中，我们首先定义了用于估计多元高斯分布参数的函数`estimate_parameters`，然后用一组样本数据计算了均值向量和协方差矩阵，并使用这些参数创建了一个多元高斯分布对象。最后，我们输出了每个样本点的概率密度值。

通过以上内容，我们理解了线性代数和概率论在LDA中的基础应用。这些基础知识为深入探讨LDA的数学模型和算法实现打下了坚实的基础。接下来的章节中，我们将进一步深入LDA的数学定义和优化问题，并探讨其在几何解释和实际应用中的具体内容。

# 3. LDA的数学模型

在深入探讨线性判别分析（LDA）的数学模型之前，我们必须了解其基本目标和假设。LDA是一种监督学习的降维技术，旨在找到一个线性组合的特征，以便在保证类间差异最大化的同时，最小化类内的数据点差异。我们将从数学定义开始，探索LDA的核心概念，然后深入其优化问题和数学证明。

## 3.1 LDA的数学定义

### 3.1.1 目标和假设

在LDA模型的构建中，我们首先定义一些基本的假设和目标。这些假设为：

- 数据集由多个类别组成，每个类别的数据点来自一个高斯分布。
- 不同类别的数据点的高斯分布具有相同的协方差矩阵。
- 我们的目标是找到一个投影方向，使得在该方向上的数据投影后，类间的距离尽可能大，类内的距离尽可能小。

根据这些假设，我们可以推导出一个判别函数，该函数能够最大化类间差异同时最小化类内差异。

### 3.1.2 判别函数的构造

判别函数通常是由两个部分组成：类间离散度矩阵（Between-class Scatter Matrix）和类内离散度矩阵（Within-class Scatter Matrix）。通过最小化类内离散度和最大化类间离散度，我们可以找到最优的投影方向。

数学表示上，假设我们有C个类别，每个类别的均值向量为μ_c，整体均值为μ，样本个数为n_c，总样本个数为N，则类间离散度矩阵和类内离散度矩阵分别为：

S_b =