贝叶斯优化助力超参数调优：机器学习模型性能提升25%的利器

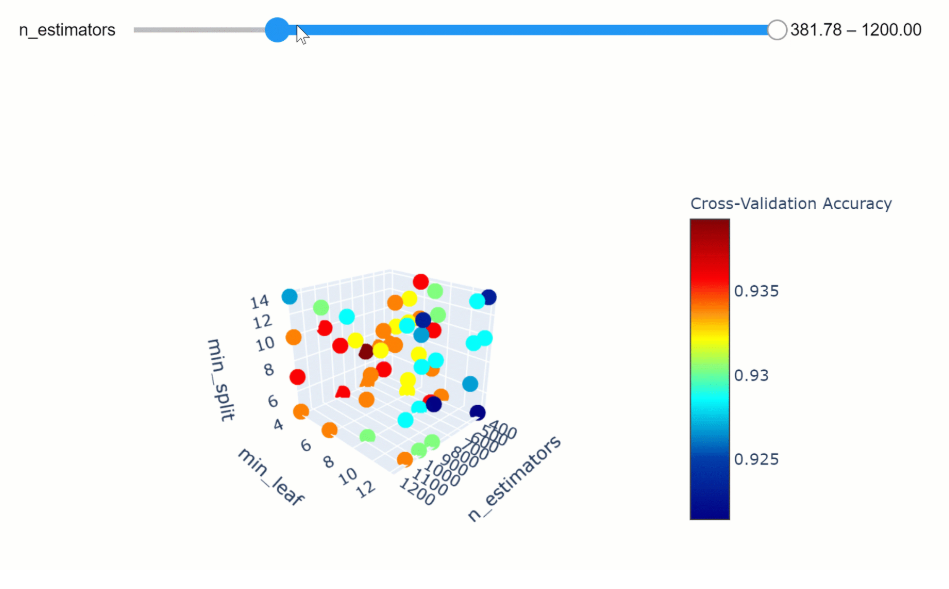
# 1. 贝叶斯优化简介

贝叶斯优化是一种基于贝叶斯统计的迭代优化算法，它通过构建目标函数的后验分布，指导后续的采样和优化过程。与传统优化方法相比，贝叶斯优化具有以下优点：

- **高效性：**贝叶斯优化通过利用先验知识和后验信息，减少了对目标函数的调用次数，从而提高了优化效率。
- **鲁棒性：**贝叶斯优化对目标函数的噪声和非连续性具有鲁棒性，可以有效地处理复杂和不确定的优化问题。
- **可解释性：**贝叶斯优化提供了目标函数后验分布的概率解释，帮助用户理解优化过程和结果的不确定性。

# 2. 贝叶斯优化理论基础

### 2.1 贝叶斯定理和先验分布

贝叶斯优化基于贝叶斯定理，它描述了在已知条件下事件概率的变化。在贝叶斯优化中，我们使用贝叶斯定理来更新对目标函数的信念，即后验分布。

后验分布表示在观察到一组数据后，目标函数的概率分布。它由先验分布和似然函数决定。

**先验分布**表示在观察任何数据之前，我们对目标函数的信念。它可以是任何概率分布，但通常选择一个反映我们对目标函数的先验知识的分布。

### 2.2 采样方法和后验分布

为了更新后验分布，我们使用采样方法从先验分布中生成样本。常用的采样方法包括：

- **Metropolis-Hastings 算法：**一种马尔可夫链蒙特卡罗 (MCMC) 方法，通过接受或拒绝从当前状态转移到新状态的提案来生成样本。
- **Gibbs 采样：**一种 MCMC 方法，通过一次更新一个变量来生成样本，同时保持其他变量不变。

通过采样，我们获得一组目标函数的样本，这些样本用于更新后验分布。后验分布表示在观察到这些样本后，我们对目标函数的信念。

### 2.3 优化目标和超参数空间

贝叶斯优化旨在找到优化目标函数的输入值，该函数可以是任何可计算的函数。优化目标通常表示为：

minimize f(x)

其中：

- `f(x)` 是目标函数
- `x` 是输入值

贝叶斯优化还涉及超参数空间，其中包含控制优化过程的超参数。这些超参数包括：

- **采样方法：**用于从先验分布中生成样本的方法
- **后验分布：**表示目标函数的概率分布
- **采集函数：**用于选择下一个要评估的输入值的方法

通过调整超参数，我们可以控制贝叶斯优化过程的效率和准确性。

**代码块：**

import numpy as np
from bayes_opt import BayesianOptimization

# 定义目标函数
def objective_function(x):
    return np.sin(x)

# 定义优化目标
optimizer = BayesianOptimization(
    f=objective_function,
    pbounds={"x": (-np.pi, np.pi)},
    random_state=1234
)

# 优化目标
optimizer.maximize(n_iter=10)

**逻辑分析：**

这段代码使用 `bayes_opt` 库执行贝叶斯优化。它定义了一个目标函数 `objective_function`，该函数返回 `x` 的正弦值。`pbounds` 参数指定了 `x` 的超参数空间，即从 -π 到 π。`random_state` 参数设置了随机数生成器的种子，以确保可重复性。`maximize` 方法使用贝叶斯优化算法最大化目标函数，执行 10 次迭代。

**参数说明：**

- `f`: 目标函数
- `pbounds`: 超参数空间
- `random_state`: 随机数生成器的种子
- `n_iter`: 迭代次数

# 3. 贝叶斯优化实践应用

### 3.1 机器学习模型超参数调优

#### 3.1.1 常见超参数类型

机器学习模型的超参数是控制模型学习过程和性能的配置参数。常见类型的超参数包括：

- **学习率：**控制模型更新权重时的步长。
- **正则化系数：**控制模型的复杂度，防止过拟合。
- **批大小：**指定每个训练批次中样本的数量。
- **网络架构：**指定模型中层数、节点数和连接方式。
- **激活函数：**指定隐藏层中非线性变换的类型。

#### 3.1.2 贝叶斯优化调优流程

贝叶斯优化用于调优超参数遵循以下流程：

1. **定义优化目标：**指定要优化的度量，例如模型准确率或损失函数。
2. **定义超参数空间：**指定超参数的取值范围和分布。
3. **初始化：**使用随机采样或专家知识初始化超参数集合。
4. **评估：**使用优化目标评估每个超参数组合的性能。
5. **更新后验分布：**基于评估结果，更新超参数的后验分布。
6. **获取新候选：**从后验分布中获取新的超参数候选，并评估其性能。
7. **重复步骤 4-6：**直到达到预定义的迭代次数或收敛标准。

### 3.2 复杂函数优化

#### 3.2.1 优化目标的定义

贝叶斯优化可用于优化复杂函数，这些函数可能是非凸、多模态或不可微的。优化目标可以是：

- **黑盒函数：**输入和输出之间的关系未知。
- **模拟函数：**通过模拟或仿真获得。
- **实验数据：**通过实验或测量获得。

#### 3.2.2 贝叶斯优化调优策略

用于复杂函数优化的贝叶斯优化策略包括：

- **高斯过程回归（GPR）：**使用高斯过程对目标函数进行建模，并预测新超参数组合的性能。
- **期望改进（EI）：**选择具有最高预期改进的超参数组合，即后验分布中比当前最优值更高的概率。
- **概率密度函数（PDF）：**选择具有最高概率密度函数的超参数组合，即后验分布中概率最高的点。

# 导入必要的库
import numpy as np
from bayes_opt import BayesianOptimization

# 定义优化目标函数
def objective_function(x):
    return np.sin(x) + np.random.normal(0, 0.1)

# 定义超参数空间
pbounds = {'x': (0, 2 * np.pi)}

# 创建贝叶斯优化器
optimizer = BayesianOptimization(
    f=objective_function,
    pbounds=pbounds,
    random_state=1,
)

# 优化超参数
optimizer.maximize(n_iter=100)

# 输出最佳超参数和目标值
print("最佳超参数：", optimizer.max['params'])
print("最佳目标值：", optimizer.max['target'])

**代码逻辑分析：**

* `objective_function` 定义了优化目标函数，它是一个带有噪声的正弦函数。
* `pbounds` 指定了超参数 `x` 的取值范围。
* `BayesianOptimization` 创建了贝叶斯优化器，指定了目标函数和超参数空间。
* `maximize` 方法执行优化过程，最大化目标函数。
* `n_iter` 参数指定了优化迭代的次数。
* `optimizer.max` 返回最佳超参数和目标值。

# 4. 贝叶斯优化进阶应用

### 4.1 多目标优化

#### 4.1.1 多目标优化问题定义

在实际应用中，优化问题往往涉及多个目标，这些目标之间可能存在冲突或相关性。多目标优化旨在同时优化多个目标，找到一组在所有目标上都表现良好的参数。

#### 4.1.2 贝叶斯优化多目标调优方法

贝叶斯优化可以扩展到多目标优化问题，通过以下方法：

* **帕累托优化：**帕累托优化是一种多目标优化方法，它寻找一组参数，使得在任何一个目标上进行改进都会导致其他目标恶化。帕累托最优解集称为帕累托