特征选择效果评估：关键指标与实用方法

# 1. 特征选择的重要性与挑战

在机器学习与数据分析中，模型的性能往往严重依赖于输入数据的质量。数据预处理的一个关键步骤就是特征选择，它涉及从原始数据集中挑选出与预测任务最相关的一组特征。这不仅提升了模型的泛化能力，减少了训练时间，还能避免过拟合，并提高了模型的可解释性。

然而，在实际应用中，特征选择的过程面临诸多挑战。数据集可能存在大量无关或冗余的特征，噪声和异常值也会影响特征选择的准确性。此外，特征间可能存在复杂的相互依赖关系，使得找出真正有用的特征组合变得更加困难。

为了克服这些挑战，数据科学家们采取了多种特征选择技术，包括但不限于过滤法、包裹法和嵌入法。每种方法都有其适用场景和优缺点，选择合适的方法进行特征选择对于最终模型的性能至关重要。

在后续章节中，我们将深入了解各种特征选择技术的理论基础、评估指标以及实用方法，并通过案例分析来展示特征选择在不同领域的应用和效果。

# 2. 特征选择的关键理论基础

## 2.1 特征选择在机器学习中的作用

### 2.1.1 特征选择的定义和目的

特征选择是指在机器学习和数据分析中，选择出那些对于模型性能提升最为关键的输入变量的过程。这一过程的目的是为了减少特征空间的维数，去除冗余和不相关特征，从而提高模型的训练效率和预测准确性，同时减少过拟合的风险。

特征选择不仅仅是维度的缩减，它也涉及到理解和解释数据。通过特征选择，可以更清晰地看到哪些变量是驱动结果的关键因素，这对于模型的解释性至关重要，尤其在一些需要解释模型预测结果的场合（如金融、医疗等行业）。

### 2.1.2 特征选择与模型性能的关系

特征选择与模型性能紧密相关。通过选择最有代表性的特征，可以构建出更加简洁、泛化能力强的模型。如果特征选择不当，可能会导致以下问题：

- 过拟合：包含无关特征的模型可能会在训练集上表现出色，但泛化到未知数据上时性能会急剧下降。
- 训练时间延长：不必要的特征会导致模型训练时间增加，特别是在使用复杂模型时。
- 降低模型解释性：大量的特征会使得模型的预测结果难以解释，影响决策过程。

因此，在进行机器学习任务时，合理的特征选择是提高模型性能和可解释性的关键步骤。

## 2.2 特征选择的方法分类

### 2.2.1 过滤法（Filter Methods）

过滤法是根据特征自身的统计特性进行特征选择的方法。这种方法不需要训练数据集以外的其他信息，简单、快速。常见的过滤法包括：

- 卡方检验（Chi-Squared Test）
- 相关系数（Correlation Coefficient）
- 互信息（Mutual Information）
- 方差分析（ANOVA）

过滤法的一个关键步骤是计算每个特征与目标变量之间的关系，然后根据这种关系的强度来选择特征。例如，卡方检验可以用来确定两个分类变量之间是否存在显著的统计相关性。过滤法的缺点是它可能忽略掉特征之间的交互作用。

### 2.2.2 包裹法（Wrapper Methods）

包裹法是将特征选择过程视为一个搜索过程，在这个过程中，选择的特征组合直接影响模型的性能。典型的包裹法包括：

- 递归特征消除（Recursive Feature Elimination, RFE）
- 前向选择（Forward Selection）
- 后向消除（Backward Elimination）

在RFE中，算法从完整的特征集开始，通过训练模型并评估特征的重要性来去除最不重要的特征，然后重复此过程直到达到所需的特征数量。包裹法的优点是它可以考虑到特征之间的相互作用，缺点是计算开销大，可能会导致过拟合。

### 2.2.3 嵌入法（Embedded Methods）

嵌入法是在模型构建过程中执行特征选择的方法。这意味着特征选择不是作为预处理步骤单独进行的，而是模型训练的一部分。常见的嵌入法有：

- LASSO回归（Least Absolute Shrinkage and Selection Operator）
- Ridge回归
- 决策树模型的特征重要性评分

嵌入法的一个主要优势是它在模型训练的同时进行特征选择，因此可以利用模型学习到的特征重要性。这种方法结合了过滤法和包裹法的优点，但选择合适的模型是关键。

## 2.3 特征选择的评估指标

### 2.3.1 准确性指标

准确性指标衡量的是模型预测正确的能力。最常用的准确性指标是准确率（Accuracy），它计算了正确分类的样本数占总样本数的比例。对于不平衡的数据集，准确率可能具有误导性，因此需要考虑其他指标。

### 2.3.2 信息量指标

信息量指标关注特征本身携带信息的能力，这些指标包括：

- 信息增益（Information Gain）
- 互信息（Mutual Information）
- 条件互信息（Conditional Mutual Information）

信息量指标通常用于过滤法，它们可以量化特征对于目标变量的预测能力。

### 2.3.3 稳健性指标

稳健性指标关注模型在面对数据波动时的稳定性。例如，特征的标准差或方差可以用来衡量数据的波动性。在特征选择中，稳健性指标有助于识别那些对于数据波动不太敏感的特征，从而增强模型的鲁棒性。

特征选择的理论基础为后续应用提供了坚实的基础。在下一章中，我们将深入探讨特征选择效果评估的关键指标，进一步理解如何衡量特征选择的好坏。

# 3. 特征选择效果评估的关键指标

特征选择效果的评估是机器学习和数据分析中一个不可或缺的环节。选择恰当的评估指标不仅能够帮助我们量化特征选择方法的有效性，而且能够指导我们做出更加合适的选择。本章节将深入探讨在特征选择效果评估中最为关键的几个指标，以及如何根据不同的数据集类型和问题类型应用这些指标。

## 3.1 评估指标的选择和解读

### 3.1.1 混淆矩阵与相关指标

混淆矩阵是一个用于描述分类模型性能的工具，它基于真实标签和模型预测标签来显示分类情况。对于二分类问题，混淆矩阵由四个部分组成：真正类（True Positive, TP）、假正类（False Positive, FP）、真负类（True Negative, TN）、假负类（False Negative, FN）。

在混淆矩阵的基础上，我们可以计算出多个指标，这些指标对于评估分类模型的性能至关重要：

- 准确率（Accuracy）：所有正确分类的样本占总样本的比例。

  Accuracy = \frac{TP + TN}{TP + TN + FP + FN}

- 精确率（Precision）：在所有预测为正的样本中，实际为正的样本的比例。

  Precision = \frac{TP}{TP + FP}

- 召回率（Recall）或真阳率（True Positive Rate, TPR）：实际为正的样本中被正确预测为正的样本比例。

  Recall = \frac{TP}{TP + FN}

- F1分数（F1 Score）：精确率和召回率的调和平均值，用于衡量模型的精确度和召回率的平衡。

  F1 Score = 2 \times \frac{Precision \times Recall}{Precision + Recall}

### 3.1.2 ROC曲线与AUC值

ROC（Receiver Operating Characteristic）曲线是通过将真正类率（TPR）与假正类率（False Positive Rate, FPR）绘制在同一张图上形成的曲线，其中FPR定义为FP/(FP + TN)。AUC（Area Under Curve）值表示的是在不同阈值下ROC曲线下的面积，其值的范围是0到1。AUC值越接近1，表示模型的分类能力越强。

### 3.1.3 F1分数与精确率和召回率

F1分数是精确率和召回率的调和平均值，它解决了精确率和召回率之间的平衡问题。当我们关注模型对正类的预测准确性时，F1分数是一个非常有用的指标。在数据集不平衡的情况下，单纯的准确率可能会因为类别不平衡而失去意义，此时F1分数能够提供更为客观的性能评估。

## 3.2 指标在不同数据集中的应用

### 3.2.1 不平衡数据集的评估策略

在不平衡数据集中，正负样本的比例相差很大，传统的准确率指标可能不能很好地反映模型性能。此时，可以使用F1分数、ROC曲线和AUC值等指标来评估模型。F1分数能够平衡精确率和召回率，是评估不平衡数据集上分类器性能的常用指标。ROC曲线和AUC值同样适用于不平衡数据集，它们不依赖于类别分布，因此可以作为更一般的性能度量。

### 3.2.2 多类别分类问题的评估

在多类别分类问题中，每个样本可以属于多个类别中的一个或多个。除了二分类问题常用的指标外，我们可以使用微平均（micro-averaging）和宏平均（macro-averaging）来计算精确率、召回率和F1分数。微平均是指先将所有类别中的TP、FP、FN值合并，再计算指标；而宏平均则是对每个类别独立计算指标后再求平均值。

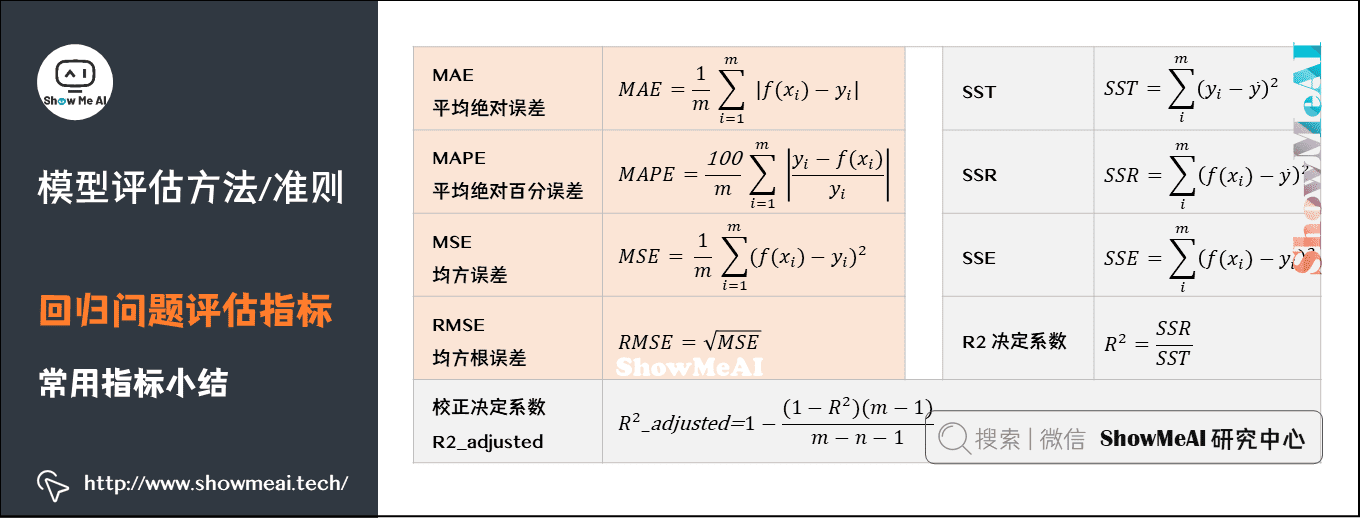
### 3.2.3 回归问题的评估指标

回归问题的评估指标关注的是预测值与真实值之间的差异。常用的回归评估指标包括：

- 均方误差（Mean Squared Error, MSE）：预测值与真实值差的平方的均值。
- 平均绝对误差（Mean Absolute Error, MAE）：预测值与真实值差的绝对值的均值。
- 决定系数（R²）：模型解释的变异量占总变异量的比例，用于评估模型的拟合程度。

不同的回归问题可能需要不同的评估指标，例如在预测房价时，可能会更关注MSE，而在预测汽车销量时，可能会更关注M