【并发编程】：递归在数据结构中的设计模式

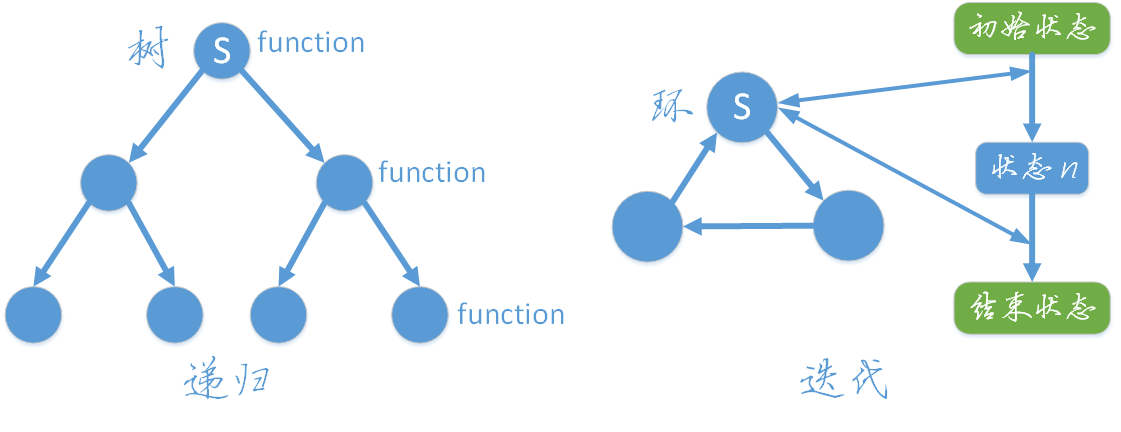
# 1. 并发编程基础与递归概念

在现代软件开发中，特别是在大数据处理和高性能计算领域，掌握并发编程和递归编程的概念是至关重要的。并发编程允许程序执行多条指令流，以此提高计算效率和响应速度；而递归编程则是指一种算法结构，它通过函数自己调用自己来简化问题的复杂度。

## 1.1 并发编程简介

并发编程是一种编程技术，用于构建能同时执行多个任务的程序。在多核处理器时代，通过并发，我们可以充分利用硬件资源，提高程序性能。并发通常涉及线程或进程的创建与管理，它们可以并行运行，但需要适当的同步机制来避免竞态条件和数据一致性问题。

## 1.2 递归的基本原理

递归是一种定义函数的方法，函数直接或间接地调用自身。每个递归函数都包含两个基本部分：基本情况（base case）和递归步骤（recursive case）。基本情况负责停止递归，而递归步骤则是将问题分解为更小的子问题，并调用自身来解决这些子问题。

# 一个简单的递归函数示例：计算阶乘
def factorial(n):
    if n == 0: # 基本情况
        return 1
    else: # 递归步骤
        return n * factorial(n-1)

在并发编程的环境中，递归函数的执行可能会遇到线程安全和性能优化的挑战。了解这些基础概念，为接下来深入探讨并发环境中递归的高级应用奠定了基础。

# 2. 递归在树形结构中的应用

### 2.1 树形结构的基本原理

#### 2.1.1 树的定义和特性

树是一种非线性数据结构，广泛应用于各种数据表示和算法设计中。它由节点（Node）和边（Edge）组成，其中节点表示数据元素，边表示节点之间的逻辑关系。树的特性包括：

- 根节点：树中的第一个节点，没有入边。
- 子节点：直接由某个节点通过边连接的节点。
- 父节点：连接到某个节点的上一个节点。
- 叶子节点：没有子节点的节点。
- 子树：任何节点的子节点，连同子节点的子节点等构成的树称为该节点的子树。

树的深度是树中节点的最大层数，而高度是根节点到最远叶子节点的最长路径上的边数。

#### 2.1.2 树的遍历方法

树的遍历方法主要有三种：

- 前序遍历（Pre-order Traversal）：首先访问根节点，然后遍历每一棵子树。
- 中序遍历（In-order Traversal）：先遍历左子树，再访问根节点，最后遍历右子树。
- 后序遍历（Post-order Traversal）：先遍历每一棵子树，最后访问根节点。

树的遍历可以使用递归方法实现，因为递归本质上是一种自顶向下或自底向上的遍历过程。

### 2.2 递归算法在树操作中的实现

#### 2.2.1 递归遍历二叉树

二叉树是一种特殊的树结构，每个节点最多有两个子节点。递归遍历二叉树的代码示例如下：

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None

def preorder_traversal(root):
    if not root:
        return []
    return [root.val] + preorder_traversal(root.left) + preorder_traversal(root.right)

def inorder_traversal(root):
    if not root:
        return []
    return inorder_traversal(root.left) + [root.val] + inorder_traversal(root.right)

def postorder_traversal(root):
    if not root:
        return []
    return postorder_traversal(root.left) + postorder_traversal(root.right) + [root.val]

在这段代码中，我们定义了一个简单的二叉树节点类 `TreeNode`，以及三个函数来分别实现前序、中序和后序遍历。每个函数都检查根节点是否为空，如果为空，则返回空列表；否则递归地对左右子树进行遍历。

#### 2.2.2 递归实现树的搜索与排序

在树形结构中，搜索和排序算法同样可以通过递归实现。搜索操作通常是通过递归在树的节点中查找特定值的过程。排序则涉及到特定类型的树，如二叉搜索树（BST），它有特定的性质：对于任意节点，其左子树上所有节点的值都小于该节点，右子树上所有节点的值都大于该节点。递归中序遍历二叉搜索树将得到一个有序的值序列。

### 2.3 并发环境下递归操作的设计

#### 2.3.1 并发控制与同步机制

在并发环境下，多个线程可能会同时访问和修改共享资源。为了防止数据竞争和保持数据一致性，需要引入并发控制和同步机制。常见的并发控制技术包括锁（如互斥锁、读写锁）、信号量、条件变量等。这些技术可以确保在任一时刻，只有一个线程能够执行递归树操作的临界区代码。

#### 2.3.2 递归树操作的线程安全实现

为了实现递归树操作的线程安全，可以使用锁来控制对节点的访问。例如，在二叉树的递归操作中，可以通过锁来确保在对节点进行修改时，不会有其他线程正在访问同一节点。下面是一个简化的线程安全的二叉树节点更新示例：

from threading import Lock

class TreeNode:
    def __init__(self, x):
        self.val = x
        self.left = None
        self.right = None
        self.lock = Lock()  # 为每个节点添加锁

def thread_safe_update(node, value):
    with node.lock:  # 使用节点的锁来确保线程安全
        node.val = value
        # 这里可以添加更多节点更新操作，保证操作的原子性

在这个示例中，我们为每个树节点添加了一个锁。在更新节点值的操作中，我们通过 `with` 语句获取节点的锁，确保了在修改节点值的过程中不会有其他线程干扰，保证了操作的线程安全。

递归树操作在并发环境下的设计需要考虑算法的正确性和性能。在实践中，可能需要结合具体的业务逻辑和系统需求，对锁的粒度和并发控制策略进行优化。

在下一章节中，我们将深入探讨并发编程中的递归算法优化，以提高性能并减少资源消耗。

# 3. 并发编程中的递归算法优化

## 3.1 递归算法的性能问题

### 3.1.1 时间复杂度分析

递归算法在解决问题时，可以表达得很简洁，但是其时间复杂度往往很高。考虑一个简单的例子，计算斐波那契数列中的第n项。

pu