【树遍历与搜索】：递归算法的详细解析与应用

# 1. 树遍历与搜索的基础概念

在计算机科学中，树结构是一种重要的非线性数据结构，用于模拟具有层级关系的数据。树的遍历与搜索是树操作中最基本的操作之一，它们是理解更复杂算法和数据结构的关键。本章节首先对树结构进行简要介绍，然后深入探讨树遍历与搜索的基本概念，为读者建立一个扎实的理论基础。

## 1.1 树的结构和特点

树是由节点组成的数据结构，其中每一个节点都有一个值以及若干个指向其子节点的引用。树具有以下特点：

- 根节点是树的起始节点。
- 子节点可以有零个或多个子节点，称为兄弟节点。
- 除根节点外，每个节点都有一个父节点。
- 没有父节点的节点称为叶节点。

## 1.2 遍历的定义

树遍历是指按照某种规则访问树中的每个节点一次且仅一次的过程。常见的遍历方法包括前序遍历、中序遍历和后序遍历。

- **前序遍历**：首先访问根节点，然后递归地前序遍历左子树，最后递归地前序遍历右子树。
- **中序遍历**：首先递归地中序遍历左子树，然后访问根节点，最后递归地中序遍历右子树。
- **后序遍历**：首先递归地后序遍历左子树，然后递归地后序遍历右子树，最后访问根节点。

## 1.3 搜索的意义

在树结构中，搜索是指在树中查找具有特定值或满足特定条件的节点的过程。搜索算法的效率直接影响到树结构操作的性能。树遍历与搜索算法在数据库索引、文件系统管理以及各种算法设计中发挥着重要作用。理解树遍历与搜索的基本概念，是掌握更高级树操作技术的前提。

通过本章内容的学习，读者应能够熟悉树的基本概念、遍历的分类以及搜索的含义。这将为后续章节中对递归算法、时间复杂度分析、树遍历与搜索算法实践等更高级话题的讨论打下坚实的基础。

# 2. 递归算法的理论基础

## 2.1 递归的定义和工作原理
递归是一种在解决问题时常用的方法，它允许一个函数直接或间接地调用自身。递归的关键在于找出问题的规模缩小后的相似子问题，并将原问题转化为这些子问题的解。

### 2.1.1 递归函数的构成
一个递归函数通常由两部分组成：基本情况（Base Case）和递归情况（Recursive Case）。
- **基本情况**是递归的终止条件，防止无限递归的发生。
- **递归情况**则是函数调用自身解决问题的子集。

递归函数的设计往往遵循以下步骤：
1. 定义函数的目标：它要解决什么问题？
2. 确定递归的终止条件：什么情况下不再需要递归？
3. 确定递归的公式：如何将原问题分解为子问题？
4. 确保递归的收敛性：递归过程是否一定能够朝着终止条件前进？

下面是一个经典的递归函数实现的例子：计算阶乘。

def factorial(n):
    if n == 0:  # 基本情况
        return 1
    else:  # 递归情况
        return n * factorial(n - 1)  # 函数自身调用

在这个例子中，`factorial(5)`将会逐步分解为`5 * factorial(4)`, `5 * 4 * factorial(3)`等，最终达到基本情况`factorial(0)`，并开始返回结果。

### 2.1.2 递归过程与堆栈
递归函数在执行过程中，每一次函数调用都会在调用栈上增加一层。当函数执行返回时，这一层就会从栈上移除。因此，递归过程可以看作是在堆栈上进行的操作。

在调用栈上，每个函数调用都保存着其局部变量和返回地址。当递归调用达到基本情况后，函数开始逐步返回，堆栈上的每一层都恢复并使用保存的状态继续执行。

由于堆栈空间有限，递归深度过大可能会导致栈溢出。因此，在设计递归算法时，我们必须注意递归深度的限制。

## 2.2 递归算法的时间复杂度分析
递归算法的时间复杂度通常根据递归的层数和每层处理的复杂度来确定。

### 2.2.1 时间复杂度基本概念
时间复杂度是对算法运行时间随输入数据增长而增长的量度。它通常表示为`O(f(n))`，其中`f(n)`是算法执行时间随输入大小`n`增加而增加的函数。

- **常数时间**：`O(1)`
- **线性时间**：`O(n)`，对于每增加一个输入元素，需要增加一个操作
- **对数时间**：`O(log n)`，算法处理需要的步骤随输入量的增加而对数级增长
- **线性对数时间**：`O(n log n)`
- **多项式时间**：`O(n^2)`, `O(n^3)`等，对于每个输入元素，算法需要执行多项式级别的操作

### 2.2.2 递归算法的时间复杂度计算
递归算法的时间复杂度取决于递归调用的次数和每次递归的复杂度。

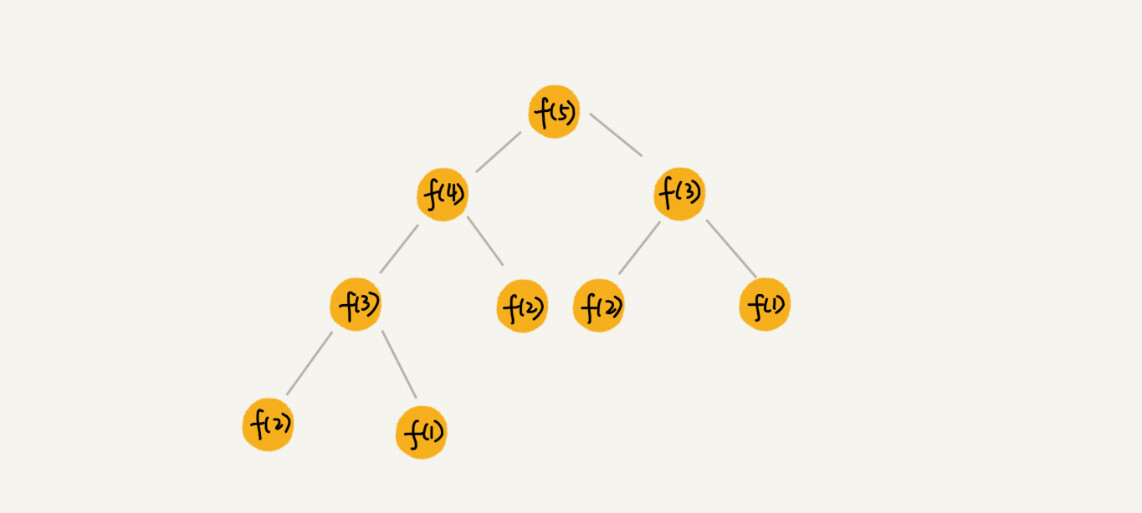
例如，考虑一个简单的递归函数计算斐波那契数列的第`n`项：

def fibonacci(n):
    if n <= 1:
        return n
    else:
        return fibonacci(n-1) + fibonacci(n-2)

这个函数的递归树会有`O(2^n)`个节点，因此时间复杂度为`O(2^n)`。这是一个指数级的时间复杂度，随着`n`的增加，计算量将迅速变得不可接受。

## 2.3 递归算法的优化方法
递归算法虽然简洁，但效率往往不高。存在一些优化方法可以提升递归算法的效率。

### 2.3.1 尾递归优化
尾递归是一种特殊的递归形式，在函数的最后一次操作中进行递归调用。尾递归可以被编译器优化，使得递归过程不需要在堆栈上增加新的帧，从而避免栈溢出的风险。

尾递归的条件：
- 递归调用是函数体中的最后一个操作
- 没有在递归调用之后需要执行的额外计算或资源释放

在支持尾递归的语言中，比如Scheme和Erlang，可以使用尾递归优化。但是需要注意的是，Python默认不支持尾递归优化。如果需要在Python中模拟尾递归，可以使用迭代代替递归。

### 2.3.2 迭代替代递归
递归到迭代的转换是一种常见的优化方法。通过循环结构替代递归函数，可以避免在调用栈上增加新的帧。

例如，可以将斐波那契数列的递归函数转化为迭代形式：

def fibonacci_iterative(n):
    a, b = 0, 1
    for _ in range(n):
        a, b = b, a + b
    return a

迭代版本的时间复杂度是`O(n)`，并且没有堆栈溢出的风险。这种方式比原始递归版本更加高效。

在优化递归算法时，需要注意递归和迭代两种方法在代码可读性和复杂性方面的权衡。有时候，递归的简洁和直观可以弥补其效率上的不足。在处理复杂问题时，理解递归的堆栈行为和递归树可以帮助我们更好地设计和优化算法。

递归算法是许多复杂计算的基础，理解其理论基础对于掌握更高级的算法至关重要。随着我们深入探讨树遍历和搜索算法，这些基础知识将成为理解更高级概念的基石。

# 3. 树的遍历算法实践

在计算机科学中，树结构是存储和组织数据的一种非常有效的模型。树的遍历算法则是对树结构进行系统化访问的重要手段，能够让我们遍历树中所有的节点。本章将详细介绍树的前序、中序和后序遍历的算法实践，并深入探讨递归遍历与非递归遍历的不同实现方式，最后通过应用案例展示遍历算法的实际运用。

## 3.1 树的遍历算法概述

树的遍历算法通常分为深度优先遍历和广度优先遍历两大类。深度优先遍历主要有三种形式：前序遍历、中序遍历和后序遍历；广度优先遍历通常指的是层序遍历。

### 3.1.1 前序遍历的实现

前序遍历是指在访问子树的所有节点之前先访问根节点。前序遍历的实现通常采用递归方法，代码实现如下：

class TreeNode:
    def __init__(self, value=0, left=None, right=None):
        self.val = value
        self.left = left
        self.right = right

def preorderTraversal(root):
    if not root:
        return []
    return [root.val] + preorderTraversal(root.left) + preorderTraversal(root.right)

在该代码段中，我们定义了一个简单的树节点类`TreeNode`，然后通过`preorderTraversal`函数来实现前序遍历。该函数首先检查当前节点是否为空，如果不为空，则先访问根节点，并递归访问左子树和右子树。

### 3.1.2 中序遍历的实现

中序遍历是指先访问根节点的左子树，然后