窗函数优化大揭秘：如何选择最佳窗口技术提升信号处理性能


参考资源链接：[胡广书《数字信号处理》第三版课后习题解答](https://wenku.csdn.net/doc/764xq846rz?spm=1055.2635.3001.10343)
# 1. 窗函数在信号处理中的作用

在数字信号处理领域，窗函数扮演着至关重要的角色，它们的主要作用在于改善频域的性能，同时也在时域内对信号进行平滑处理，以减少波形边缘的不连续性导致的频谱泄露问题。具体来说，窗函数通过加权信号数据，限定分析数据的时间段，从而使得信号具有良好的时频特性。应用窗函数可以有效控制信号处理过程中的旁瓣响应，减少噪声干扰，提高信号的频率选择性。

## 窗函数的基本功能

窗函数的基本功能包括：

- **改善信号的主瓣宽度**：通过选择合适的窗函数，可以得到更窄的主瓣宽度，提高信号的频率分辨率。
- **降低旁瓣水平**：不同的窗函数对旁瓣抑制的性能不同，选择合适的窗函数有助于减少旁瓣的干扰，提升信号质量。
- **抑制频谱泄露**：通过对信号进行加权处理，窗函数可以减小因信号截断而产生的频谱泄露。

理解窗函数的这些基本功能对于进行有效的信号处理至关重要。在接下来的章节中，我们将深入探讨窗函数的理论基础及其在不同应用场景中的应用和优化策略。

# 2. 基础窗函数理论与应用

### 2.1 窗函数的数学定义

在信号处理领域，窗函数（Window Function）是用于控制信号频谱泄露的关键工具。它是一种特定的数学函数，通常用于时域内对信号进行加权，以降低频谱分析时由于信号截断而产生的不希望的频谱泄露。

#### 2.1.1 离散傅里叶变换(DFT)与窗函数

当我们对一个有限长的时域信号执行离散傅里叶变换（DFT）时，我们实际上是在假设这个信号是以无限周期性重复的。在实际应用中，由于信号的长度是有限的，这种周期性假设会导致信号频谱的泄露，即信号的能量从它的实际频带泄漏到其他频带。窗函数的作用就是在时域内对信号进行加权，使得信号在时域的开始和结束时均为零，从而减少这种周期性假设所带来的频谱泄露。

DFT 定义如下：
\[ X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-j\frac{2\pi}{N}kn} \]
其中 \( x[n] \) 是时域信号，\( X[k] \) 是频域信号，\( N \) 是DFT的点数。

#### 2.1.2 窗函数的基本属性

窗函数有四个基本属性，分别是旁瓣水平、主瓣宽度、旁瓣衰减和主瓣宽度。这些属性决定了窗函数在频域中的性能表现。

- **旁瓣水平（Side-lobe Level）**：在主瓣之外，其他旁瓣的峰值电平。
- **主瓣宽度（Main-lobe Width）**：主瓣覆盖的频率范围，通常越窄越好，以提供更好的频率分辨力。
- **旁瓣衰减（Side-lobe Attenuation）**：主瓣到第一个旁瓣的幅度下降程度。
- **主瓣能量集中度**：信号能量集中在主瓣的程度。

### 2.2 常见基础窗函数介绍

#### 2.2.1 矩形窗、汉宁窗和汉明窗

在基础窗函数中，矩形窗、汉宁窗和汉明窗是最常用的。

- **矩形窗**：是最简单的窗函数形式，其效果相当于没有使用窗函数，因此具有最窄的主瓣宽度，但旁瓣水平高，频谱泄露严重。
- **汉宁窗**：通过一个余弦函数的模减半，得到了较好的旁瓣衰减，但主瓣宽度变宽。
- **汉明窗**：是在汉宁窗的基础上进一步优化，其主瓣宽度和旁瓣衰减之间达到了较好的平衡。

下面是三种窗函数的图形比较：

graph TD;
    A[矩形窗] -->|旁瓣水平高| B[频谱泄露];
    C[汉宁窗] -->|改进旁瓣衰减| D[频谱泄露减少];
    E[汉明窗] -->|进一步平衡| F[改善主瓣宽度和旁瓣衰减];

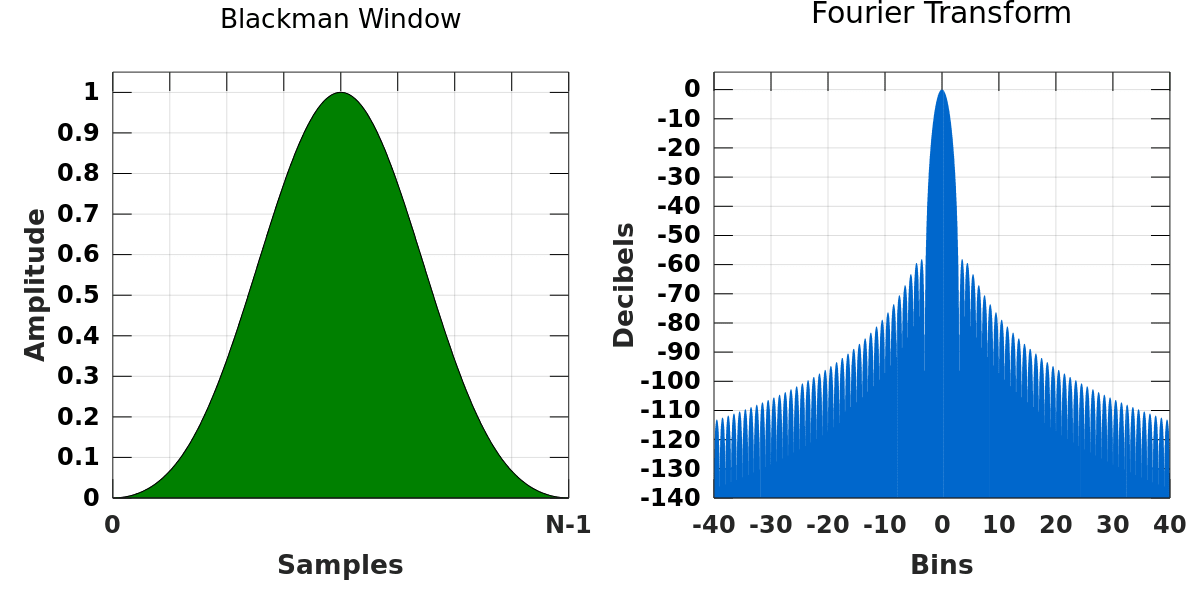
#### 2.2.2 布莱克曼窗和其他特殊窗函数

除了上述常见的窗函数外，布莱克曼窗和其他特殊窗函数也是信号处理中重要的工具。布莱克曼窗是在汉明窗的基础上进一步加权，以进一步降低旁瓣水平，但主瓣宽度会变得更宽。

特殊窗函数的例子包括高斯窗、凯撒窗等，它们在特定的应用场合具有优越的性能。

### 2.3 基础窗函数的性能比较

#### 2.3.1 频率选择性与旁瓣水平

在选择窗函数时，我们通常会权衡频率选择性和旁瓣水平。频率选择性是指窗函数对于频谱中不同频率成分的分辨能力，而旁瓣水平则直接影响到频谱泄露的程度。

- **频率选择性**：指的是窗函数能够将相邻频率成分区分开来的能力。理想的窗函数具有尖锐的主瓣宽度。
- **旁瓣水平**：描述了窗函数频谱中除主瓣外的其他旁瓣的电平。较低的旁瓣水平有助于减少频谱泄露的影响。

#### 2.3.2 时间分辨率和过渡带宽度

- **时间分辨率**：在时域中，窗函数决定了信号的分辨率。窗函数越短，时间分辨率越高。
- **过渡带宽度**：在频域中，过渡带宽度描述了窗函数从主瓣到第一个旁瓣的过渡速率。理想情况下，过渡带宽度越窄越好。

通过分析不同窗函数的数学表达式和频谱特性，我们可以根据具体需求选择合适的窗函数。例如，如果需要高时间分辨率，我们可能会选择短的矩形窗；如果频谱泄露是一个问题，汉宁窗或汉明窗可能是更好的选择。

在本章节中，我们深入了解了基础窗函数的定义、数学原理及其在信号处理中的作用。在实际应用中，对窗函数的选择将直接影响到信号分析的准确性和可靠性。下一章节将探讨如何根据不同的应用需求选择合适的窗函数，并介绍窗函数在实际中的应用案例。

# 3. 窗函数选择的实践指导

## 3.1 窗函数选择标准的理论分析

### 3.1.1 应用场景对窗函数性能的要求

在信号处理领域中，选择合适的窗函数是至关重要的。不同的应用场景对窗函数的性能有各自特定的要求。例如，在音频信号处理中，可能更关注频率选择性和旁瓣水平，因为这直接关联到信号的清晰度和抑制噪声的能力。而在雷达信号分析中，时间分辨率和过渡带宽度可能更为关键，因为这涉及到目标检测的准确性和速度。

### 3.1.2 窗函数参数调整的策略

窗函数的参数调整策略也是选择窗函数时的一个重要考虑因素。参数调整不仅影响信号处理的性能，也关系到算法的复杂度和计算成本。例如，增加窗函数的长度可以提高频率分辨率，但同时也会导致时间分辨率的下降，以及算法处理时间的增加。因此，在实际应用中需要根据具体需求进行权衡，找到最佳的参数组合。

## 3.2 常见应用案例分析

### 3.2.1 音频信号处理

在音频信号处理中，窗函数的选择对于提高音质和降低噪声至关重要。例如，使用汉宁窗可以减少频谱泄露，使得信号的频谱分析更加准确。而在抑制噪声方面，布莱克曼窗因其较低的旁瓣水平，能够有效地减少背景噪声的干扰，常用于音乐信号的处理。

import numpy as np
import matplotlib.pyplot as plt

# 创建一个信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)
signal = np.sin(2*np.pi*50*t) + 0.5*np.sin(2*np.pi*120*t)

# 应用汉宁窗
hann_window = np.hanning(len(signal))
signal_hann = signal * hann_window

# 应用布莱克曼窗
blackman_window = np.blackman(len(signal))
signal_blackman = signal * blackman_window

plt.figure(figsize=(12, 6))
plt.subplot(3, 1, 1)
plt.title("原始信号")
plt.plot(t, signal)

plt.subplot(3, 1, 2)
plt.title("汉宁窗处理后的信号")
plt.plot(t, signal_hann)

plt.subplot(3, 1, 3)
plt.title("布莱克曼窗处理后的信号")
plt.plot(t, signal_blackman)

plt.tight_layout()
plt.show()

### 3.2.2 雷达信号分析

在雷达信号处理中，对于距离和速度的精确测量要求窗函数具有良好的时间分辨率和频率分辨率。例如，使用凯泽窗可以减少信号的旁瓣，从而提高距离分辨率，这对于目标的精确定位非常重要。时间分辨率的提升则有助于快速响应，这对于高速运动目标的追踪至关重要。

### 3.2.3 无线通信中的应用

在无线通信中，窗函数的应用不仅限于提高信号质量，也用于频谱规划和资源分配。例如，在OFDM系统中，使用窗函数可以减少子载波间的干扰，提高系统的频谱效率。此外，窗函数还可以用于信号的调制和解调过程，其中参数的调整对于保证通信质量、抵抗干扰有着直接影响。

## 3.3 窗函数选择的软件实现

### 3.3.1 信号处理软件工具介绍

在实际应用中，软件工具的选择同样重要。例如MATLAB和Python都是广泛使用的信号处理工具。MATLAB提供了丰富的内置函数和工具箱，可以帮助快速实现窗函数的应用；Python则拥有强大的库支持，如SciPy和NumPy，可以灵活地自定义窗函数和进行复杂的数据处理。

### 3.3.2 实际编程实现与调优实例

在编程实现窗函数时，选择合适的库和函数是至关重要的。下面以Python为例，展示如何在实际编程中选择和应用窗函数。

from scipy.signal import get_window
import numpy as np
import matplotlib.pyplot as plt

# 定义一个窗函数
def apply_window(signal, window_type):
    # 获取窗函数
    window = get_window(window_type, len(signal))
    # 应用窗函数
    return signal * window

# 生成一个简单的信号
fs = 1000  # 采样频率
t = np.linspace(0, 1, fs, endpoint=False)
signal = np.sin(2*np.pi*50*t)

# 使用不同的窗函数处理信号
signal_hann = apply_window(signal, 'hann')
signal_blackman = apply_window(signal, 'blackman')

# 绘制结果
plt.figure(figsize=(12, 6))
plt.subplot(3, 1, 1)
plt.title("原始信号")
plt.plot(t, signal)

plt.subplot(3, 1, 2)
plt.title("汉宁窗处理后的信号")
plt.plot(t, signal_hann)

plt.subplot(3, 1, 3)
plt.title("布莱克曼窗处理后的信号")
plt.plot(t, signal_blackman)

plt.tight_layout()
plt.show()

通过以上代码，我们可以看到使用不同窗函数对信号进行处理的结果，并根据需要选择合适的窗函数。调优则涉及参数的微调，比如窗函数的长度和形状，以及信号本身的预处理步骤，以达到最优的信号处理效果。

| 窗函数类型 | 旁瓣水平（dB） | 过渡带宽度 |
|------------|----------------|-------------|
| 矩形窗 | -13 | 最窄 |
| 汉宁窗 | -32 | 稍宽 |
| 汉明窗 | -43 | 中等 |
| 布莱克曼窗 | -58 | 最宽 |

上表展示了不同窗函数在旁瓣水平和过渡带宽度方面的性能对比，可作为选择窗函数时的参考。

通过这些实例和分析，我们可以进一步理解窗函数在信号处理中的重要性和选择的复杂性。理论分析与软件实现的结合，为我们提供了一个实践窗函数选择的完整视角。

# 4. 先进窗函数技术探究

## 4.1 派生窗函数与混合窗技术

### 4.1.1 派生窗函数的构造方法

派生窗函数是基础窗函数通过数学变换和组合派生出的新型窗函数。例如，通过将两个基础窗函数进行加权和运算，可以得到混合窗函数。在数学术语中，派生窗函数一般可以表示为:

\[ W_{derived}(n) = \sum_{i} a_i \cdot W_i(n) \]

其中，\(W_i(n)\) 表示第i个基础窗函数，而 \(a_i\) 是一个加权系数。通过调整加权系数，可以得到不同性能特性的窗函数，从而满足特定应用的需求。

派生窗函数构造的关键在于合理选择基础窗函数和加权系数。通常这需要根据实际应用场景的需要来决定，比如在音频信号处理中，可能更关注旁瓣抑制，而在雷达信号分析中，则可能更看重主瓣宽度。为了得到最佳的性能，常常需要通过大量的实验和仿真来寻找最优的加权系数组合。

### 4.1.2 混合窗技术的原理和应用

混合窗技术通过将不同的窗函数进行组合，以此获得综合性能更优的窗函数。典型做法是在信号处理的不同阶段应用不同的窗函数。例如，在信号的预处理阶段使用一种窗函数以降低噪声影响，在主处理阶段使用另一种窗函数以优化频率选择性。

混合窗技术利用了不同窗函数的特定优势。比如，某些窗函数可能在时域上具有较好的集中性，而另一些则在频域上表现出更好的分辨率。当它们被适当地组合起来时，就能在时频域上同时获得较高的性能。

在具体应用中，混合窗技术可以根据信号的特性、应用需求以及实际的性能指标来定制。通过软件实现时，可以构建一个模块化的处理流程，每个模块采用不同的窗函数，组合起来实现整体的信号处理目标。

代码示例：

def mix_windows(signal, window1, window2, alpha):
    """
    A simple function to mix two windows for a signal.
    :param signal: Input signal array
    :param window1: First window function
    :param window2: Second window function
    :param alpha: Mixing parameter
    :return: Windowed signal
    """
    # Apply first window to the signal
    signal_windowed = signal * window1
    # Apply second window with a mixing parameter
    mixed_signal = signal_windowed * window2 * alpha
    return mixed_signal

参数`alpha`是控制两个窗函数混和程度的关键参数。根据具体应用，`alpha`可以是固定的，也可以是动态调整的。

## 4.2 可调节窗函数与自适应窗

### 4.2.1 可调节窗函数的参数化模型

可调节窗函数是一种参数化的窗函数，可以根据处理信号的不同特性动态调整其参数以达到最优的性能。这些参数化模型通常具有一定的灵活性，可以适应不同类型的信号和噪声环境。

典型的参数化模型如下：

\[ W(n, \theta) = f(n, \theta) \]

其中，\(n\) 是信号的离散采样索引，\(\theta\) 是一组可调节的参数，\(f\) 是一个定义了窗口形状的数学函数。通过改变参数 \(\theta\) 的值，可以得到不同的窗口形状。

举例来说，一些参数化模型可能会根据信号的噪声水平或信号强度来动态调整窗函数的形状。如果噪声水平较高，可能会降低旁瓣水平以减少噪声的影响；如果信号较强，则可能优先保证主瓣宽度，以提高信号的分辨率。

### 4.2.2 自适应窗函数的实时调整机制

自适应窗函数利用反馈机制实时调整其参数，以响应信号的变化。这种窗函数特别适合于信号特性会随时间变化的应用，如非平稳信号处理。

自适应窗函数的实时调整依赖于一套控制算法，该算法会根据实时信号分析的结果来调整窗函数的参数。常见的控制算法包括梯度下降法、神经网络自适应算法等。

代码示例：

class AdaptiveWindow:
    def __init__(self):
        self.params = [initial_value]  # Initial parameter values

    def adjust(self, signal, feedback):
        """
        Adjust window parameters based on feedback.
        :param signal: Input signal array
        :param feedback: Feedback information
        :return: Adjusted parameters
        """
        # Adjust parameters using feedback and control algorithm
        adjusted_params = control_algorithm(self.params, feedback)
        return adjusted_params

# Assume we have a control algorithm function
def control_algorithm(params, feedback):
    # Implement the control algorithm to adjust the parameters
    new_params = []
    for p in params:
        # Adjust each parameter based on the feedback
        new_p = p + feedback * learning_rate  # Simplified example
        new_params.append(new_p)
    return new_params

在这个示例中，`control_algorithm`代表自适应窗函数的控制算法，它根据实时反馈`feedback`和当前参数值`params`调整参数。真实的自适应窗函数调整算法可能会更加复杂，并且可能需要实时数据来不断调整。

## 4.3 窗函数在现代信号处理中的趋势

### 4.3.1 多分辨率分析与小波变换

随着对信号处理性能要求的不断提高，多分辨率分析逐渐成为窗函数研究的热点。小波变换是一种有效的多分辨率分析工具，其中窗函数作为小波基函数，在多分辨率分析中扮演着关键角色。

小波变换的核心思想是使用一组缩放和平移的小波函数来表示信号。这些小波函数本质上是窗函数在时频平面上的移动和缩放。通过这种方式，可以实现对信号的时频局部化分析，即在不同尺度上观察信号的细节。

多分辨率分析的关键是小波基的选取。理想的小波基具有良好的时频局部性，即其窗函数能够在时间和频率上同时具有较好的分辨率。小波窗函数的一个典型例子是高斯窗函数，它在时频平面上都具有很好的对称性和集中性。

### 4.3.2 深度学习在窗函数设计中的应用

近年来，深度学习技术在信号处理领域引起了革命性的变革。深度学习也被应用于窗函数设计中，以自动获取最适合当前信号特征的窗函数。

深度学习模型，尤其是卷积神经网络（CNNs）和递归神经网络（RNNs），可以被训练来预测窗函数的最优参数。通过将大量信号数据和对应的窗函数参数作为训练样本，深度学习模型可以学习到复杂信号特性和窗函数参数之间的非线性关系。

此外，生成对抗网络（GANs）也可以用来设计窗函数。通过训练一个生成器网络来生成窗函数，以及一个判别器网络来评估窗函数性能，GANs能够在训练过程中不断优化生成的窗函数，以达到最优的信号处理效果。

代码示例：

from keras.models import Sequential
from keras.layers import Dense, Conv2D, Flatten

# Define a simple neural network for window function optimization
model = Sequential()
model.add(Conv2D(32, kernel_size=(3, 3), activation='relu', input_shape=(None, None, 1)))
model.add(Flatten())
model.add(Dense(1, activation='linear'))  # Assuming a single parameter needs to be predicted

# Compile and train the model (a simple example)
model.compile(optimizer='adam', loss='mse')
model.fit(X_train, y_train, epochs=10, batch_size=32)  # X_train is the dataset, y_train is the window parameter

这个例子中展示了一个简单的卷积神经网络，其可以用来预测窗函数的参数。实际上，深度学习模型的设计和训练会根据具体问题的复杂度以及数据集的特性需要更多的考虑和调整。

通过上述的探讨，我们可以看到窗函数在现代信号处理技术中的重要地位和未来的发展趋势。这些高级技术的发展将进一步扩展窗函数的应用范围，提高信号处理系统的性能和灵活性。

# 5. 案例研究与性能测试

在信号处理领域，理论和实际应用之间往往存在巨大的鸿沟。本章旨在通过案例研究与性能测试，填补这一鸿沟，为读者提供实际应用中的窗函数优化实践和未来技术的发展方向。

## 5.1 窗函数优化的实验室测试

### 5.1.1 测试环境与工具设置

在进行窗函数优化的实验室测试时，创建一个受控的环境至关重要。这需要一个配置精确的计算机系统，安装有信号处理软件，例如MATLAB或Python，并配备高性能的数字信号处理器(DSP)或现场可编程门阵列(FPGA)。

- **软件工具**: 使用信号发生器软件来生成标准测试信号，例如正弦波、方波和噪声。
- **测试平台**: 搭建一个测试平台，比如使用NI LabVIEW进行数据采集与分析。
- **测量设备**: 配置频谱分析仪和示波器等硬件工具，用于记录信号在时域和频域的特性。

### 5.1.2 关键性能指标评估方法

性能评估的关键指标包括旁瓣抑制比(SLL)、主瓣宽度、过渡带宽度和综合性能指数等。具体步骤如下：

- **SLL和主瓣宽度**: 通过频谱分析仪记录窗函数处理后的信号频谱，计算旁瓣抑制比和主瓣宽度。
- **过渡带宽度**: 测量信号频率从主瓣到旁瓣过渡区的宽度。
- **综合性能指数**: 将上述参数综合成一个指数，以便在不同窗函数之间进行比较。

## 5.2 真实世界案例分析

### 5.2.1 工业环境中的信号处理挑战

工业环境中存在许多信号处理的挑战，例如设备振动监测、声纳系统和环境声音监测等。以振动监测为例，传感器采集到的信号往往包含大量的噪声，这需要窗函数来过滤掉不需要的频率分量。

- **挑战描述**: 工业振动信号往往具有非平稳特性，这要求窗函数具有良好的时间分辨率和频率选择性。
- **窗函数应用**: 应用布莱克曼窗处理信号，可以有效抑制噪声并保持信号的重要频率信息。

### 5.2.2 优化后的性能对比分析

通过实际应用优化后的窗函数，我们可以看到性能的显著提升。比较使用不同窗函数处理前后的信号，重点关注性能指标的改善程度。

- **数据记录**: 在应用窗函数优化前，记录传感器原始信号的频谱特性。
- **处理与比较**: 使用窗函数处理信号后，再次记录信号的频谱特性，并与原始数据进行对比。
- **结果展示**: 展示优化前后信号的频谱图，可以清晰地看到旁瓣水平的降低和主瓣宽度的调整。

## 5.3 未来窗函数技术的发展方向

### 5.3.1 新型窗函数的设计理念

随着技术的进步，未来的窗函数设计将更加注重灵活性和适应性。设计新型窗函数时，将考虑以下几个方面：

- **动态调整能力**: 新型窗函数将拥有在处理过程中动态调整其参数的能力。
- **多目标优化**: 设计时不仅要考虑降低旁瓣水平，同时也要平衡主瓣宽度、过渡带宽度等性能指标。

### 5.3.2 窗函数技术在量子计算中的潜力讨论

量子计算为窗函数技术带来了新的发展潜力。在量子计算中，信号处理不仅限于经典信息处理，还包括量子态的操控和测量。以下是几个可能的发展方向：

- **量子窗函数**: 研究如何将窗函数的概念应用于量子态的处理，例如量子傅里叶变换(QFT)。
- **量子优势**: 探索窗函数在量子计算中的应用是否能带来传统计算无法比拟的优势。

通过本章的探讨，我们不仅能够理解窗函数在真实世界中的应用和性能测试，还能够对未来的技术发展方向有一个大致的预期。这为我们提供了在不断变化的技术环境中保持竞争力的洞察力。