MATLAB生物统计进阶秘籍：解锁数据分析的高级技巧

目录
1. MATLAB在生物统计中的应用基础

1.1 MATLAB界面和基本操作
1.2 数据类型和基本函数
1.3 简单统计分析示例

2. 高级数据处理技术

2.1 数据清洗和预处理

2.1.1 缺失数据的处理策略

删除含有缺失值的行
使用均值或中位数填充

2.1.2 异常值的识别与处理

删除异常值
使用变换方法

2.2 多维数据分析

2.2.1 主成分分析（PCA）

使用PCA进行数据降维

2.2.2 聚类分析技术

K-means聚类
层次聚类

2.3 高级数据可视化

2.3.1 热图和箱线图的绘制

热图绘制
箱线图绘制

2.3.2 交互式数据可视化工具

创建交互式图表

3. 生物统计模型构建与优化

3.1 统计模型的选择与构建

3.1.1 线性回归与逻辑回归
3.1.2 生存分析模型

3.2 模型评估与验证

3.2.1 模型的交叉验证方法
3.2.2 ROC曲线与AUC值分析

3.3 高级统计分析技术

3.3.1 方差分析（ANOVA）与协方差分析
3.3.2 时间序列分析

4. 生物信息学中的应用实例

4.1 基因表达数据分析

4.1.1 微阵列数据处理
4.1.2 转录组数据分析

5. MATLAB生物统计的进阶拓展

5.1 集成其他编程语言

5.1.1 MATLAB与R语言的交互
5.1.2 MATLAB与Python的数据交换

5.2 生物统计软件包的开发

5.2.1 自定义函数与工具箱的创建
5.2.2 算法封装与用户界面设计

5.3 人工智能在生物统计中的应用

5.3.1 机器学习技术概述
5.3.2 MATLAB在生物医学领域的深度学习应用案例

1. MATLAB在生物统计中的应用基础
MATLAB是一种高性能的数值计算环境和第四代编程语言，广泛应用于工程计算、数据分析、算法开发等多个领域。在生物统计中，MATLAB以其强大的矩阵运算能力、丰富的工具箱以及直观的编程特点，成为生物医学研究者的重要工具。
1.1 MATLAB界面和基本操作
MATLAB的用户界面由命令窗口、编辑器、工作空间、路径和工具箱等构成，初学者需要熟悉这些基本组成部分来有效使用MATLAB。打开MATLAB后，用户可以在命令窗口中直接输入命令进行操作，或编写脚本(.m文件)来运行更复杂的程序。
1.2 数据类型和基本函数
MATLAB支持多种数据类型，包括标量、向量、矩阵和多维数组等。生物统计中的数据处理往往涉及向量和矩阵的操作，因此掌握基本的数学运算函数是必要的。例如，sum() 函数可以用于求和，mean() 用于求平均值，sort() 用于排序，以及 size() 用于获取数据的维度信息。
1.3 简单统计分析示例
下面是一个使用MATLAB进行简单生物统计分析的例子：
% 假设data为一组生物样本的表达量数据data = [2.1, 4.5, 3.9, 4.1, 5.0];% 计算平均值mean_value = mean(data);% 计算标准差std_dev = std(data);% 显示结果disp(['平均值: ', num2str(mean_value)]);disp(['标准差: ', num2str(std_dev)]);登录后复制
通过以上章节，我们可以看出MATLAB为生物统计提供了强大的工具和方法，使得研究人员能够高效地完成数据处理与分析任务。接下来章节将深入探讨MATLAB在高级数据处理、统计模型构建和优化等方面的应用。
2. 高级数据处理技术
2.1 数据清洗和预处理
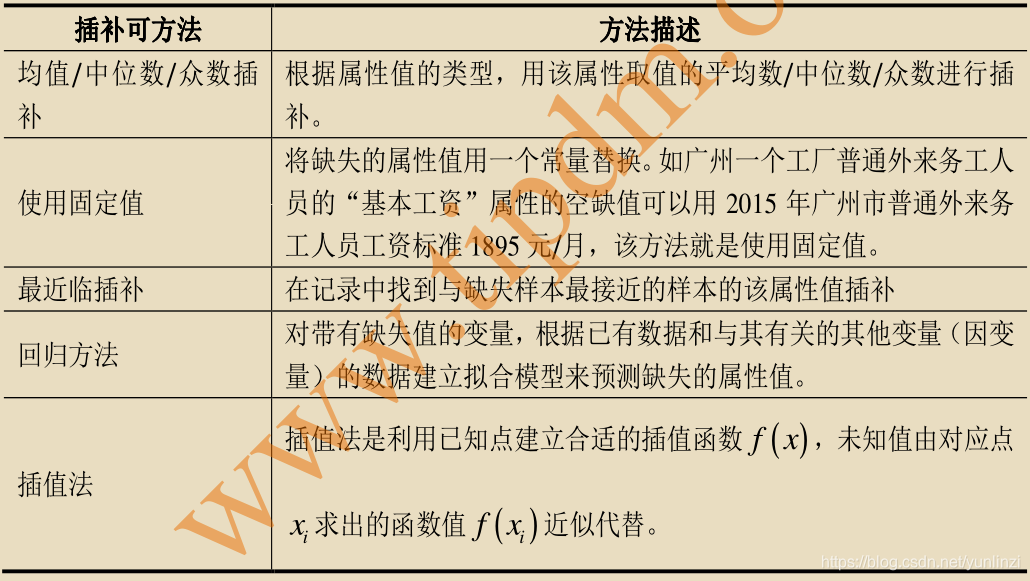
2.1.1 缺失数据的处理策略
在数据分析过程中，处理缺失数据是一项重要任务，因为缺失数据可能会影响统计分析的准确性和可靠性。在MATLAB中，我们可以使用多种方法来处理缺失数据。常见的策略包括删除含有缺失值的行、使用均值或中位数填充缺失值、或者采用更复杂的插补方法，比如基于模型的插补。
删除含有缺失值的行
最简单的方式是删除所有含有缺失值的行。在MATLAB中，可以使用rmmissing函数来实现这一点。以下是一个简单的例子：
% 假设A是一个包含缺失值的矩阵A = [1, NaN, 3; 4, 5, NaN; NaN, 7, 9];% 删除含有缺失值的行A_clean = rmmissing(A, 'Rows', 'all');登录后复制
删除缺失值的行可能会导致数据量大幅减少，特别是当数据集中有很多行含有缺失值时。因此，在实际操作中，只有当缺失值较少时才推荐使用这种方法。
使用均值或中位数填充
在许多情况下，我们可以通过填充缺失值来保持数据集的完整性。通常，我们会用整个列的均值或中位数来替换缺失值。在MATLAB中，可以利用fillmissing函数实现这一点：
% 使用均值填充缺失值A_filled_mean = fillmissing(A, 'mean');% 使用中位数填充缺失值A_filled_median = fillmissing(A, 'median');登录后复制
填充方法简单且易于实现，但它可能会降低数据的方差，并且不适合有模式存在的数据。例如，如果数据的缺失不是随机的（如数据录入错误或测量问题导致的缺失），那么简单地使用均值或中位数填充可能会引入偏差。
2.1.2 异常值的识别与处理
异常值是数据集中偏离正常范围的观测值，它可能是由于测量误差或随机波动导致的。处理异常值的策略包括删除异常值、使用基于统计的处理方法或者采用变换方法以减少异常值的影响。
删除异常值
最直接的方法是删除那些被识别为异常值的数据点。MATLAB提供了一些函数和统计方法来帮助我们识别异常值，例如Z分数法。Z分数表示一个数据点距离均值的标准差数量，通常将Z分数大于3或小于-3的数据点视为异常值。
% 假设B是一个数据集B = [10.5, 12.3, 11.4, 30, 12.8];% 计算均值和标准差mean_B = mean(B);std_B = std(B);% 标准化数据并找出异常值Z_scores = (B - mean_B) / std_B;outliers = B(abs(Z_scores) > 3);% 删除异常值B_clean = B(abs(Z_scores) <= 3);登录后复制
删除异常值可能会导致信息丢失，尤其是当数据集中异常值是由于有意义的变化造成的时。因此，在删除之前应当谨慎考虑。
使用变换方法
对于一些具有明显趋势或波动的异常值，我们可以通过变换方法来减少其影响。例如，对数变换、平方根变换或Box-Cox变换等可以减少数据的偏斜性，从而弱化异常值的影响。
% 使用对数变换B_transformed = log(B);登录后复制
变换方法能够保持数据集的大小不变，但可能需要对结果进行逆变换才能解释数据。变换也可能会使数据的解释变得更复杂，因此需要根据具体情况进行选择。
2.2 多维数据分析
2.2.1 主成分分析（PCA）
主成分分析（PCA）是一种常用的数据降维技术，它通过线性变换将多个变量转换成少数几个主成分，这些主成分可以捕捉数据集中的大部分变异性。在MATLAB中，可以利用pca函数来实现PCA分析。
% 假设C是一个含有多个变量的数据集[C_scores, C_loadings] = pca(C);登录后复制
在上述代码中，C_scores是主成分得分矩阵，它表示每个观测值在新的主成分空间中的位置；C_loadings是载荷矩阵，它表示原始变量在主成分上的权重。
使用PCA进行数据降维
降维是PCA最常见的用途之一，通过减少数据的维度，我们可以去除冗余信息，同时保留数据的主要结构。这对于可视化和后续的统计分析都非常有用。
% 绘制解释的方差百分比figure;pareto(C_loadings(:,1:3).^2);title('方差百分比');xlabel('主成分');ylabel('解释的方差百分比');登录后复制
在上述示例中，我们使用pareto函数绘制了前三个主成分解释的方差百分比，这有助于我们选择合适的主成分数量。
2.2.2 聚类分析技术
聚类分析是一种将数据集中的样本划分为若干组（类）的技术，使得同一类中的样本之间相似度较高，而不同类的样本相似度较低。MATLAB提供了多种聚类分析工具，包括K-means、层次聚类和DBSCAN等。
K-means聚类
K-means是一种最常用的聚类方法，它通过迭代计算类中心点并将样本分配给最近的类中心点，从而达到聚类的目的。在MATLAB中，可以使用kmeans函数来执行K-means聚类：
% 假设D是一个数据集[idx, C] = kmeans(D, 3);登录后复制
在此代码中，idx是每个数据点所属的类别的索引，C是每个类别的中心点。kmeans函数的第二个参数指定了聚类的数量，在此例中为3。
层次聚类
层次聚类是一种不同的聚类方法，它通过逐步合并或分割数据集中的子集来构建一个聚类树（或称为树状图）。这种方法能够得到一个聚类的层次结构，从而在不同层级上分析数据集的聚类特征。
Z = linkage(D, 'average');登录后复制
上述代码中的linkage函数用于计算层次聚类的树状图，'average'参数表示使用类平均法来计算类间的距离。该函数返回一个聚类的树状结构Z，随后可以使用dendrogram函数来绘制树状图。
2.3 高级数据可视化
2.3.1 热图和箱线图的绘制
MATLAB提供了一系列丰富的工具来进行高级数据可视化，这对于理解数据的分布和特性非常有帮助。热图和箱线图是两种常用的可视化手段，它们能直观地展示数据的统计特性。
热图绘制
热图是一种通过颜色变化来表示数据值大小的图表。在MATLAB中，可以使用heatmap函数来绘制热图：
% 假设E是一个数据矩阵figure;heatmap(E);登录后复制
heatmap函数能够自动选择一个颜色映射，以突出数据矩阵中的模式。通过调整其参数，还可以自定义颜色映射、行列标签以及其他视觉样式。
箱线图绘制
箱线图可以展示数据的分布，包括中位数、四分位数以及可能的异常值。在MATLAB中，可以使用boxplot函数来绘制箱线图：
% 假设F是一个数据集figure;boxplot(F);登录后复制
boxplot函数为每个数据集绘制了一个箱线图，能够清晰地显示数据的分布情况。此外，它还提供了调整箱线图样式的参数，使得图表更加符合用户的需求。
2.3.2 交互式数据可视化工具
除了基本的绘图函数，MATLAB还提供了交互式的数据可视化工具，这使得用户能够更灵活地探索和展示数据。其中，uifigure和uicontrol提供了创建自定义用户界面的功能，这些界面可以包含图形对象、按钮、滑块等多种交互元素。
创建交互式图表
为了创建一个交互式图表，我们通常需要使用uifigure创建一个图形界面，并在其中添加uitable、uicontrol等控件来构建交互元素。
% 创建一个交互式图形界面fig = uifigure('Name', '交互式热图');uicontrol(fig, 'Style', 'pushbutton', 'String', '绘制热图', 'Position', [20, 20, 100, 30], 'Callback', @plotHeatMap);% 热图绘制的回调函数function plotHeatMap(src, event) % 假设数据已经准备好 data = rand(10,10); % 随机数据用于示例 heatmap(data);end登录后复制
在上述示例中，我们创建了一个按钮，当用户点击按钮时，会触发plotHeatMap函数，从而绘制热图。这种交互式图形界面允许用户动态地与数据进行交互，从而更深入地理解数据。
通过这些高级可视化技术，数据科学家和研究人员能够更有效地探索和传达数据的特性，从而作出更加明智的数据驱动决策。
3. 生物统计模型构建与优化
3.1 统计模型的选择与构建
在生物统计领域，构建适当的统计模型是分析和解释数据的关键步骤。选择何种统计模型依赖于研究的具体需求和数据的特性。接下来，我们将重点讨论两种常见的统计模型——线性回归与逻辑回归，以及生存分析模型，并介绍它们在生物统计中的应用。
3.1.1 线性回归与逻辑回归
线性回归是应用最广泛的统计模型之一，适用于研究两个或多个变量之间的线性关系。在生物统计中，线性回归常用于解释一个连续因变量和一个或多个自变量之间的关系。线性回归模型的一般形式是：
Y = β0 + β1X1 + β2X2 + ... + βnXn + ε登录后复制
其中，Y 是因变量，X1 到 Xn 是自变量，β0 是截距项，β1 到 βn 是各自变量的系数，而 ε 是误差项。
逻辑回归是线性回归的扩展，用于因变量为二分类的情况。它的模型形式如下：
logit(P) = ln[P/(1-P)] = β0 + β1X1 + β2X2 + ... + βnXn登录后复制
其中，P 是事件发生的概率，logit 函数是逻辑回归的核心，β0 到 βn 同线性回归。
在MATLAB中，我们使用 fitlm 函数来执行线性回归分析，而逻辑回归可以使用 fitglm 函数，并指定模型为二项分布。
% 线性回归lm = fitlm(X, Y);% 逻辑回归glm = fitglm(X, Y, 'Distribution', 'binomial');登录后复制
3.1.2 生存分析模型
生存分析是生物统计中的一个重要领域，用于处理和分析生存时间数据，即从研究开始到某个事件（如死亡或复发）发生之间的时间。最常用的生存分析模型是Cox比例风险模型。Cox模型的基本形式如下：
h(t|X) = h0(t)exp(β1X1 + β2X2 + ... + βnXn)登录后复制
这里，h(t|X) 是风险函数，h0(t) 是基线风险函数，β1 到 βn 是回归系数，X1 到 Xn 是协变量。
在MATLAB中，我们可以使用 fitcox 函数来拟合Cox比例风险模型：
% Cox回归模型coxModel = fitcox(X, Y);登录后复制
3.2 模型评估与验证
模型构建后，需要评估其有效性，并通过验证来确保模型能够准确地预测或解释数据。本节将介绍模型交叉验证方法以及ROC曲线和AUC值分析这两种主要的模型评估技术。
3.2.1 模型的交叉验证方法
交叉验证是一种评估模型泛化能力的技术，可以减少模型评估的方差，提高对新数据的预测能力。在交叉验证中，数据集被分成 k 个大小大致相同的子集。模型在 k-1 个子集上进行训练，然后在剩余的一个子集上进行测试。这个过程重复 k 次，每次使用不同的测试集，最后将 k 次的结果进行汇总以评估模型性能。
在MATLAB中，我们可以使用 crossval 函数进行k折交叉验证：
% 假设 model 是已拟合的回归模型k = 5; % 选择5折交叉验证cvModel = crossval(model, 'KFold', k);cvLoss = kfoldLoss(cvModel);登录后复制
3.2.2 ROC曲线与AUC值分析
ROC曲线（接收者操作特征曲线）和AUC值（曲线下面积）是评估分类模型性能的常用方法。ROC曲线以假正率（FPR）为x轴，真正率（TPR）为y轴绘制，并且AUC值越接近1，表示模型的分类性能越好。
在MATLAB中，我们可以使用 perfcurve 函数来绘制ROC曲线并计算AUC值：
% 假设 YPredicted 是预测的二分类概率，YActual 是实际的标签（0或1）[fpr, tpr, thresholds] = perfcurve(YActual, YPredicted, 1);aucValue = trapz(fpr, tpr); % 计算AUC值% 绘制ROC曲线plot(fpr, tpr);xlabel('False Positive Rate');ylabel('True Positive Rate');title('ROC Curve');登录后复制
ROC曲线可以直观地展示模型在不同阈值下的性能，并且帮助我们选择一个适当的决策阈值。
3.3 高级统计分析技术
随着统计学的发展，研究者开发了更多的统计技术来处理复杂的数据分析问题。本节将介绍方差分析（ANOVA）和协方差分析，以及时间序列分析这两种高级统计分析技术。
3.3.1 方差分析（ANOVA）与协方差分析
方差分析（ANOVA）用于检验三个或以上组别间的均值是否存在显著差异。ANOVA的基本思想是将总的变异分为组内变异和组间变异，并计算它们的比例。如果组间变异相对于组内变异显著，那么就可以认为不同组别间的均值存在显著差异。
协方差分析（ANCOVA）是ANOVA的扩展，它在模型中加入了协变量，这些协变量可以是连续的，用于控制额外变量对响应变量的影响。
在MATLAB中，我们可以使用 anova1 函数来执行单因素方差分析：
% 单因素方差分析pValue = anova1(X, Y);登录后复制
而 manova 函数可以用来执行多因素方差分析：
% 多因素方差分析pValue = manova([X1, X2], Y);登录后复制
3.3.2 时间序列分析
时间序列分析用于分析按时间顺序排列的数据点，以预测未来的数据值或识别其中的模式。在生物统计学中，时间序列分析可以应用于研究基因表达随时间的变化等。
时间序列分析涉及到平稳性检验、自回归移动平均（ARMA）模型、差分等概念。平稳性是指时间序列的统计特性不随时间改变的性质。ARMA模型是时间序列分析中一个重要的建模方法，它可以将时间序列分解为自回归部分和移动平均部分。
MATLAB提供了多个工具箱，如Econometrics Toolbox，其中包含用于时间序列分析的函数，例如 arima 函数，用于创建ARMA模型：
model = arima('Constant', 0, 'D', 1, 'Seasonality', 12, 'MALags', 1:3, 'SMALags', 1:3);登录后复制
本章节深入探讨了统计模型的构建与优化过程。从选择和构建不同类型的统计模型，到运用交叉验证和ROC-AUC分析对模型进行评估，再到掌握更复杂的方差分析和时间序列分析技术，这些知识构成了生物统计学中的核心部分。在实际应用中，这些技术帮助研究者更好地理解数据，以及更准确地预测和解释生物学中的现象。随着技术的不断进步，生物统计学家现在可以利用这些强大的统计方法来处理以前难以克服的复杂问题。
4. 生物信息学中的应用实例
4.1 基因表达数据分析
4.1.1 微阵列数据处理
微阵列技术是生物信息学中用于研究基因表达水平的常用工具。它能够同时监测成千上万的基因表达情况，但数据分析过程需要经过一系列复杂步骤来保证结果的准确性。在MATLAB中，我们可以利用Bioinformatics Toolbox来处理这些数据。
MATLAB中处理微阵列数据的步骤大致包括：数据预处理、归一化、差异表达分析、功能注释和富集分析。
首先，进行数据预处理，包括去除或填补缺失值、过滤噪声信号。以数据填补为例，MATLAB提供impute函数，能够实现这一功能。处理后，通常需要将数据归一化，以消除批次效应或技术变异，常用的方法有Z分数法、LOWESS法等。
% 假设微阵列数据存储在变量 microarrayData 中normalizedData = normalize(microarrayData, 'method', 'zscore');% 使用箱线图查看归一化效果boxplot(normalizedData);登录后复制
数据归一化后，接下来进行差异表达分析，确定哪些基因在实验条件之间存在显著的表达差异。常用的统计测试包括t检验和ANOVA。MATLAB的ttest或anova函数可用于此目的。例如，对于两组数据的比较：
% 假设条件1和条件2的数据分别在变量condition1和condition2中[h, pValue] = ttest(condition1, condition2);% 根据p值判断是否差异显著significantGenes = pValue < 0.05;登录后复制
差异表达基因确定后，可以进行功能注释和富集分析，以了解这些基因在生物过程中的角色。MATLAB中可以利用goana和kegga函数来进行这些分析：
% 进行基因本体（GO）富集分析GO_results = goana(diffExpGenes, geneAnnotation);% 进行KEGG通路富集分析KEGG_results = kegga(diffExpGenes, geneAnnotation);登录后复制
MATLAB的Bioinformatics Toolbox为基因表达数据的处理提供了丰富的函数，便于用户进行复杂的数据分析。
4.1.2 转录组数据分析
转录组学是研究一个细胞或组织中所有RNA分子的集合，尤其是mRNA。与微阵列数据类似，转录组数据也需通过一系列分析步骤，以识别和解释在不同条件下基因表达的变化。
在MATLAB中，转录组数据处理的典型流程如下：

高通量测序数据的质量控制和预处理。
序列比对，将测序得到的短读段（reads）映射到参考基因组。
基因表达量的定量。
差异表达基因的识别。
基因表达模式和生物功能的分析。

以质量控制为例，MATLAB支持FASTQ格式的文件读取与处理。可以使用fastqinfo和fastqread函数来获取序列质量信息并读取序列数据。之后，借助Bioinformatics Toolbox中的fastqfprintf函数，可以对质量分数进行可视化。
% 读取FASTQ文件信息info = fastqinfo('sample.fastq');% 读取FASTQ文件中的序列reads = fastqread('sample.fastq');% 质量分数可视化fastqfprintf('sample.fastq', info.MinQuality:info.MaxQuality);登录后复制
接下来，进行序列比对，将读段映射到参考基因组，可以使用MATLAB的bowtiebuild和bowtie函数，或者bwa函数来构建索引和进行比对。
% 构建参考基因组的Bowtie索引bowtiebuild(info.Reference, 'genome');% 比对读段到参考基因组samFile = 'alignments.sam';[status, msg] = bowtie(info.Reference, 'reads.fastq', samFile);登录后复制
通过上述步骤，得到了比对后数据，可以使用featurecount函数进行基因表达量的定量，然后利用edgeR或DESeq2等包进行差异表达基因的分析，这些在MATLAB环境中也可实现，或通过接口与R语言环境交互。
最后，我们使用pathwayAnalysis函数进行富集分析，探索差异表达基因参与的生物过程或通路。
% 差异表达基因和背景基因列表diffExpGenes = find(diffExpGenes);backgroundGenes = find(backgroundGenes);% KEGG通路富集分析[keggTable, keggFigure] = pathwayAnalysis(diffExpGenes, backgroundGenes);登录后复制
以上是转录组数据分析在MATLAB中的一些基本步骤，而在实际应用中，可能需要对不同的数据分析工具与方法进行对比，选取最适合当前数据集和研究目的的策略。
5. MATLAB生物统计的进阶拓展
5.1 集成其他编程语言
随着跨学科研究的不断深入，MATLAB与其他编程语言如R和Python的集成变得越来越重要。通过集成，我们可以利用各自语言的优势，解决更复杂的问题。
5.1.1 MATLAB与R语言的交互
MATLAB提供了与R语言交互的接口，允许用户在MATLAB环境中调用R语言编写的函数，反之亦然。R语言在统计分析领域拥有大量的包，而MATLAB则在矩阵计算、工程领域有着深厚的积累。两者交互可以使我们充分利用两种语言的优势。
例如，在MATLAB中，我们可以使用以下命令来调用R语言的函数：
Rcmd = 'Rscript -e "r_function_name()}"';[status,cmdout] = system(Rcmd);登录后复制
这里的 "r_function_name()" 是R语言中定义的函数。通过这种方式，MATLAB用户可以直接在R环境中运行R函数，并获取输出结果。
5.1.2 MATLAB与Python的数据交换
Python作为一门流行的语言，也经常被用于数据科学和生物信息学领域。MATLAB与Python的集成允许用户从MATLAB中调用Python脚本，或者在Python中调用MATLAB函数。
在MATLAB中使用Python，我们可以借助py对象，它允许Python代码在MATLAB中作为对象进行操作：
import pythonpy.xlabel('x')py.ylabel('y')py.title('Plot title')py.plot(py.numpy.array([1, 2, 3]), py.numpy.array([4, 5, 6]))登录后复制
上述代码演示了如何在MATLAB中创建一个简单的Python绘图，这展示了MATLAB和Python的完美结合。
5.2 生物统计软件包的开发
MATLAB在开发专业的生物统计软件包方面具有独特优势，这些软件包可以用来封装复杂的算法并创建易用的用户界面。
5.2.1 自定义函数与工具箱的创建
在MATLAB中创建自定义函数和工具箱，可以通过函数编写、文件组织以及提供文档的方式进行。这可以帮助我们简化重复的工作，提高工作效率。
下面是一个简单的自定义函数示例：
function y = myCustomFunction(x) % 这是一个简单的示例函数，进行简单的数学运算 y = x^2 + 2*x + 1;end登录后复制
创建自定义函数后，可以将这些函数组织到一个工具箱中，为不同的生物统计应用提供服务。
5.2.2 算法封装与用户界面设计
为了使非专业用户也能方便地使用复杂的生物统计分析工具，MATLAB提供了GUI设计功能。例如，使用GUIDE或App Designer工具可以快速创建用户友好的图形用户界面。
以App Designer为例，可以拖放控件来设计界面，并将用户界面动作绑定到特定的回调函数，如下所示：
% Callback function of a push buttonfunction pushButtonPushed(app, event) data = app.dataEditField.Value; result = myCustomFunction(data); app.resultLabel.Text = ['Result: ', num2str(result)];end登录后复制
这段代码演示了如何将一个按钮点击事件与自定义函数关联起来，并更新GUI上的结果显示。
5.3 人工智能在生物统计中的应用
人工智能（AI）技术正在变革生物统计和生物医学领域。MATLAB提供了强大的AI工具，特别是机器学习和深度学习。
5.3.1 机器学习技术概述
机器学习是AI的一个分支，它让计算机系统能够从数据中学习并改进性能，而无需明确编程。MATLAB通过其统计和机器学习工具箱提供了广泛的机器学习算法。
一些常见的机器学习技术包括：

线性回归
决策树
支持向量机（SVM）
随机森林
聚类分析等

5.3.2 MATLAB在生物医学领域的深度学习应用案例
MATLAB提供了深度学习工具箱，这使得研究人员能够设计、训练和部署深度神经网络进行各种生物医学任务，如图像识别、序列预测等。
下面是一个简单的深度学习示例，展示了如何构建并训练一个用于分类的神经网络：
layers = [ imageInputLayer([28 28 1]) convolution2dLayer(5, 20) reluLayer maxPooling2dLayer(2, 'Stride',2) fullyConnectedLayer(10) softmaxLayer classificationLayer];% 加载数据digitDatasetPath = fullfile(matlabroot, 'toolbox', 'nnet', 'nndemos',... 'nndatasets', 'DigitDataset');digitData = imageDatastore(digitDatasetPath,... 'IncludeSubfolders',true,'LabelSource','foldernames');% 分割数据集为训练和测试集[trainingImages,validationImages] = splitEachLabel(digitData,0.8,'randomize');% 训练神经网络options = trainingOptions('sgdm',... 'MaxEpochs',15,... 'InitialLearnRate',0.01,... 'Verbose',false,... 'Plots','training-progress');net = trainNetwork(trainingImages,layers,options);% 测试神经网络predictedLabels = classify(net,validationImages);accuracy = sum(predictedLabels == validationImages.Labels)/numel(validationImages.Labels);登录后复制
在这个案例中，我们使用了一个简单的卷积神经网络来识别手写数字。此代码展示了数据加载、模型构建、训练和预测的整个流程。
通过以上内容，我们可以看到MATLAB在生物统计领域的进阶拓展方面的强大功能和灵活性。无论是集成其他编程语言、开发专业软件包，还是应用人工智能技术，MATLAB都提供了丰富的工具和方法。这使得生物统计学家和相关领域的研究人员能够以更高的效率和更深入的洞察力进行研究和创新。