MATLAB生物统计实战手册：从数据处理到报告输出一步到位

# 1. MATLAB在生物统计中的应用概述

## 1.1 MATLAB简介
MATLAB是一种高性能的数值计算环境和第四代编程语言，它广泛应用于工程、生物科学、经济学、数学等领域。在生物统计中，MATLAB提供了一系列工具箱，可以有效地进行数据分析、算法开发以及复杂统计模型的创建和测试。

## 1.2 MATLAB在生物统计中的作用
生物统计学是应用统计学原理和方法研究生物科学问题的学科。MATLAB能够提供强大的数学计算、数据可视化和统计分析功能，这使得MATLAB在生物统计领域有着广泛的应用前景。例如，MATLAB可以用于基因表达数据分析、生物信息学研究、系统生物学模拟等。

## 1.3 MATLAB与其他统计软件的比较
相较于其他统计软件，MATLAB的优势在于其高度集成化和强大的矩阵计算能力，以及丰富的函数和工具箱支持。MATLAB的图形用户界面(GUI)使得操作更为简便直观，且其编程环境对于高级用户来说更易于自定义复杂的统计分析过程。然而，对于专注于统计分析的软件，如R或SAS，MATLAB在某些特定统计方法和算法的实现上可能稍显不足，因此选择合适的工具需要根据具体项目需求来定。

# 2. MATLAB数据处理基础

## 2.1 数据输入与输出技巧

### 2.1.1 导入生物数据到MATLAB

在生物统计分析中，数据的导入是开始工作前的首要步骤。MATLAB提供了多种方法来导入数据，包括使用MATLAB的数据导入工具和编写脚本来自动导入数据。生物数据通常以CSV、Excel、文本文件或专业软件导出的格式存在。

以下示例代码展示了如何使用MATLAB命令将CSV格式的生物数据导入到MATLAB环境：

% 假设CSV文件名为 'biostat_data.csv'
filename = 'biostat_data.csv';
data = readtable(filename, 'ReadVariableNames', true);

% 显示导入的数据
disp(data);

该代码中的 `readtable` 函数会读取CSV文件，并将数据以表格形式存储。参数 `'ReadVariableNames', true` 确保第一行将被用作列名。`disp` 函数用于在MATLAB命令窗口中显示表格数据。

### 2.1.2 数据的导出和存储

在MATLAB中处理完数据之后，我们通常需要将其导出到其他格式的文件中，比如CSV、Excel或二进制文件，以便于后续分析或与他人分享。以下是一个将数据导出为CSV文件的示例：

% 假设变量 'processedData' 包含处理后的数据
processedData = data; % 这里是处理后的数据集
outputFilename = 'processed_biostat_data.csv';

% 将数据导出为CSV文件
writetable(processedData, outputFilename, 'FileType', 'csv');

% 检查文件是否成功创建
if exist(outputFilename, 'file')
    disp(['数据已成功导出至文件: ', outputFilename]);
else
    disp('数据导出失败！');
end

在这段代码中，`writetable` 函数用于将表格数据导出为CSV文件。'FileType' 参数指定了文件类型。最后使用 `exist` 函数来验证文件是否已成功创建。

## 2.2 数据预处理和清洗

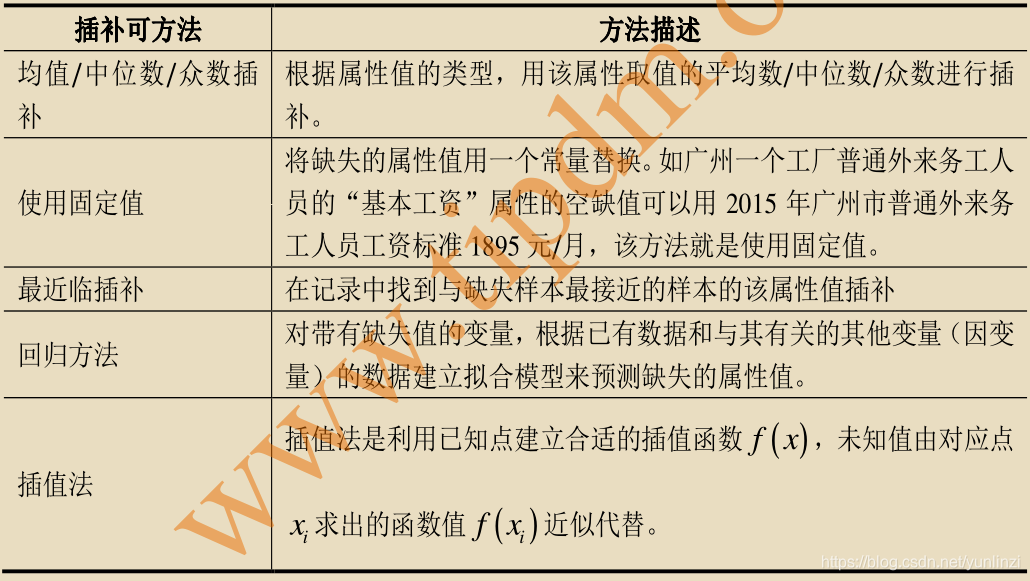
### 2.2.1 缺失值的处理

生物统计数据常常包含缺失值，这会对后续的分析产生影响。处理缺失值的方法有多种，常见的包括删除含有缺失值的记录、用平均值、中位数或众数填充缺失值。

以下是一个用平均值填充缺失值的示例：

% 假设 'biostat_data' 包含原始数据，数据类型为表格
biostat_data = readtable('biostat_data.csv', 'ReadVariableNames', true);

% 计算每列的平均值，忽略NaN值
colMeans = mean(biostat_data, [], 'omitnan');

% 填充缺失值
biostat_data_filled = varfun(@(x) ifelse(isnan(x), colMeans(size(biostat_data,2)), x), biostat_data);

% 显示处理后的数据
disp(biostat_data_filled);

这里使用了 `mean` 函数计算每列的平均值，并使用 `varfun` 和匿名函数对数据集中的缺失值进行了替换处理。

### 2.2.2 异常值的检测与处理

异常值是那些与数据集中的其他观测值显著不同的值。检测异常值可以使用统计规则，比如Z得分、IQR(四分位距)等。一旦发现异常值，我们可以决定将其删除或进行修正。

以下是一个使用Z得分检测异常值的示例代码：

% 假设 'biostat_data' 包含已填充缺失值的数据
z_scores = zscore(biostat_data{:,:}); % 计算Z得分

% 定义一个阈值
threshold = 3;

% 找出异常值
outliers = find(abs(z_scores) > threshold);

% 显示异常值
disp('异常值位于：');
disp(outliers);

这里，`zscore` 函数计算了数据集的Z得分。异常值是通过比较阈值来确定的。找出异常值后，您可以根据需要进行进一步的处理。

### 2.2.3 数据标准化和归一化

标准化和归一化是常见的数据预处理步骤，目的在于使数据具有相同的尺度或范围，从而避免某些算法因变量尺度不同而产生偏差。

以下是一个标准化处理的示例代码：

% 假设 'biostat_data' 包含已处理缺失值和异常值的数据
standardized_data = zscore(biostat_data{:,:}); % 标准化数据

% 创建标准化数据表格
standardized_table = array2table(standardized_data, 'VariableNames', biostat_data.Properties.VariableNames);

% 显示标准化后的数据
disp('标准化后的数据：');
disp(standardized_table);

在这段代码中，`zscore` 函数用来标准化数据，将数据集中的每一列按其均值中心化并缩放为单位方差。结果被重新组织成表格格式，以便于查看和进一步的分析。

## 2.3 数据可视化基础

### 2.3.1 绘制基本统计图表

数据可视化是数据分析中不可或缺的一部分，可以帮助研究者直观地理解数据。MATLAB提供了多种绘图功能，如直方图、散点图和箱形图等。

以下是如何使用MATLAB绘制直方图的示例：

% 假设 'dataVariable' 是我们感兴趣的变量名
dataVariable = biostat_data.dataVariable;

% 绘制直方图
figure;
histogram(dataVariable);
title('变量的直方图');
xlabel('值');
ylabel('频率');

这里，`histogram` 函数用于生成直方图，`figure` 创建了一个新的图形窗口，标题和坐标轴标签则用以描述图表内容。

### 2.3.2 高级数据可视化技术

随着数据分析的深入，我们可能会用到更高级的可视化技术，例如叠加不同数据集的图形、三维散点图或热图等。

下面是一个使用热图显示两个变量相关性的示例：

% 假设 'dataVariable1' 和 'dataVariable2' 是两个相关变量
dataVariable1 = biostat_data.dataVariable1;
dataVariable2 = biostat_data.dataVariable2;

% 创建热图矩阵
heatmap(dataVariable1, dataVariable2);

% 添加标题和轴标签
title('变量1和变量2的相关性热图');
xlabel('变量1');
ylabel('变量2');

在这段代码中，`heatmap` 函数用来创建表示两个变量相关性的热图。这样的可视化可以帮助理解变量之间的关系。

总结而言，在本章节中，我们详细探讨了数据输入输出、预处理及清洗、可视化等关键步骤。理解并掌握这些基础知识对于有效开展生物统计分析至关重要。下一部分我们将深入到生物统计分析的方法中，为处理复杂数据集和建立统计模型打下坚实的基础。

# 3. 生物统计分析方法

在第二章中，我们已经讨论了MATLAB在生物统计中的数据处理基础，为进行深入的生物统计分析打下了坚实的基础。第三章将介绍一些常见的生物统计分析方法，包括描述性统计分析、假设检验与方差分析以及相关性和回归分析。

## 3.1 描述性统计分析

描述性统计分析是统计学中用来总结和描述数据特征的方法。通过对数据集进行汇总，我们可以得到数据的基本统计量，如均值、中位数、众数、标准差等。这有助于我们对数据有一个初步的了解，并为后续的复杂分析提供基础。

### 3.1.1 常用描述性统计量的计算

在MATLAB中计算描述性统计量非常简单。例如，给定一个生物数据集，我们可以使用以下代码来计算基本的统计量：

data = [1.2, 2.4, 3.5, 4.1, 5.0]; % 示例数据集
mean_value = mean(data); % 计算均值
median_value = median(data); % 计算中位数
mode_value = mode(data); % 计算众数
std_dev = std(data); % 计算标准差

fprintf('均值: %.2f\n', mean_value);
fprintf('中位数: %.2f\n', median_value);
fprintf('众数: %.2f\n', mode_value);
fprintf('标准差: %.2f\n', std_dev);

在上述代码中，`mean()`, `median()`, `mode()`, 和 `std()` 函数分别用于计算均值、中位数、众数和标准差。结果会通过 `fprintf` 函数输出到MATLAB的命令窗口中。

### 3.1.2 分布的可视化展示

除了计算描述性统计量，我们还经常需要可视化数据的分布情况，以直观地理解数据特征。MATLAB提供了多种函数来绘制不同类型的统计图表。例如，我们可以通过绘制直方图来展示数据分布：

histogram(data); % 绘制直方图
title('数据集直方图');
xlabel('数值');
ylabel('频率');

这段代码将生成一个直方图，直方图是将数据范围分段并计算每段中数据点的数量，然后以柱状图的形式展现出来。通过直方图，我们可以直观地看到数据的分布情况，是否存在偏态，以及数据的分散程度。

## 3.2 假设检验与方差分析

在生物统计学中，假设检验用来确定实验结果是否具有统计学意义，而方差分析（ANOVA）是用来检验三个或更多样本均值之间是否存在显著差异的方法。

### 3.2.1 常见假设检验方法

MATLAB提供了多种函数来执行不同的假设检验，包括 t 检验、卡方检验、F 检验等。例如，对于一个两样本均值的比较，我们可以使用 t 检验：

sample1 = [1.2, 2.4, 3.5, 4.1, 5.0];
sample2 = [2.1, 3.2, 4.3, 5.4, 6.5];

[h, p, ci, stats] = ttest2(sample1, sample2); % 执行两样本 t 检验

fprintf('p 值: %.3f\n', p);
if h == 1
    fprintf('在显著性水平 %.0f%% 下，拒绝零假设，认为两样本均值有显著差异。\n', 100 * (1 - stats.significance_level));
else
    fprintf('在显著性水平 %.0f%% 下，不能拒绝零假设，认为两样本均值无显著差异。\n', 100 * (1 - stats.significance_level));
end

在这段代码中，`ttest2()` 函数用于执行两个独立样本的 t 检验，`h` 是假设检验的结果，`p` 是 p 值，`ci` 是置信区间，`stats` 是检验统计量的详细信息。我们根据 p 值与显著性水平来决定是否拒绝零假设。

### 3.2.2 方差分析（ANOVA）原理与实践

方差分析是对两个以上样本均值进行比较的统计方法。在MATLAB中，可以使用 `anova1` 函数来进行单因素方差分析：

group1 = [1.2, 2.4, 3.5];
group2 = [2.1, 3.2, 4.3];
group3 = [3.1, 4.2, 5.3];

p = anova1([group1; group2; group3]); % 执行单因素方差分析

fprintf('p 值: %.3f\n', p);
if p < 0.05
    fprintf('至少有一个组的均值与其他组存在显著差异。\n');
else
    fprintf('没有足够的证据表明各组均值存在显著差异。\n');
end

在这段代码中，`anova1` 函数用于进行单因素方差分析。结果的 p 值小于0.05表示至少有一组的均值与其他组的均值存在显著差异。

## 3.3 相关性和回归分析

相关性和回归分析是研究变量之间关系的重要工具。相关系数可以衡量变量之间的线性关系程度，而回归分析可以帮助我们建立一个或多个自变量和因变量之间的关系模型。

### 3.3.1 相关系数的计算和意义

在MATLAB中计算相关系数可以使用 `corrcoef` 函数：

x = [1, 2, 3, 4, 5];
y = [5, 4, 2, 3, 1];

[r, p] = corrcoef(x, y); % 计算相关系数

fprintf('相关系数: %.2f\n', r);
if p < 0.05
    fprintf('在显著性水平0.05下，x 和 y 存在显著相关关系。\n');
else
    fprintf('在显著性水平0.05下，x 和 y 不存在显著相关关系。\n');
end

在这段代码中，`corrcoef` 函数计算了 x 和 y 的相关系数 `r` 以及相关性的显著性检验 p 值 `p`。相关系数的值介于 -1 和 1 之间，接近 1 或 -1 表示强正相关或强负相关。

### 3.3.2 线性回归模型的建立和评估

线性回归分析是生物统计中常见的回归分析方法，用于研究自变量和因变量之间的线性关系。在MATLAB中，可以通过 `fitlm` 函数来建立线性回归模型：

x = [1, 2, 3, 4, 5];
y = [5, 4, 2, 3, 1];

lm = fitlm(x, y); % 建立线性回归模型

fprintf('回归方程: y = %.2fx + %.2f\n', lm.Coefficients.Estimate(1), lm.Coefficients.Estimate(2));
fprintf('R-squared: %.2f\n', lm.Rsquared.Ordinary);

在这段代码中，`fitlm` 函数返回一个线性模型对象 `lm`，我们可以通过该对象获取回归系数和拟合优度（R-squared）。R-squared 的值越接近 1，表示模型对数据的解释能力越强。

在进行线性回归分析时，评估模型的拟合优度和检验回归系数的显著性是非常重要的。这有助于我们理解模型是否真正揭示了自变量和因变量之间的关系。

在本章中，我们详细介绍了描述性统计分析、假设检验与方差分析以及相关性和回归分析的原理和实践。这些方法是生物统计分析的核心内容，有助于研究者深入理解数据特征和变量间的关系。通过MATLAB的应用，我们可以高效地进行计算和可视化分析，为生物统计研究提供有力的支持。在下一章中，我们将探索更高级的生物统计功能，包括时间序列分析、高维数据分析以及生存分析和风险评估。

# 4. ```
# 第四章：高级生物统计功能实现

生物统计学领域不断进步，对统计方法的要求也越来越高。MATLAB作为强大的工程计算工具，在高级统计分析领域提供了丰富的功能和算法。在本章中，我们将探讨如何使用MATLAB实现时间序列分析、高维数据分析和生存分析等高级统计功能。

## 4.1 时间序列分析

### 4.1.1 时间序列数据的基本处理

时间序列数据是指按照时间顺序排列的数据点集合。在生物统计中，时间序列分析可以帮助我们研究和预测随时间变化的现象，例如疾病传播率的季节性波动、药物反应的动态过程等。

在MATLAB中，我们可以使用内置函数和工具箱来处理时间序列数据。首先，需要将数据导入MATLAB环境，并转换为时间序列对象。例如，假设我们有一个按月记录的病毒传播率数据集：

% 假设 date 和 rate 是两个向量，分别包含数据的时间点和对应的值
date = {'2021-01', '2021-02', '2021-03', ...}; % 时间点
rate = [1.2, 1.5, 1.7, ...]; % 相应的值
timeSeries = timeseries(rate, datenum(date, 'yyyy-mm')); % 创建时间序列对象

接下来，我们可以使用`detrend`函数去除趋势项，以获得平稳的时间序列：

detrendedSeries = detrend(timeSeries);

### 4.1.2 预测模型的构建与验证

为了预测未来趋势，可以使用ARIMA（自回归积分滑动平均）模型。MATLAB中的`arima`函数可以帮助我们建立模型：

model = arima('D',1,'Seasonality',12,'MALags',1); % 例如，季节性差分ARIMA模型
fitModel = estimate(model, detrendedSeries);

之后，我们可以使用建立的模型进行预测，并通过历史数据进行模型验证：

[forecastedValues, forecastedCI] = forecast(fitModel, 12, 'Y0', detrendedSeries);

其中，`forecastedValues`为预测值，`forecastedCI`为预测的置信区间。

## 4.2 高维数据分析

### 4.2.1 主成分分析（PCA）

在生物统计研究中，面对高维数据时，主成分分析（PCA）是一种常用的数据降维技术。PCA可以帮助我们识别数据中最重要的变异来源，减少数据维数，同时尽量保留原始数据的信息。

在MATLAB中，可以使用`pca`函数来进行PCA分析：

% 假设 X 是一个高维数据矩阵，每一行代表一个样本，每一列代表一个特征
[coeff, score, latent] = pca(X);

其中，`coeff`是主成分系数矩阵，`score`是转换后的数据点坐标（主成分得分），`latent`是每个主成分的方差解释量。

### 4.2.2 聚类分析

聚类分析是另一种高维数据分析方法，用于将相似的数据点分组在一起。MATLAB提供了`clusterdata`和`pdist2`等函数，用于实现聚类分析。

下面是一个简单的K均值聚类的例子：

% 假设 dataMatrix 是包含多个样本的数据矩阵
[idx, C] = kmeans(dataMatrix, 3); % 假设我们要将数据分为3类

其中，`idx`是每个样本所属类别的索引，`C`是聚类中心。

## 4.3 生存分析和风险评估

### 4.3.1 生存数据的探索和图形表示

生存分析是研究生存时间和生存状态的统计方法，在临床试验和流行病学研究中十分重要。MATLAB提供了一系列函数来进行生存分析。

首先，我们需要创建生存对象，并绘制生存曲线：

% 假设 time 是观测时间，status 是生存状态（0表示删失，1表示事件发生）
[survObj, time] = censor(time, status);
[survFit, survObj] = survfit(survObj);
plot(survFit);

### 4.3.2 Cox比例风险模型的实现

Cox比例风险模型是一种半参数生存分析模型，用于评估多个因素对生存时间的影响。在MATLAB中，我们可以使用`coxphfit`函数来拟合Cox模型：

% 假设 X 是协变量矩阵，riskTable 是风险表格，包含时间点和相应风险集信息
[beta, H, stats] = coxphfit(X, time, status, 'Baseline', riskTable);

其中，`beta`是估计的回归系数，`H`是基线累积风险函数，`stats`包含了统计信息，例如似然比检验的结果等。

通过上述分析，我们能够对不同特征对生存时间的影响进行定量评估。

在下一章，我们将深入探讨如何利用MATLAB实现生物统计报告的自动化，包括报告模板设计和动态数据图表的插入。

# 5. 生物统计报告自动化

## 5.1 利用MATLAB生成自动化报告

### 5.1.1 报告模板的设计

在现代研究中，自动化报告的生成已经成为提高效率的重要手段。MATLAB通过其内置的报告生成器，可以方便地创建包含动态内容的自动化报告。设计一个好的报告模板需要考虑以下几个关键要素：

- **布局和格式**：模板应该有一个清晰且一致的布局，以便于用户阅读。这包括文本、图片、图表和表格的排版。
- **内容的动态化**：报告中包含的数据和结果应该是动态的，即报告生成时能够自动更新为最新的分析结果。
- **交互性**：高级的报告可能会包含一些交互式的控件，允许用户在报告中改变参数或视角，得到不同的分析结果。
- **可重复使用性**：模板设计应尽可能通用，便于适应不同项目的需求，易于维护和更新。

为了设计一个报告模板，你首先需要确定报告的逻辑结构，然后使用MATLAB的Report Generator工具进行设计。下面给出一个简单的MATLAB代码示例，演示如何设置一个基本的报告模板：

% 创建报告对象
rpt = Report('ReportTemplate.rtf');

% 添加报告内容
rpt = add(rpt, 'Title', '我的生物统计报告');
rpt = add(rpt, 'Heading', '第一部分：描述性统计分析');
rpt = add(rpt, 'Paragraph', '以下是描述性统计分析的结果...');
rpt = add(rpt, 'Heading', '第二部分：假设检验结果');
rpt = add(rpt, 'Paragraph', '本部分展示了假没检验的相关结果...');

% 保存报告
save(rpt, '自动化报告.rtf');

以上代码展示了创建一个包含标题、段落、子标题等元素的基本报告结构，并将其保存为RTF文件。你可以将动态数据和图表插入到报告模板的指定位置。

### 5.1.2 报告中动态数据和图表的插入

在MATLAB中生成包含动态数据和图表的报告，可以使用MATLAB报告生成器中的特定函数。这些函数能够从分析脚本中提取数据，并将它们嵌入到报告中的适当位置。这一步骤的关键在于能够自动识别并填充报告模板中的占位符。

以下是一个插入动态数据和图表的示例：

% 假设我们已经完成了描述性统计分析并创建了一个表格
statsTable = describe(myData);

% 在报告中添加此表格
rpt = add(rpt, 'Table', statsTable, '格式化选项');

% 假设我们有一个用于描述性统计的图表
figure; % 创建一个新的图形窗口
histogram(myData);
title('数据直方图');

% 将图表保存为图片并插入到报告中
img = im2array(print('-dpng', gcf)); % 将当前图形保存为PNG格式图片
rpt = add(rpt, 'Image', img, '图片标题', '图片描述');

在上述代码中，我们使用`add`函数将描述性统计分析的结果表和直方图插入到报告中。`im2array`函数用于将图形转换为MATLAB可以操作的数组格式，然后被`add`函数插入到报告中相应的位置。

通过这样的方法，报告模板可以被填充以反映分析中的最新数据和结果，极大地简化了从数据分析到报告生成的过程。重要的是，当原始数据发生变化时，报告可以自动更新而无需人工干预。

## 5.2 报告结果的动态展示

### 5.2.1 交互式图形和控件的使用

MATLAB支持创建交互式的图形和控件，这使得报告的接收者可以在阅读报告时直接与内容进行交互。这种方法不仅提高了报告的可用性，还可以帮助用户更好地理解数据和结果。

在MATLAB中，你可以使用GUIDE或App Designer工具来设计包含控件的应用程序。以下是一个简单的例子，演示如何在报告中创建一个可交互的图表，允许用户选择不同的数据集进行展示：

% 创建一个新的图形窗口用于交互
fig = figure('Name', '交互式数据展示');

% 提供一些示例数据
dataSets = {'数据集1', '数据集2', '数据集3'};

% 添加一个下拉菜单控件
hPopup = uicontrol('Style', 'listbox', 'String', dataSets, ...
'Position', [100, 100, 200, 20], ...
'Callback', {@updatePlot, fig});

% 初始化绘制一个数据集的图表
data = rand(10, 1); % 假设数据
plot(data);
axis tight;

% 更新图表的回调函数
function updatePlot(src, ~, fig)
selectedData = src.Value;
data = eval(dataSets{selectedData});
plot(data);
axis tight;
end

在这个示例中，我们创建了一个带有下拉菜单的图形窗口，用户可以从中选择不同的数据集，并且每次选择都会触发一个回调函数来更新图表。这是一个交互式报告元素的典型例子，通过这种方式，报告变得更加动态且富有交互性。

### 5.2.2 结果的动态更新与分享

报告生成后，通常需要将其分享给团队成员或利益相关者。在生物统计学和数据分析领域，数据的实时更新意味着报告需要能够快速地反映出最新的分析结果。MATLAB通过其开发环境和集成的工具箱支持这一需求。

为了实现报告的动态更新与分享，可以采取以下步骤：

- **自动化报告生成脚本**：创建一个脚本，该脚本可以自动运行分析并生成最新的报告。将这个脚本配置为定时任务，可以确保报告定期更新。
- **集成报告生成至数据管道**：在你的数据处理和分析流程中，集成报告生成的步骤，确保在数据处理结束时自动触发报告生成。
- **使用Web应用分享报告**：借助MATLAB Web App Server，可以将生成的报告部署为Web应用，允许用户通过浏览器访问最新的报告内容。

下面是一个简单的示例，展示了如何使用MATLAB的定时任务功能来定期生成报告：

% 创建一个函数来生成报告
function generateReport()
% 运行数据分析
% ...

% 生成报告
% ...

% 保存报告到指定位置
saveReport(rpt, '报告路径\最新报告.rtf');
end

% 设置定时任务（仅作为概念展示）
scheduleTask('generateReport', 'daily', '09:00');

在上述示例中，`generateReport`函数负责分析数据和生成报告，并将其保存到指定的文件路径。然后使用`scheduleTask`函数将这个任务设置为每天上午9点执行，从而实现报告的自动更新。用户可以通过Web App Server访问最新版本的报告，无需担心手动更新的问题。

通过这些方法，你能够创建一个既动态又能及时反映最新数据的生物统计报告，极大地提高了报告的实用性和信息价值。

# 6. MATLAB生物统计案例分析

## 6.1 实际案例选择与数据描述

### 6.1.1 案例背景介绍

在这一小节中，我们将通过一个实际的生物统计案例来展示MATLAB的强大分析能力。案例将围绕一个生物信息学的问题展开，比如基因表达数据的分析。该案例将包括数据的导入、预处理、统计分析、模型构建以及最终结果的解释等步骤。

### 6.1.2 数据集的结构与内容

接下来，我们会详细描述用于案例分析的数据集结构和内容。以基因表达数据集为例，数据通常包括成百上千的基因表达水平，对应不同的生物样本和实验条件。数据集可能包含样本元数据，如样本类型、实验条件和时间点等信息。

## 6.2 案例分析流程演示

### 6.2.1 数据处理与分析步骤

本小节会介绍案例分析的具体步骤，包括数据导入、预处理、统计分析以及结果的初步解释。使用MATLAB的生物统计工具箱，可以方便地导入特定格式的数据（如CSV或者Excel文件），并进行数据清洗和预处理。

% 以导入CSV格式数据为例
data = readtable('gene_expression_data.csv');
% 进行数据预处理
dataClean = data(:,~ismember(names(data), {'Unnecessary', 'Columns'})); % 去除不需要的列
dataClean = rmmissing(dataClean); % 移除缺失值

### 6.2.2 结果的解释与报告撰写

在分析完数据后，会得到一系列统计量和图表。例如，可以得到基因表达差异的显著性分析结果，或者通过聚类分析揭示样本的潜在分组。这些结果需要用专业术语解释，并撰写成报告，报告中通常包括方法描述、结果展示和结论。

## 6.3 案例分析中的问题解决

### 6.3.1 遇到的常见问题及应对策略

在实际案例分析中，常常会遇到各种问题，比如数据的不完整性、异常值的干扰、模型过拟合等。针对这些问题，我们将讨论相应的解决策略。例如，使用不同的数据插补方法处理缺失值，或者运用稳健的统计方法应对异常值。

### 6.3.2 案例分析的经验总结

最后，我们会对整个案例分析进行经验总结，回顾分析流程中的关键步骤，并提炼出对类似分析有价值的见解和建议。这部分内容不仅对本案例有指导意义，还能够为类似研究提供参考。

% 一个简单的聚类分析示例
dataClustered = kmeans(dataClean, 3); % 假设我们想将数据分为3类
figure;
scatter3(dataClean(:,1), dataClean(:,2), dataClean(:,3), 36, dataClustered, 'filled');
title('基因表达数据聚类分析结果');
xlabel('表达水平1');
ylabel('表达水平2');
zlabel('表达水平3');

通过这样的案例分析，读者可以学习如何使用MATLAB进行生物统计问题的实际操作，以及如何解决过程中遇到的问题，最终将复杂的数据转化为有价值的分析结论。