基于并查集的集合交、并、差运算

# 1.1 并查集的概念

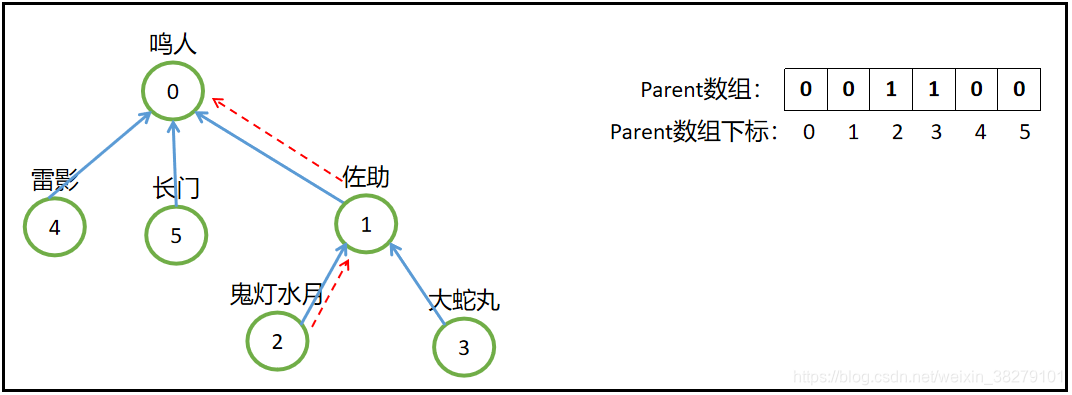
并查集（Disjoint Set）是一种用于处理集合合并与查询问题的数据结构。其主要目的是维护一个集合的划分，支持两种操作：查找元素所属的集合（Find）和合并两个集合（Union）。在并查集中，每个集合通常由一棵树表示，树的根节点代表该集合的标识元素，而每个非根节点指向其父节点，形成了一个树状结构。

通过路径压缩和按秩合并等优化方法，可以提高并查集的性能，使得查找和合并操作的时间复杂度近似为 O(1)。并查集广泛应用于各种算法和领域，如图论、最小生成树算法、连通性问题等。在实际应用中，可以利用并查集有效地处理集合操作，解决各种实际问题。

# 2. 并查集的基本操作

并查集（Disjoint Set）是一种常用的数据结构，常用来处理"动态连通性"相关问题。它主要支持以下几种基本操作：初始化并查集，查找根节点，合并两个集合的根节点。

### 2.1 初始化并查集

在初始化并查集时，每个节点都是一个单独的集合，且每个节点的父节点都指向自己，表示各自为一个独立的集合。

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]

### 2.2 查找根节点

查找根节点的过程就是不断向上遍历父节点，直到找到根节点，根节点的父节点指向自己，即 parent[i] == i。

def find(self, x):
    if self.parent[x] != x:
        self.parent[x] = self.find(self.parent[x])
    return self.parent[x]

### 2.3 合并两个集合的根节点

合并两个集合的根节点实际上就是将一个集合的根节点的父节点指向另一个集合的根节点，这样就实现了两个集合的合并。

def union(self, x, y):
    root_x = self.find(x)
    root_y = self.find(y)
    if root_x != root_y:
        self.parent[root_x] = root_y

现在我们已经了解了并查集的基本操作方法，包括初始化并查集、查找根节点以及合并两个集合的根节点。接下来我们将探讨并查集在集合运算中的实际应用。

# 3. 并、差运算的应用

在并查集中，除了基本