基于并查集的连通性问题求解

# 1. 并查集简介

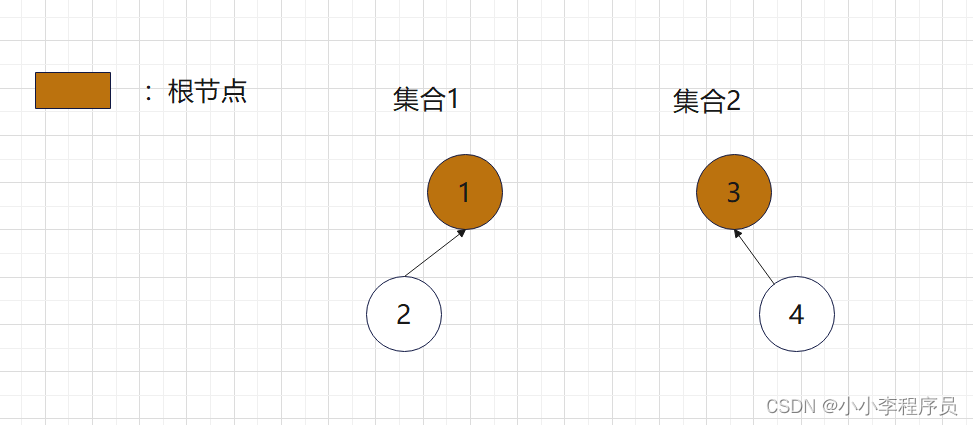
在计算机科学中，并查集是一种常见的数据结构，用于解决集合的合并与查询问题。它主要由查找和合并两个集合的操作组成，通常应用于连通性问题的求解。并查集的数据结构通常使用数组来表示，每个元素存储其父节点的索引，通过路径压缩和按秩合并等优化算法来提高效率。并查集在各种算法和数据结构中广泛应用，如最小生成树算法、图的连通性判断等。通过并查集，我们能够高效地处理集合的合并和查找操作，从而解决各类实际问题。在接下来的章节中，我们将深入探讨并查集的基本操作和在连通性问题中的应用。

# 2. 并查集的基本操作

#### 2.1 初始化并查集

在并查集的实现中，通常需要先初始化一些数据结构。一种常见的初始化方法是给每个节点赋予一个父节点指针，初始时父节点指针指向自身。这样可以通过查找父节点的方式来确定一个节点所在集合的根节点，方便后续的操作。下面是一个简单的初始化并查集的示例代码：

class UnionFind:
    def __init__(self, n):
        self.parent = [i for i in range(n)]

在这段代码中，我们通过初始化操作给每个节点都赋予了一个父节点指针，初始时指向自身。接下来我们将介绍如何通过路径压缩提高查找效率。

#### 2.2 查找根节点的路径压缩

在实际应用中，为了加速查找根节点的过程，我们可以通过路径压缩来优化。路径压缩的操作就是在查找父节点的同时，将沿途经过的所有节点直接连接到根节点上。这样可以减少之后查找操作的时间复杂度。下面是一个路径压缩的简单实现：

class UnionFind:
    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

在这段代码中，我们在查找根节点的同时进行路径压缩操作，将沿途经过的所有节点直接连接到根节点上，以减少查找的时间复杂度。下面我们将介绍如何合并两个集合并进行优化。

#### 2.3 合并两个集合的优化算法

除了查找操作的优化，合并操作也是并查集中需要考虑的优化点。一种常见的合并优化算法是按秩合并，即将秩较小的集合合并到秩较大的集合上。这样可以减少树的深度，提高后续操作的效率。下面是一个按秩合并的简单实现：

class UnionFind: