并查集的实现方法：数组存储

# 1. 引言

在计算机科学中，并查集是一种重要的数据结构，用于解决集合合并和查询问题。通过并查集，我们可以高效地判断两个元素是否属于同一个集合，并将不同的集合进行合并。在实际应用中，例如网络连通性判断、最小生成树算法和社交网络中的好友关系建立等方面，都可以看到并查集的身影。并查集的核心思想简单明了，但需要合理的数据结构和算法来实现。本文将介绍并查集的基本概念、树状结构、数组存储实现方法以及在不同领域的应用场景，希望能够帮助读者更深入地理解并查集的原理和应用。让我们一起来探索并查集的奥秘吧！

# 2. 基础概念

#### 树状结构

树状结构是一种非线性数据结构，由节点和边组成，其中有且仅有一个根节点，每个节点有零个或多个子节点。树的特点包括：根节点没有父节点，非根节点有且仅有一个父节点，任意节点之间形成唯一路径。

##### 树的定义与特点

树是一种层级结构，它的节点之间通过边（连接父节点和子节点的连线）相连。树的定义包括空树和非空树两种情况。非空树具有一个根节点，该节点没有父节点，其他节点都有且仅有一个父节点。树的特点之一是任意节点之间都有唯一的路径相连。

##### 树的遍历方式

树的遍历方式主要包括深度优先遍历（DFS）和广度优先遍历（BFS）。在深度优先遍历中，从根节点出发，沿着一个子树一直向下遍历，直到不能再继续深入，然后回溯到上一层节点继续遍历。广度优先遍历则是逐层访问节点，先访问同一层的所有节点，再向下一层继续遍历。

#### 并查集简介

并查集（Disjoint Set）是一种数据结构，用于处理集合的合并及查询元素所属集合的问题。并查集的核心在于维护一个由多个集合组成的数据结构，支持两种操作：查找（Find）和合并（Union）。

##### 并查集的核心要点

并查集的核心在于维护一个由多个不相交集合组成的数据结构，每个集合称为一个连通分量。通过查找操作可以找到元素所属的连通分量（根节点），而合并操作则可将两个不同的连通分量合并为一个。

##### 并查集的相关概念解析

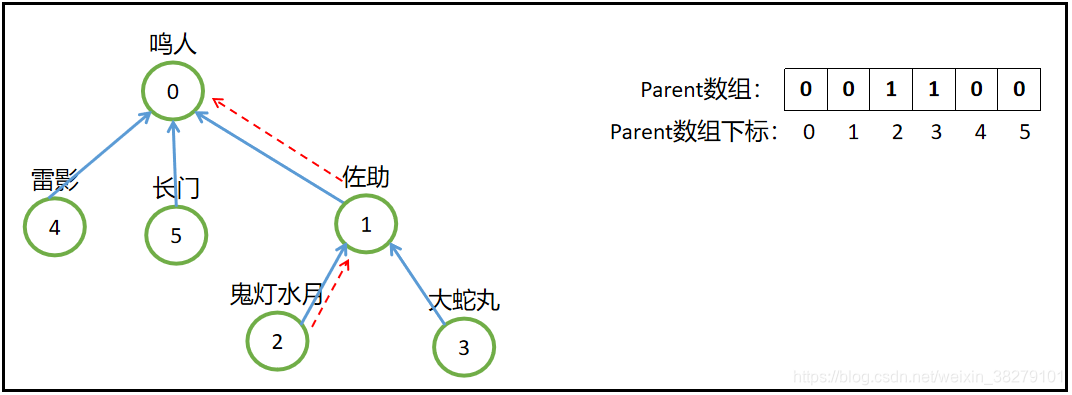
在并查集中，一个集合通常以树的形式表示，每个节点指向其父节点，根节点指向自身。根据根节点是否相同，可以判断元素是否属于同一个集合。路径压缩和按秩合并是优化并查集性能的常用手段，其中路径压缩可以减小树的高度，按秩合并可以减小树的深度。

根据以上基础概念，可以更深入地了解并查集这一数据结构的具体实现和应用。

# 3. **数组存储的并查集实现**

在并查集的实现中，我们可以通过数组来存储节点的信息，这种方法在简单场景下具有一定的优势。首先，我们将了解数组存储结构的基本特点，随后介绍实现方法的具体步骤。

#### 3.1 存储结构

##### 3.1.1 数组的基本特点

数组是一种线性数据结构，以连续的内存空间存储相同类型的元素。数组的元素通过索引进行访问，具有快速随机访问的特点。在实现并查集时，可以通过数组的索引表示节点的编号，利用数组存储节点的相关信息。

##### 3.1.2 数组存储并查集的优势

- **简单高效**：数组存储结构简单直观，操作方便高效。
- **内存紧凑**：数组在内存中连续存储，减少内存碎片，有利于提高访问速度。
- **易于操作**：通过数组下标快速定位节点，实现并查集的操作更加便利。

#### 3.2 实现方法

##### 3.2.1 初始化数组

在实现数组存储的并查集时，首先需要初始化数组。将每个节点表示为一个独立的集合，且每个节点的父节点指向自身，表示该节点为集合的根节点。

# 初始化数组，每个节点的父节点指向自身
def init_parent(n):
    parent = [i for i in range(n)]
    return parent

##### 3.2.2 查找根节点的算法

实现查找根节点的算法时，通过不断向上查找父节点，直到找到根节点为止。根节点的特点是其父节点指向自身。

# 查找根节点的算法
def find(parent, x):
    if parent[x] != x:
        parent[x] = find(parent, parent[x])  # 路径压缩
    return parent[x]

##### 3.2.3 合并操作的实现

合并操作是并查集的核心操作之一，通过将两个集合的根节点合并，实现两个节点之间的连通。

# 合并操作
def union(parent, x, y):
    root_x = find(parent, x)
    root_y = find(parent, y)
    if root_x != root_y:
        parent[root_x] = root_y

通过以上实现方法，可以建立数组存储的并查集，方便进行节点之间的合并与查询操作，提高算法效率。

# 4. 并查集的应用

#### 4.1 连通性判断
在实际生活中，经常需要判断不同节点之间是否具有连通性，而并查集是一种高效的数据结构，可以帮助我们解决这类问题。通过并查集，我们可以在常数时间内判断两个节点是否处于同一个联通分量中。

##### 4.1.1 判断网络中节点是否连通
假设我们有一个网络，其中各个节点之间存在连接关系，我们希望能够快速判断任意两个节点之间是否存在联通路径。通过并查集的方法，我们可以维护一个联通分量，将同一条路径上的所有节点都连接到同一个根节点下。这样，当我们需要判断两个节点是否连通时，只需要查看它们是否具有相同的根节点即可。

##### 4.1.2 应用于最小生成树算法
最小生成树算法是指在一个连通加权图中生成一棵包含所有顶点的树，且边的权值之和最小。在实现最小生成树的过程中，我们可以利用并查集来快速合并不同的子树，并判断是否形成环路，从而避免出现环路而导致生成树不成立的情况。

#### 4.2 社交网络中的应用
在当今的社交网络中，人与人之间的关系错综复杂，而并查集可以帮助我们快速构建并维护这些关系，实现一些便捷的功能。

##### 4.2.1 好友关系的建立
在一个社交网络中，我们可以利用并查集来维护人与人之间的好友关系。当两个人成为好友时，我们可以将它们所在的联通分量合并，这样就可以快速找到任意人的所有好友。同时，通过查找根节点的方法，我们还可以判断两个人之间是否为好友关系。

##### 4.2.2 查找共同朋友的应用
在社交网络中，有时我们需要找到两个人的共同朋友，而这个问题可以通过并查集来解决。我们可以先找到这两个人所在的根节点，然后遍历根节点的所有子节点，将它们保存在一个集合中。最后，比较这两个集合，即可找到这两个人的共同朋友们。

# 5. 总结与展望

在本文中，我们深入探讨了并查集这一数据结构的基本概念、实现原理以及应用场景。通过对树状结构和并查集的详细介绍，我们了解了并查集的核心思想和相关概念。

同时，我们通过实际代码示例，展示了如何使用数组存储来实现并查集，包括初始化数组、查找根节点算法、以及合并操作的具体实现步骤。通过这些实例，读者可以更加深入地理解并查集的内部机制。

在应用部分，我们提到了并查集在连通性判断和社交网络中的应用。从判断网络中节点是否连通到社交网络中好友关系的建立，都展示了并查集在实际场景中的重要性和灵活性。

总的来说，通过本文的学习，读者可以掌握并查集的基本原理和实现方法，了解并查集在解决实际问题中的应用。进一步深入学习数据结构与算法，可以扩展到更复杂的场景和问题，提升自己的编程能力和解决问题的能力。

#### 进一步学习的建议

为了更深入地了解并查集以及其他常见的数据结构与算法知识，读者可以考虑以下学习路径：

1. 深入学习并查集的优化方法，如路径压缩和按秩合并，进一步提高并查集的效率和性能。

2. 学习其他常见的图算法，如最短路径算法、最小生成树算法等，结合并查集，拓展解决各种复杂问题的能力。

3. 参与在线学习平台或算法竞赛，通过实际问题的练习和实战，提升自己的编程技能和算法思维能力。

4. 阅读经典的算法书籍，如《算法导论》、《数据结构与算法分析》等，系统地学习和掌握数据结构与算法的理论知识。

5. 加入算法交流社区或参加相关讨论，与他人交流学习经验、分享解题思路，共同进步和提高编程水平。

通过持续学习和实践，不断提升自己在数据结构与算法领域的能力，成为一个优秀的程序员和问题解决者。愿每位读者在学习路上一帆风顺，探索更广阔的编程世界！