【Java图数据结构】：构建与操作邻接图的秘籍

# 1. 图数据结构基础

## 1.1 图的基本概念

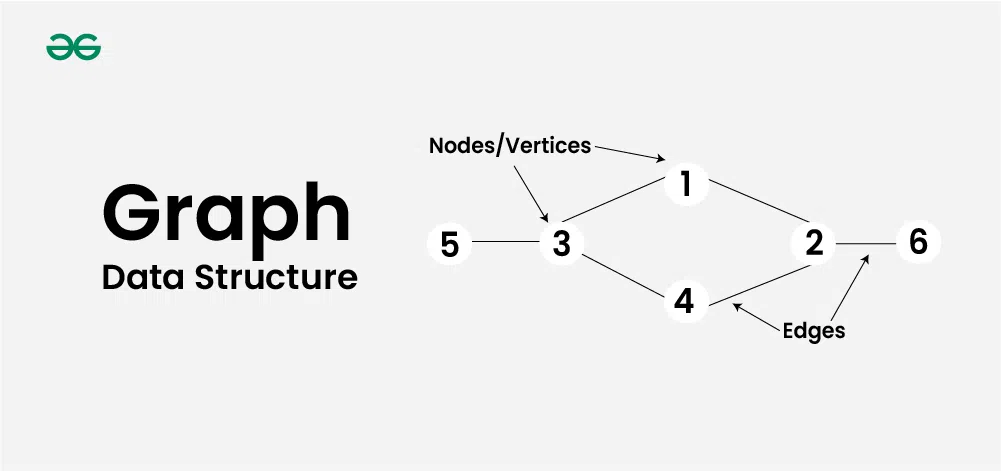
在计算机科学中，图是一种非线性数据结构，用于表示对象之间的一对多关系。图由一组顶点（或节点）和一组连接顶点的边组成。图论是数学的一个分支，研究图的性质和图中顶点与边的关系。

## 1.2 图的表示方法

图可以通过多种方式表示，常见的有邻接矩阵和邻接表。邻接矩阵使用二维数组，其中每个元素表示两个顶点之间是否相邻，而邻接表则使用列表或者链表来表示每个顶点的邻接顶点。

### 1.2.1 邻接矩阵表示法

邻接矩阵是一种紧凑的表示方式，特别适合稠密图。对于无向图，邻接矩阵是对称的。使用邻接矩阵的示例代码如下：

int[][] adjacencyMatrix = {
    {0, 1, 1, 0},
    {1, 0, 1, 1},
    {1, 1, 0, 1},
    {0, 1, 1, 0}
};

### 1.2.2 邻接表表示法

邻接表更适合稀疏图，并且能够节省存储空间。每个顶点用链表来表示其邻接顶点，示例代码如下：

Map<Integer, List<Integer>> adjacencyList = new HashMap<>();
adjacencyList.put(1, Arrays.asList(2, 3));
adjacencyList.put(2, Arrays.asList(1, 3, 4));
adjacencyList.put(3, Arrays.asList(1, 2, 4));
adjacencyList.put(4, Arrays.asList(2, 3));

理解图的表示方法对于后续学习图的操作和算法至关重要。在后续章节中，我们将深入探讨邻接图的理论和实际应用。

# 2. 邻接图的理论基础

## 2.1 图论的核心概念
### 2.1.1 图的定义与分类
图是由一组顶点（或称为节点）以及连接这些顶点的边组成的数据结构。在计算机科学和数学中，图是描述实体之间关系的重要工具，广泛应用于网络理论、社交分析、算法设计等领域。

在图论中，图可按照边的特性分为无向图和有向图。无向图的边没有方向性，表示顶点之间的相互关系；有向图的边是有方向的，表示信息或控制的单向流动。此外，根据边是否存在权重，图可分为加权图和非加权图。加权图中的每条边都有一个数值，称为权重，常用来表示距离、成本或容量等。

### 2.1.2 邻接图的特点和应用场景
邻接图是一种特殊类型的图，其中每个顶点都与其它顶点通过边相连。邻接图适用于表示高度互联的网络结构，例如社交网络、生物网络或某些类型的交通网络。邻接图的特点是它能够捕捉顶点之间的所有可能关系。

邻接图在许多应用中都非常有用。例如，在社交网络分析中，邻接图可用于分析用户的互动模式、发现社群结构以及进行影响力分析。在交通规划中，邻接图能够帮助设计最优的路线，减少旅行时间和成本。在网络理论中，邻接图可以帮助我们更好地理解网络的稳定性和脆弱性。

## 2.2 邻接图的数学模型
### 2.2.1 图的数学表示方法
数学上，无向图可以通过邻接矩阵或邻接表来表示。邻接矩阵是一个二维数组，其中每个元素表示顶点之间的连接情况。若顶点i和顶点j之间存在边，则邻接矩阵的(i, j)位置上为1，否则为0（或对于加权图，填充相应的权重值）。邻接矩阵是一个对称矩阵，适合于表示无向图。

邻接表则是用一系列的列表或链表来存储图中的边。每个顶点有一个关联的链表，链表中的元素表示与该顶点相连的其他顶点。邻接表空间效率更高，特别适合表示稀疏图。

### 2.2.2 邻接矩阵和邻接表的对比分析
邻接矩阵和邻接表各有优势和局限性。邻接矩阵在表示稠密图时空间效率较高，易于判断任意两个顶点之间是否存在直接的连接，且计算较为简单。但是，对于大型稀疏图，邻接矩阵会浪费大量的空间，因为它们需要为图中的所有可能的顶点对都分配空间，无论这些顶点是否真的相连。

邻接表对稀疏图非常友好，因为它只存储实际存在的边。这使得邻接表在内存使用上更加高效。同时，邻接表支持快速的边遍历和插入操作。然而，邻接表并不直接支持对任意两个顶点间路径的快速查询，因为这种查询需要对两个顶点的链表进行遍历，时间复杂度为O(V + E)，其中V是顶点数，E是边数。

在选择使用邻接矩阵还是邻接表时，需要根据图的稠密度、操作类型以及空间和时间的权衡来决定。

# 3. 邻接图的实现技术

## 邻接图的基本操作

### 图的创建与初始化

在讨论邻接图的实现技术之前，我们必须首先理解如何创建和初始化一个图。创建和初始化图是进行图算法操作的第一步，它定义了图的初始状态，包括顶点和边的设置。在计算机科学中，图的实现可以采取多种数据结构，包括邻接矩阵和邻接表等。

以下是使用邻接表实现图的创建与初始化的代码示例（假设使用Java语言）：

import java.util.ArrayList;
import java.util.List;

class Graph {
    private int vertices; // 图的顶点数量
    private List<List<Integer>> adjList; // 邻接表

    // 图的构造函数
    public Graph(int vertices) {
        this.vertices = vertices;
        adjList = new ArrayList<>(vertices);
        for (int i = 0; i < vertices; i++) {
            adjList.add(i, new ArrayList<Integer>());
        }
    }

    // 添加边的操作
    public void addEdge(int src, int dest) {
        adjList.get(src).add(dest); // 将目标顶点添加到源顶点的邻接列表中
    }

    // 用于表示图的字符串方法（用于打印图）
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        for (int i = 0; i < vertices; i++) {
            sb.append(i + " --> ");
            List<Integer> list = adjList.get(i);
            for (Integer v : list) {
                sb.append(v + " ");
            }
            sb.append("\n");
        }
        return sb.toString();
    }
}

在上述代码中，我们定义了一个`Graph`类，它包含顶点数量`vertices`和一个`adjList`作为邻接表。`Graph`的构造函数初始化一个具有指定数量顶点的图，并为每个顶点创建一个空的邻接列表。`addEdge`方法用于在图中添加边，它接受两个参数：`src`（源顶点）和`dest`（目标顶点）。`toString`方法返回一个字符串表示图的内容，便于打印和调试。

### 添加和删除顶点与边

除了创建和初始化图，我们还需要掌握如何在图中添加和删除顶点与边。添加顶点通常涉及到改变邻接表的大小和初始化新的顶点列表。删除顶点则更复杂一些，因为它涉及到更新所有受影响顶点的邻接列表，以移除指向被删除顶点的引用。添加和删除边的操作会根据顶点的索引进行。

下面是添加和删除顶点与边操作的扩展代码：

// 添加顶点的方法
public void addVertex() {
    adjList.add(new ArrayList<Integer>());
}

// 删除顶点的方法
public void removeVertex(int v) {
    // 删除与顶点v相关的所有边
    adjList.remove(v);
    // 更新其他顶点的邻接列表以移除指向顶点v的引用
    for (List<Integer> list : adjList) {
        list.remove(Integer.valueOf(v));
    }
}

// 删除边的方法
public void removeEdge(int src, int dest) {
    adjList.get(src).remove(Integer.valueOf(dest));
}

在此代码片段中，`addVertex`方法在邻接表末尾添加一个新的空列表，代表新的顶点。`removeVertex`方法首先从邻接表中删除被删除顶点的列表，然后遍历每个顶点的列表，删除所有指向该顶点的引用。`removeEdge`方法从源顶点的邻接列表中删除目标顶点的索引。

## 邻接图的高级操作

### 图的遍历算法

图的遍历是图论中的基础操作，也是图算法中最常见的一种。它分为深度优先搜索（DFS）和广度优先搜索（BFS）两种类型。遍历算法的主要目的是访问图中的每个顶点恰好一次。

#### 深度优先搜索（DFS）

深度优先搜索是一种用于遍历或搜索树或图的算法。在搜索过程中，它尽可能深地搜索图的分支。当节点v的所在边都已被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这个过程一直进行到已发现从源节点可达的所有节点为止。

下面是一个DFS算法的实现示例：

import java.util.*;

public void DFS(int v) {
    // 标记顶点v为已访问
    boolean visited[] = new boolean[vertices];
    for (int i = 0; i < vertices; i++) {
        visited[i] = false;
    }
    // 使用递归实现DFS遍历
    DFSUtil(v, visited);
}

private void DFSUtil(int v, boolean visited[]) {
    // 标记当前节点为已访问，并打印它
    visited[v] = true;
    System.out.print(v + " ");

    // 递归访问所有未访问的邻居顶点
    for (int neighbor : adjList.get(v)) {
        if (!visited[neighbor]) {
            DFSUtil(neighbor, visited);
        }
    }
}

在上面的DFS实现中，我们定义了两个方法：`DFS`和`DFSUtil`。`DFS`方法初始化一个布尔数组`visited`，用于跟踪访问过的顶点。`DFSUtil`是一个递归方法，遍历所有未访问的邻居顶点，并递归地调用自身来继续遍历。

#### 广度优先搜索（BFS）

广度优先搜索是一种遍历或搜索树或图的算法。它从根节点开始，然后探索每个邻近的节点，在每个节点被访问后，BFS将访问其未被访问的邻居节点。这种方法使用队列数据结构来跟踪节点的访问顺序。

以下是BFS算法的实现示例：

import java.util.*;

public void BFS(int v) {
    // 标记所有顶点为未访问
    boolean visited[] = new boolean[vertices];

    // 创建一个队列用于BFS
    LinkedList<Integer> queue = new LinkedList<>();

    // 标记当前节点为已访问，并将其加入队列
    visited[v] = true;
    queue.add(v);

    while (queue.size() != 0) {
        // 移除队列的第一个顶点，并打印它
        v = queue.poll();
        System.out.print(v + " ");

        // 获取所有邻接顶点
        for (int neighbor : adjList.get(v)) {
            if (!visited[neighbor]) {
                visited[neighbor] = true;
                queue.add(neighbor);
            }
        }
    }
}

在BFS实现中，我们同样定义了两个方法：`BFS`和一个辅助方法（这里隐藏在`BFS`方法内部）。`BFS`初始化一个布尔数组`visited`和一个队列`queue`。算法首先访问起始顶点并将其加入队列。随后进入一个循环，在队列非空的情况下，循环将继续执行。在循环内部，我们取出队列的第一个顶点，打印它，然后将其所有未访问的邻居顶点加入队列。

### 最短路径与连通性问题解决方案

在图论中，确定两个顶点之间的最短路径是一个经典问题，这在很多实际应用中是非常有用的。有多种算法可以解决最短路径问题，比如Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。这里我们重点讨论Dijkstra算法和Floyd-Warshall算法的实现。

#### Dijkstra算法

Dijkstra算法用于在加权图中找到一个顶点到其他所有顶点的最短路径。这个算法适用于没有负权边的图。

以下是Dijkstra算法的实现示例：

public void dijkstra(int startVertex) {
    // 保存最短路径的权值
    int[] distances = new int[vertices];
    // 保存前驱节点，用于重建最短路径
    int[] predecessors = new int[vertices];
    // 初始化所有距离为无穷大
    Arrays.fill(distances, Integer.MAX_VALUE);
    // 初始化起始点的距离为0
    distances[startVertex] = 0;
    // 用于跟踪所有访问过的顶点
    boolean[] visited = new boolean[vertices];

    for (int i = 0; i < vertices; i++) {
        // 在未访问的顶点中选择距离最小的顶点
        int nearestVertex = -1;
        int shortestDistance = Integer.MAX_VALUE;
        for (int vertex = 0; vertex < vertices; vertex++) {
            if (!visited[vertex] && distances[vertex] < shortestDistance) {
                nearestVertex = vertex;
                shortestDistance = distances[vertex];
            }
        }

        // 标记选中的顶点为已访问
        visited[nearestVertex] = true;

        // 遍历所有邻居顶点，更新距离值
        for (int neighbor : adjList.get(nearestVertex)) {
            int edgeDistance = distances[nearestVertex] + 1; // 假设边的权值为1
            if (edgeDistance < distances[neighbor]) {
                distances[neighbor] = edgeDistance;
                predecessors[neighbor] = nearestVertex;
            }
        }
    }

    // 打印从startVertex到所有顶点的最短路径
    printSolution(startVertex, distances, predecessors);
}

private void printSolution(int startVertex, int[] distances, int[] predecessors) {
    for (int vertex = 0; vertex < vertices; vertex++) {
        if (vertex != startVertex) {
            System.out.println("最短路径从顶点 " + startVertex + " 到顶点 " + vertex
                    + " 的距离是 " + distances[vertex]);
            // 使用predecessors数组重建路径
            printPath(predecessors, startVertex, vertex);
        }
    }
}

private void printPath(int[] predecessors, int startVertex, int endVertex) {
    if (predecessors[endVertex] == startVertex) {
        System.out.print(startVertex);
    } else {
        printPath(predecessors, startVertex, predecessors[endVertex]);
        System.out.print(" -> " + endVertex);
    }
}

在该实现中，我们首先初始化所有顶点到`startVertex`的距离为无穷大，将`startVertex`的距离设置为0，并创建一个`visited`数组以标记已访问的顶点。算法主体是一个循环，它重复以下步骤，直到所有顶点都被访问：找到未访问的顶点中距离`startVertex`最近的顶点，并更新所有其邻居的距离。`printSolution`方法打印出所有从`startVertex`出发的最短路径。

#### Floyd-Warshall算法

Floyd-Warshall算法是一个经典的动态规划算法，用于求解图中所有顶点对之间的最短路径问题。

以下是Floyd-Warshall算法的实现示例：

public void floydWarshall() {
    // 初始化距离矩阵，distanceMatrix[i][j]代表i到j的直接距离
    int[][] distanceMatrix = new int[vertices][vertices];
    for (int[] row : distanceMatrix) {
        Arrays.fill(row, Integer.MAX_VALUE);
    }

    // 初始化前驱矩阵，predecessorMatrix[i][j]记录i到j的最短路径上的前驱节点
    int[][] predecessorMatrix = new int[vertices][vertices];
    for (int[] row : predecessorMatrix) {
        Arrays.fill(row, -1);
    }

    // 初始化距离矩阵
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            if (i == j) {
                distanceMatrix[i][j] = 0;
            } else if (adjList.get(i).contains(j)) {
                distanceMatrix[i][j] = 1; // 假设边的权值为1
                predecessorMatrix[i][j] = j;
            }
        }
    }

    // Floyd-Warshall算法核心部分
    for (int k = 0; k < vertices; k++) {
        for (int i = 0; i < vertices; i++) {
            for (int j = 0; j < vertices; j++) {
                if (distanceMatrix[i][k] != Integer.MAX_VALUE && distanceMatrix[k][j] != Integer.MAX_VALUE && distanceMatrix[i][k] + distanceMatrix[k][j] < distanceMatrix[i][j]) {
                    distanceMatrix[i][j] = distanceMatrix[i][k] + distanceMatrix[k][j];
                    predecessorMatrix[i][j] = predecessorMatrix[i][k];
                }
            }
        }
    }

    // 打印所有顶点对之间的最短路径
    printFloydWarshallResults(distanceMatrix, predecessorMatrix);
}

private void printFloydWarshallResults(int[][] distanceMatrix, int[][] predecessorMatrix) {
    for (int i = 0; i < vertices; i++) {
        for (int j = 0; j < vertices; j++) {
            if (distanceMatrix[i][j] == Integer.MAX_VALUE) {
                System.out.print("INF ");
            } else {
                System.out.print(distanceMatrix[i][j] + " ");
            }
        }
        System.out.println();
    }
    System.out.println();
}

在这个Floyd-Warshall算法实现中，我们创建了一个二维数组`distanceMatrix`来存储每对顶点之间的距离，以及一个二维数组`predecessorMatrix`用于跟踪最短路径的前驱节点。算法的主体是三个嵌套的循环，其中实现了Floyd-Warshall算法的核心动态规划思想。`printFloydWarshallResults`方法打印出图中所有顶点对之间的最短路径长度。

### 最短路径与连通性问题的表格分析

在探讨最短路径与连通性问题时，表格成为一种强大的工具，它可以帮助我们更清晰地理解问题和解决方案。以下是一个描述Dijkstra算法中距离和前驱更新过程的表格示例：

| 顶点 | 距离起始点距离 | 前驱顶点 |
|------|----------------|----------|
| V0 | 0 | - |
| V1 | ∞ | - |
| V2 | ∞ | - |
| ... | ... | ... |
| Vn | ∞ | - |

在上面的表格中，列出了所有顶点的当前最短距离和前驱节点。每次循环，最短路径更新时，表格中的值也随之更新。这种表格不仅适用于Dijkstra算法，也可以用于描述其他图算法的状态变化。

### 最短路径与连通性问题的流程图展示

Mermaid格式流程图可以用来描述算法的工作流程。以下是一个简化的Dijkstra算法流程图：

graph TD
    A[开始] --> B{遍历未访问顶点}
    B -->|找到最短距离顶点| C[更新距离和前驱]
    C --> D[访问顶点]
    D --> B
    B -->|所有顶点访问完毕| E[结束]

在上述流程图中，算法首先开始遍历所有未访问的顶点，寻找距离起始点最近的顶点，并更新距离和前驱信息。接着访问选定的顶点，并重复这个过程，直到所有顶点都访问完毕。

通过这些具体的实现和分析方法，我们深入地探索了邻接图的高级操作，展示了图的遍历算法和最短路径与连通性问题的解决方案。这些技术构成了邻接图技术实现的核心，是进行更复杂图操作和分析的基础。

# 4. 邻接图在Java中的应用

## 4.1 Java图数据结构的实现

### 4.1.1 使用Java集合框架构建图

图的实现依赖于顶点和边的集合，Java集合框架提供了灵活的数据结构来满足这样的需求。在Java中，我们可以使用`List`或`Set`来存储顶点，同时使用`Map`来存储边。例如，使用`HashMap`可以方便地通过顶点来访问其相邻的顶点集合。

下面是一个使用Java集合框架构建图的简单示例：

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;

class Graph {
    private Map<Integer, Set<Integer>> adjList; // 邻接表

    public Graph() {
        adjList = new HashMap<>();
    }

    public void addVertex(int vertex) {
        adjList.put(vertex, new HashSet<>());
    }

    public void addEdge(int source, int destination) {
        if (!adjList.containsKey(source)) {
            addVertex(source);
        }
        if (!adjList.containsKey(destination)) {
            addVertex(destination);
        }
        adjList.get(source).add(destination);
        // 如果是有向图，需要添加到两个顶点的邻接表
        // adjList.get(destination).add(source);
    }

    public void removeEdge(int source, int destination) {
        if (!adjList.containsKey(source)) {
            return;
        }
        adjList.get(source).remove(destination);
        // 如果是有向图，还需要从另一个邻接表中移除
        // adjList.get(destination).remove(source);
    }
}

// 使用示例
public class Main {
    public static void main(String[] args) {
        Graph g = new Graph();
        g.addVertex(0);
        g.addVertex(1);
        g.addEdge(0, 1);
        // 图中现在有顶点0和顶点1，以及一条从0到1的边
    }
}

在这个例子中，我们定义了一个`Graph`类，它使用`HashMap`来存储一个邻接表。每个顶点都映射到一个`HashSet`，该集合存储了与该顶点相邻的顶点。`addVertex`方法用于添加一个新顶点，而`addEdge`方法用于在两个顶点之间添加一条边。我们可以看到，使用Java的集合框架可以方便地构建和管理图的结构。

### 4.1.2 图操作的封装与优化

为了更好地封装图操作，我们可以实现一些辅助方法来提高代码的可读性和可维护性。例如，我们可以添加方法来打印图，或者检查两个顶点是否直接相连。优化则可以通过缓存来实现，比如在实现路径查找算法时，我们可以缓存已经计算过的结果以避免重复计算。

class Graph {
    // ...之前的代码...

    public void printGraph() {
        for (Map.Entry<Integer, Set<Integer>> entry : adjList.entrySet()) {
            System.out.println(entry.getKey() + " is connected to " + entry.getValue());
        }
    }

    public boolean hasEdge(int source, int destination) {
        return adjList.containsKey(source) && adjList.get(source).contains(destination);
    }
    // ...更多的辅助方法...
}

// 使用示例
public class Main {
    public static void main(String[] args) {
        Graph g = new Graph();
        // ...添加顶点和边...
        g.printGraph(); // 打印图的邻接表表示
        System.out.println(g.hasEdge(0, 1)); // 检查是否0和1之间有边
    }
}

在上面的代码中，我们向`Graph`类中添加了两个辅助方法：`printGraph`和`hasEdge`。`printGraph`方法用于打印图的邻接表表示，而`hasEdge`方法用于检查两个顶点之间是否存在边。通过这样的封装，我们不仅提升了代码的可用性，也使得图的操作更加直观。

## 4.2 邻接图算法实战

### 4.2.1 实现图的常见算法

图是数据结构和算法领域的一个核心主题，包括很多经典的算法，如深度优先搜索（DFS）、广度优先搜索（BFS）、最短路径算法（如Dijkstra算法）、最小生成树算法（如Kruskal算法），以及动态规划中的Floyd-Warshall算法等。

我们以Dijkstra算法为例，演示如何在Java中实现这一算法来寻找图中两点间的最短路径。Dijkstra算法适用于带权重的有向或无向图，并且所有边的权重必须为非负数。

下面是Dijkstra算法的实现示例：

import java.util.Arrays;
import java.util.PriorityQueue;

class Edge {
    public final int to;
    public final int weight;
    public Edge(int to, int weight) {
        this.to = to;
        this.weight = weight;
    }
}

class DijkstraResult {
    public final int[] distances;
    public final int[] parents;

    public DijkstraResult(int[] distances, int[] parents) {
        this.distances = distances;
        this.parents = parents;
    }
}

public class GraphAlgorithms {
    public static DijkstraResult dijkstra(int start, Map<Integer, Set<Edge>> graph) {
        int size = graph.size();
        int[] distances = new int[size];
        int[] parents = new int[size];
        Arrays.fill(distances, Integer.MAX_VALUE);
        distances[start] = 0;

        PriorityQueue<Edge> queue = new PriorityQueue<>((a, b) -> ***pare(a.weight, b.weight));
        queue.offer(new Edge(start, 0));

        while (!queue.isEmpty()) {
            Edge currentEdge = queue.poll();
            int currentIndex = currentEdge.to;
            if (distances[currentIndex] < currentEdge.weight) {
                continue; // 如果当前距离大于边的权重，则跳过
            }
            for (Edge edge : graph.get(currentIndex)) {
                int nextIndex = edge.to;
                int nextWeight = currentEdge.weight + edge.weight;
                if (nextWeight < distances[nextIndex]) {
                    distances[nextIndex] = nextWeight;
                    parents[nextIndex] = currentIndex;
                    queue.offer(new Edge(nextIndex, nextWeight));
                }
            }
        }
        return new DijkstraResult(distances, parents);
    }
}

在这个实现中，我们定义了一个辅助类`Edge`来表示图中的边，包括目标顶点和权重。`DijkstraResult`类用于存储算法结果，包括每个顶点到起点的最短距离和路径的父顶点。`dijkstra`方法实现了Dijkstra算法，使用优先队列来保持当前已知最短路径的顶点，并更新队列中其他顶点的距离和父顶点。

### 4.2.2 应用案例分析

让我们通过一个实际案例来分析邻接图在社交网络分析中的应用。假设我们正在构建一个社交网络平台，我们需要实现一个功能来找出两个用户之间的最短路径，以便用户可以查看他们之间的连接度。另一个应用可能是查找两个城市之间的最短旅行路径。

考虑一个简化场景，有一个由用户构成的小型社交网络，我们想用Dijkstra算法找出两个用户之间的最短路径。在实现时，我们需要将用户转换为图中的顶点，用户之间的关系转换为带权重的边，其中权重代表用户之间的亲近程度或互动频率。

import java.util.HashMap;
import java.util.HashSet;
import java.util.Map;
import java.util.Set;

public class SocialNetworkAnalysis {
    public static void main(String[] args) {
        Map<Integer, Set<Edge>> graph = new HashMap<>();
        // ...添加边来表示社交网络中用户之间的连接关系...

        int startUserId = 0;
        int endUserId = 4;
        DijkstraResult result = GraphAlgorithms.dijkstra(startUserId, graph);

        int distance = result.distances[endUserId];
        System.out.println("The shortest distance is " + distance);

        // 输出路径
        int at = endUserId;
        while (at != startUserId) {
            at = result.parents[at];
            System.out.println("User " + at + " is an intermediary to the target.");
        }
    }
}

在这个代码段中，我们首先构建了一个图，用以表示社交网络中用户之间的连接关系。然后，我们使用`dijkstra`方法计算了从一个用户（`startUserId`）到另一个用户（`endUserId`）的最短路径。最后，我们输出了最短路径的长度和路径上的中间用户。

通过这样的应用案例，我们可以看到邻接图在实际问题中的强大应用潜力，以及如何将理论算法有效地应用于解决现实世界的问题。

# 5. 邻接图的优化与挑战

邻接图作为图数据结构的重要表现形式，在许多应用领域如社交网络、生物信息学、网络路由等中扮演着关键角色。然而，随着应用场景的复杂化和数据规模的扩大，邻接图面临着性能优化和设计改进的挑战。本章节将深入探讨邻接图的性能优化策略、面向对象设计原则的应用，以及邻接图在现实应用中遇到的挑战。

## 5.1 邻接图性能优化策略

性能优化是软件开发中的永恒话题，对于数据结构和算法而言尤其如此。邻接图作为一种数据结构，在空间复杂度和时间复杂度上有其固有的瓶颈，优化这些方面可以显著提升算法效率和系统性能。

### 5.1.1 空间复杂度优化

空间复杂度主要关注算法在执行过程中所需要的存储空间。对于邻接图而言，空间复杂度的优化通常集中在如何高效地表示图结构上。

**代码块示例：**

// 使用邻接表代替邻接矩阵表示图结构，降低空间占用
class Graph {
    private Map<Integer, List<Integer>> adjacencyList;

    public Graph() {
        adjacencyList = new HashMap<>();
    }

    public void addEdge(int source, int destination) {
        ***puteIfAbsent(source, k -> new ArrayList<>()).add(destination);
    }
}

**逻辑分析与参数说明：**
上述代码通过使用`HashMap`和`ArrayList`实现了邻接表的存储结构，这比使用二维数组实现的邻接矩阵更加节省空间，特别是对于稀疏图而言。邻接表只存储存在的边，而邻接矩阵不管图是否稀疏，都需要存储矩阵大小的数组空间。

### 5.1.2 时间复杂度优化

时间复杂度关注算法执行的效率。在图的搜索、遍历和路径查找等操作中，优化时间复杂度可以显著提升算法性能。

**代码块示例：**

// 使用深度优先搜索（DFS）进行图遍历，优化时间复杂度
void dfs(int node, boolean[] visited) {
    visited[node] = true;
    System.out.println(node);

    for (int neighbor : adjacencyList.getOrDefault(node, Collections.emptyList())) {
        if (!visited[neighbor]) {
            dfs(neighbor, visited);
        }
    }
}

**逻辑分析与参数说明：**
该代码段展示了如何使用DFS遍历图结构。DFS在某些场景下比广度优先搜索（BFS）更加节省内存，特别是在路径查找时能够更快地收敛。在实现时，通过递归和避免重复访问来优化时间复杂度。

## 5.2 面向对象的设计原则在邻接图中的应用

面向对象的设计原则提供了设计良好软件系统的蓝图。在图数据结构的实现中，合理应用这些原则可以带来更高的可维护性和可扩展性。

### 5.2.1 设计模式在图结构中的应用

设计模式是面向对象设计中解决特定问题的一般性解决方案。在图数据结构的设计中，单例模式、工厂模式、策略模式等都很常见。

**代码块示例：**

// 应用工厂模式创建不同类型的图对象
class GraphFactory {
    public static Graph createGraph(String type) {
        switch (type) {
            case "UNDIRECTED":
                return new UndirectedGraph();
            case "DIRECTED":
                return new DirectedGraph();
            default:
                throw new IllegalArgumentException("Unknown graph type");
        }
    }
}

**逻辑分析与参数说明：**
通过工厂模式，可以灵活地创建不同类型的图结构对象。这样的设计使得系统的扩展性和维护性得到提升，比如在添加新的图类型时，无需修改现有代码。

### 5.2.2 图数据结构的可扩展性与维护性

在设计图数据结构时，考虑其可扩展性与维护性至关重要。通过合理的设计，可以使得图结构在未来可以轻松地扩展新功能而不影响现有功能。

**mermaid格式流程图示例：**

graph TD
    A[开始] --> B[定义基本图接口]
    B --> C[实现具体图类]
    C --> D[定义扩展点]
    D --> E[实现扩展功能]
    E --> F[结束]

**逻辑分析：**
流程图展示了如何通过接口和扩展点设计图数据结构以增强其可扩展性和可维护性。首先定义基本的图接口，然后通过实现具体图类来具体化图结构。定义扩展点来保留未来可能的功能扩展，最后实现这些扩展功能以满足新需求。

通过上述章节的分析，我们可以看到邻接图在实际应用中不仅需要考虑基础的实现，还要考虑性能优化和设计原则的应用。接下来的章节将介绍邻接图在未来的研究方向和前沿技术，以及它们如何影响邻接图的发展和应用。

# 6. 邻接图的未来趋势与研究方向

随着信息技术的不断发展，数据结构和算法也在不断地演变，以适应日益增长的计算需求和数据复杂性。邻接图作为一种重要的数据结构，其未来趋势和研究方向已经引起了学术界和工业界的广泛关注。本章将重点讨论邻接图的新发展以及未来可能的研究方向。

## 6.1 新型数据结构对邻接图的影响

### 6.1.1 分布式图数据库

随着大数据时代的到来，分布式系统成为了存储和处理大规模图数据的重要方式。分布式图数据库如Google的Pregel、Apache Giraph和Neo4j等，提供了在多个机器上存储和处理图数据的能力。它们通常采用分片(sharding)技术，将一个大的图数据分散存储在不同的物理节点上，以此来提高数据处理的可扩展性和高可用性。

分布式图数据库对邻接图的影响主要体现在以下几个方面：

- **可扩展性**: 分布式系统能够在增加更多硬件资源的情况下，线性地提高计算和存储能力。
- **容错性**: 通过数据的多副本存储以及故障转移机制，分布式系统能够提供更高的可靠性。
- **并行处理**: 邻接图中的数据可以分布在不同的节点上，并行地进行计算和查询，提高效率。

// 示例代码：展示如何在Apache Giraph中创建一个简单的图计算作业
public class MyVertexProgram extends BaseVertexProgram<LongWritable, NullWritable, LongWritable> {
    @Override
    public boolean start Vertex() {
        setAggregator("sum", new SumAggregator<LongWritable>());
        setCombiner("sum", new SumAggregator<LongWritable>());
        return true;
    }

    @Override
    public boolean vertexProgram(LongWritable vertexValue, MessageScope scope) {
        if (getSuperstep() == 0) {
            sendMessageToAllEdges(scope, vertexValue);
        } else {
            long sum = 0;
            for (MessageScope.Receiver receiver : scope.getReceivers()) {
                sum += getMessage(receiver).get();
            }
            AggregateContext<LongWritable, NullWritable, LongWritable> context = getAggregationContext("sum");
            context.sendUpdateToSelf(sum);
        }
        return true;
    }

    @Override
    public boolean combine(Iterator<LongWritable> messages, MessageScope scope) {
        long sum = 0;
        while (messages.hasNext()) {
            sum += messages.next().get();
        }
        AggregateContext<LongWritable, NullWritable, LongWritable> context = getCombinerContext("sum");
        context.sendUpdateToSender(sum);
        return true;
    }
}

### 6.1.2 图计算框架

图计算框架为图数据处理提供了高效的工具和算法。例如，Apache Giraph和Neo4j等，它们提供了丰富的API和算法库，使得开发人员可以更专注于业务逻辑，而无需从零开始编写基础算法。

- **算法库**: 这些框架通常预置了多种图处理算法，如PageRank、最短路径、连通分量等。
- **优化机制**: 为了高效处理大规模图数据，这些框架在内存管理、网络通信和数据存储等方面进行了大量优化。
- **易用性**: 提供了高级的抽象，隐藏了底层的复杂性，简化了图数据处理程序的开发和维护。

## 6.2 邻接图研究的前沿方向

### 6.2.1 图神经网络（GNN）的基础与应用

图神经网络是一种新兴的深度学习方法，它能够处理具有任意结构的图数据。在GNN模型中，节点和边的信息通过神经网络层进行传递和更新，最终每个节点学习到一个固定长度的向量表示，这个表示能够捕捉图的拓扑结构和节点间的关系。

GNN的研究前沿方向包括但不限于：

- **模型架构**: 如何设计更加有效的GNN模型，以提高学习表示的质量和训练效率。
- **无监督学习**: 探索在没有标签的情况下，如何通过图结构学习到有用的节点特征表示。
- **可解释性**: 提高模型的可解释性，以便理解模型的决策过程。

### 6.2.2 高维图数据的可视化与交互技术

随着图数据规模和复杂性的增加，如何有效地可视化和交互成为了一个挑战。研究者正在开发新的技术和方法，旨在帮助用户更好地理解和分析高维图数据。

- **交互式可视化**: 开发更加直观、响应式的用户界面，以支持交互式探索和分析图数据。
- **多维度信息融合**: 如何将图中的多种信息，如节点属性、边权重等，融合到可视化的表示中。
- **性能优化**: 通过空间分割、聚类等技术，减少可视化过程中对计算资源的消耗，提高渲染效率。

graph TD
    A[开始] --> B[收集图数据]
    B --> C[计算节点布局]
    C --> D[定义节点和边的颜色、形状等属性]
    D --> E[交互式探索与分析]
    E --> F[可视化高维信息]
    F --> G[反馈调整]
    G --> H[结束]

邻接图在未来的研究和应用中，无疑会成为处理复杂数据关系的重要工具。随着技术的不断进步和新算法的提出，我们可以预见邻接图将在数据科学、社交网络、生物信息学等众多领域发挥更大的作用。