【Java网络流算法】：Ford-Fulkerson实现与图数据结构应用

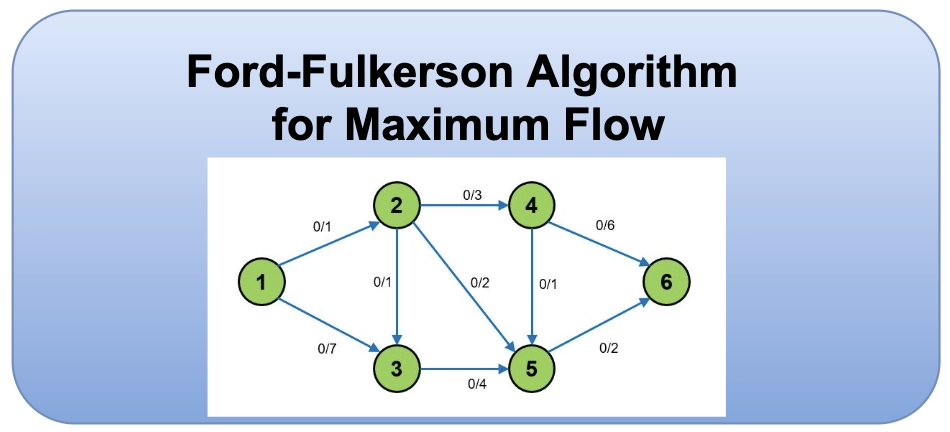
# 1. Java网络流算法与Ford-Fulkerson方法

## 1.1 Java中的网络流与算法需求

网络流问题在现实世界中无处不在，从计算机网络数据包的传输到交通网络的流量优化，网络流算法为我们提供了解决这些问题的数学模型和计算工具。在Java中实现网络流算法，特别是经典的Ford-Fulkerson方法，能够帮助我们解决一系列优化问题，如最大流问题、最小割问题等。通过学习和掌握这些算法，开发者不仅能够扩展他们在图论和网络优化方面的知识，还可以在实际工作中应用这些知识来设计和优化复杂系统。

## 1.2 Ford-Fulkerson方法的原理

Ford-Fulkerson方法是一种通过不断寻找增广路径来增加流的算法，直到再也找不到增广路径为止。该方法的核心在于利用残留网络的概念，每一次迭代都是在寻找在当前流量情况下，是否存在一条路径可以使得流量进一步增加。算法的效率依赖于寻找增广路径的方法。在Java中，我们可以使用深度优先搜索（DFS）或广度优先搜索（BFS）来实现这一点。

## 1.3 Java实现的意义与挑战

在Java中实现Ford-Fulkerson方法不仅可以加深对网络流问题的理解，还可以提升解决实际问题的能力。然而，这种算法的实现也面临着一些挑战，比如如何有效地表示图和流网络、如何优化寻找增广路径的过程等。对于有经验的IT从业者而言，理解和掌握这种算法背后的原理，以及如何在Java中进行高效的编码实现，是一项值得探索的挑战。

# 2. 图数据结构基础

### 2.1 图的基本概念

#### 2.1.1 图的定义和表示

图（Graph）是一种非线性数据结构，它由顶点（Vertices）和边（Edges）组成。顶点通常用小写字母表示，边用连接两个顶点的线表示。在图论中，图可以是有向的（directed），也可以是无向的（undirected）。有向图中的边具有方向性，通常表示为一条从一个顶点到另一个顶点的单箭头线，无向图中的边则表示为无方向的线。

图可以表示为邻接矩阵或邻接表。邻接矩阵使用一个二维数组表示顶点之间的连接关系，矩阵中的元素表示是否存在边，对于有权重的图，元素还表示边的权重。邻接表则使用链表来表示每个顶点的邻接顶点，它更适合表示稀疏图。

// 邻接矩阵表示法的简单实现
public class Graph {
    private int[][] adjacencyMatrix;
    private int vertices;

    public Graph(int vertices) {
        this.vertices = vertices;
        adjacencyMatrix = new int[vertices][vertices];
    }

    public void addEdge(int source, int destination) {
        adjacencyMatrix[source][destination] = 1; // 有向图
    }

    public void printGraph() {
        for (int[] row : adjacencyMatrix) {
            for (int val : row) {
                System.out.print(val + " ");
            }
            System.out.println();
        }
    }
}

#### 2.1.2 图的遍历算法

图的遍历算法有深度优先搜索（DFS）和广度优先搜索（BFS）。DFS通过递归方式遍历所有顶点，而BFS使用队列结构来实现逐层访问。

// 深度优先搜索示例
public void DFS(int vertex) {
    boolean[] visited = new boolean[vertices];
    DFSUtil(vertex, visited);
}

private void DFSUtil(int vertex, boolean[] visited) {
    visited[vertex] = true;
    System.out.print(vertex + " ");

    for (int i = 0; i < vertices; i++) {
        if (adjacencyMatrix[vertex][i] == 1 && !visited[i]) {
            DFSUtil(i, visited);
        }
    }
}

// 广度优先搜索示例
public void BFS(int startVertex) {
    boolean[] visited = new boolean[vertices];
    Queue<Integer> queue = new LinkedList<>();
    visited[startVertex] = true;
    queue.offer(startVertex);

    while (!queue.isEmpty()) {
        int currentVertex = queue.poll();
        System.out.print(currentVertex + " ");

        for (int i = 0; i < vertices; i++) {
            if (adjacencyMatrix[currentVertex][i] == 1 && !visited[i]) {
                visited[i] = true;
                queue.offer(i);
            }
        }
    }
}

### 2.2 加权图和最短路径

#### 2.2.1 加权图的特点

加权图是图的一种，其边被赋予了权重（weight）。这些权重代表了连接顶点的边的重要性或距离。在最短路径问题中，目标是在两个顶点之间找到一条权重和最小的路径。

#### 2.2.2 最短路径算法概述

为了找到加权图中的最短路径，可以使用多种算法，如Dijkstra算法、Bellman-Ford算法等。Dijkstra算法适用于没有负权边的图，而Bellman-Ford算法可以处理带有负权边的图，但不能有负权环。

### 2.3 网络流与割的理论基础

#### 2.3.1 流网络的定义

流网络是图的一种特殊形式，通常表示为G=(V,E,c,s,t)。V表示顶点集合，E表示边集合，c表示边的容量函数，s表示源点，t表示汇点。在网络流中，每条边都有一个容量限制，而流的值不能超过这个容量。

#### 2.3.2 割的定义和性质

割在网络流问题中表示为一组边的集合，当从图中移除这些边后，会使得从源点到汇点的流量降低。割的容量是割中所有边容量的和。最小割问题是找到使得从源点到汇点的流量最小的割。

通过定义和理解图数据结构的基础，我们为后续深入分析Ford-Fulkerson算法及其应用建立了坚实的基础。接下来的章节将介绍算法的理论细节和实现。

# 3. Ford-Fulkerson算法理论详解

## 3.1 算法原理和步骤

### 3.1.1 增广路径的概念

在Ford-Fulkerson算法中，增广路径是指从源点到汇点的一条路径，在这条路径上，每条边都至少有一个未达到其容量限制的"余量"。这样的路径能够允许更多的流量从源点流向汇点，增加网络中整体的流量。寻找增广路径是Ford-Fulkerson算法的核心任务之一，它是迭代进行的，直到无法再找到增广路径为止。

增广路径的寻找通常利用深度优先搜索（DFS）或广度优先搜索（BFS）算法实现。在算法的每次迭代中，我们尝试在网络中增加流量，直到找到一条增广路径或确认网络已经饱和，无法增加更多的流量。

### 3.1.2 算法的迭代过程

Ford-Fulkerson算法是一个迭代过程，每一步迭代中都会尝试增加网络中的流量。以下是算法的详细步骤：

1. 初始化网络流量为零。
2. 持续执行以下步骤，直到网络无法进行进一步的流量增加：
- 在当前流量条件下，寻找一条增广路径。
- 如果找到了增广路径，沿着这条路径增加流量。
- 更新网络中的残余容量。
3. 当无法再找到增广路径时，算法结束，当前的流量就是网络的最大流量。

## 3.2 算法的复杂度分析

### 3.2.1 时间复杂度的影响因素

Ford-Fulkerson算法的时间复杂度主要取决于增广路径的寻找过程。如果使用深度优先搜索（DFS），算法的时间复杂度可以达到O(EF)，其中E是网络中的边数，F是网络的最大流量。这主要是因为每次找到一条增广路径后，流量可能只增加一个非常小的量，这意味着算法需要执行很多次迭代才能达到最大流量。

如果使用广度优先搜索（BFS）来寻找增广路径，时间复杂度可以优化到O(VE^2)，其中V是网络中的顶点数。这是因为在每次迭代中，BFS可以在O(E)时间内找到一条最短的增广路径（即边数最少的路径），而总的迭代次数则受限于每条边的容量乘以边的数量。

### 3.2.2 最坏情况分析

在最坏的情况下，Ford-Fulkerson算法的性能会受到限制。比如在每次迭代中只增加极小的流量，算法需要进行大量的迭代才能确定网络的最大流。例如，在一个简单的网络中，如果每个增广路径只增加单位流量，那么算法的迭代次数将是O(EF)。在最坏的情况下，即网络的容量非常小，这个复杂度是不可接受的。

## 3.3 算法优化策略

### 3.3.1 Edmonds-Karp算法的改进

Edmonds-Karp算法是Ford-Fulkerson方法的一个改进版本，它使用广度优先搜索（BFS）来寻找增广路径。Edmonds-Karp算法克服了Ford-Fulkerson算法在最坏情况下时间复杂度较高的问题。通过利用BFS来寻找最短的增广路径（即边数最少的路径），它保证了算法的每一步迭代都尽可能地增加流量，从而减少迭代的次数。

以下是Edmonds-Karp算法的伪代码：

function EdmondsKarp(graph, source, sink):
    for each edge in graph.edges:
        edge.flow = 0
    while there is a path from source to sink in graph.residual:
        path = BFS(graph.residual, source, sink)
        bottleneck = min(edge.capacity - edge.flow for edge in path)
        for edge in path:
            edge.flow += bottleneck
            edge.reverse.flow -= bottleneck
    return sum(edge.flow for edge in graph.edges starting from source)

### 3.3.2 Dinic算法和Push-relabel算法简介

除了Edmonds-Karp算法之外，还有一些其他的优化策略。比如Dinic算法和Push-relabel算法：

- **Dinic算法**：该算法进一步优化了寻找增广路径的过程，它在每次迭代中使用BFS构造一个层次图，然后在这个层次图中寻找增广路径。Dinic算法的时间复杂度为O(V^2E)。
- **Push-relabel算法**：这种算法使用了不同的方法来实现最大流的计算，它不依赖于增广路径的概念，而是通过"推"和"标签"操作来增加流量。它的工作机制是局部的，可以避免全局搜索增广路径的过程。Push-relabel算法的时间复杂度为O(V^2√E)。

通过这些改进，算法能够以更加高效的