精确剂量计算：掌握离子注入技术提升集成电路性能


# 摘要
本文系统地介绍了离子注入技术的基础理论、精确剂量计算的框架、实际操作流程以及集成电路性能提升的案例研究。首先，概述了离子注入技术的基本原理和计算模型，并探讨了剂量分布优化和精度影响因素。接着，重点阐述了实验操作中的设备与材料准备、剂量控制技术，以及结果的分析与评估方法。随后，通过先进集成电路设计要求，探讨了离子注入工艺的优化和典型工艺流程。最后，展望了离子注入技术的未来趋势，特别是在新型材料应用、3D集成技术以及精确剂量控制策略方面的创新方向，并提出了相应的策略与建议。本文对于理解和应用离子注入技术，尤其是其在提升集成电路性能中的作用具有重要指导意义。

# 关键字
离子注入技术；剂量计算；工艺优化；集成电路；3D集成；材料科学

参考资源链接：[离子注入技术：原理、分布与影响](https://wenku.csdn.net/doc/2s8wjgaei0?spm=1055.2635.3001.10343)
# 1. 离子注入技术基础

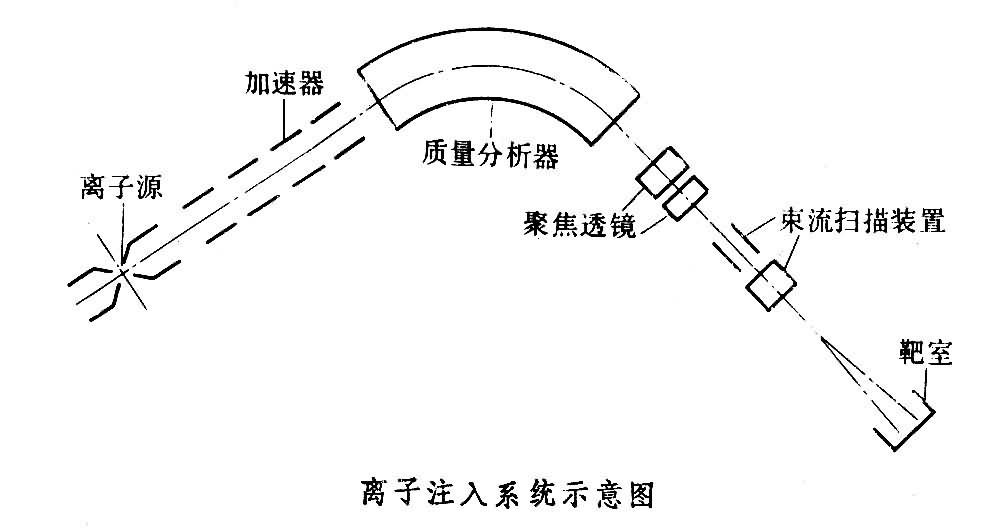
在当今的微电子领域，离子注入技术是实现精确半导体掺杂的关键方法。该技术通过将离子加速并注入到半导体材料中，改变其电学性质，为现代集成电路的制造提供了必不可少的工艺支持。离子注入过程可以控制掺杂离子的种类、能量和剂量，从而实现对半导体特性的精细调控。本章旨在为读者打下理解离子注入技术的基础，为进一步深入学习精确剂量计算、实践操作及未来技术趋势等主题奠定基石。

# 2. 精确剂量计算的理论框架

在现代半导体制造工艺中，离子注入技术是实现精确掺杂的关键环节。为了确保离子注入过程的精确度和重复性，必须建立在严谨的理论基础上进行精确剂量的计算。本章将对这一理论框架进行深入的探讨。

## 2.1 物理原理与剂量计算

### 2.1.1 离子束与物质的相互作用

离子束与固体物质相互作用是一个复杂的过程，包括了一系列的物理和化学反应。从物理角度来讲，离子束在物质中主要通过库仑散射和核散射进行传播。库仑散射是由电子的库仑场引起的，通常主导在较浅的深度，而核散射则是由原子核的相互作用引起的，通常影响更深的区域。

graph LR
    A[离子束入射] -->|电子库仑散射| B[表面散射]
    A -->|原子核散射| C[深度分布]
    B -->|电子密度高| D[浅层掺杂]
    C -->|原子核密度高| E[深层掺杂]

### 2.1.2 剂量计算的基本公式与参数

剂量计算在离子注入过程中起到了至关重要的作用。一般而言，剂量计算公式基于SRIM理论（Stopping and Range of Ions in Matter），计算公式通常为：

D = (Φ * t * NA * ρ) / M

其中：

- `D` 代表剂量（ions/cm²）
- `Φ` 代表离子束流密度（ions/cm²·s）
- `t` 代表注入时间（s）
- `NA` 代表阿伏伽德罗常数
- `ρ` 代表材料密度（g/cm³）
- `M` 代表目标材料的摩尔质量（g/mol）

这里，剂量表示在单位面积内注入的离子总数，而计算的准确性依赖于对离子束流密度和注入时间的精确测量。

## 2.2 剂量分布模型与优化

### 2.2.1 剂量分布模型的建立

剂量分布模型是通过理论推导和实验数据建立的，用于描述离子在固体中分布的数学模型。根据不同的应用需求和材料特性，可以建立多种分布模型，例如高斯分布、洛伦兹分布等。通常，高斯分布是最常用的模型之一，其表达式为：

N(x) = (N_0 / (σ√(2π))) * exp(-(x - x_0)² / (2σ²))

其中：

- `N(x)` 表示在深度`x`处的离子密度
- `N_0` 是表面的最大离子密度
- `x_0` 是最大剂量位置（通常和表面位置相同）
- `σ` 是标准偏差，表示分布的宽窄

### 2.2.2 分布模型的模拟与验证

建立剂量分布模型后，需要通过模拟软件（如Monte Carlo模拟）来验证模型的准确性。模拟过程中会输入初始参数，如离子类型、能量、剂量等，然后进行模拟计算。通过比较模拟结果与实验数据，可以对模型进行优化，以提高剂量计算的精度。

flowchart LR
    A[开始模拟] --> B[输入初始参数]
    B --> C[模拟计算]
    C --> D{模拟结果与实验数据比较}
    D -->|匹配| E[模型验证]
    D -->|不匹配| F[调整模型参数]
    E --> G[结束模拟]
    F --> B

## 2.3 影响剂量精度的因素分析

### 2.3.1 系统误差与随机误差的影响

剂量计算中的误差来源可以分为系统误差和随机误差。系统误差通常来源于设备校准不准确、材料不均匀性等因素，而随机误差则包括了离子束流不稳定性、测量过程中的噪声等。这些因素都会对最终的剂量精度产生影响。

### 2.3.2 实验条件对剂量计算的影响

实验条件如真空度、温度等，同样会影响剂量计算。高真空度可以减少气体分子对离子束的散射作用，而温度的变化则会影响材料的热膨胀系数，进而影响剂量的分布。

| 条件因素 | 影响描述 |
|:---------|:---------|
| 真空度   | 高真空度减少气体散射，提高精度 |
| 温度     | 温度影响材料热膨胀系数，影响剂量分布 |

在进行剂量计算和优化时，需要综合考虑这些因素，并在实验设计阶段就采取相应的措施，以确保最终结果的准确性。

# 3. 离子注入技术实践操作

### 3.1