开源项目分享：贡献和学习MATLAB拟合曲线函数的最佳实践

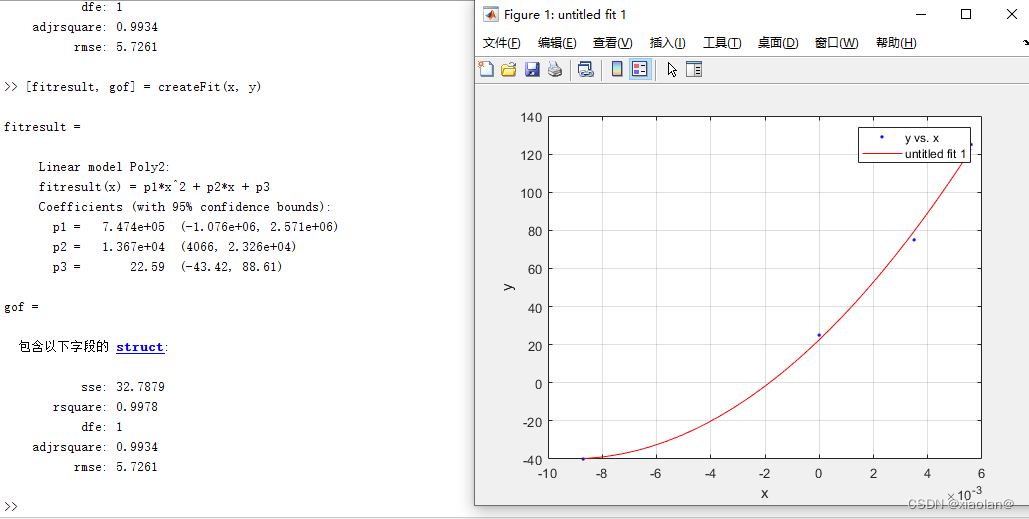
# 1. MATLAB拟合曲线函数简介**

MATLAB拟合曲线函数是一个强大的工具，可以帮助我们从数据中提取有意义的信息。它通过使用数学模型来拟合数据点，从而创建一条曲线，该曲线最能代表数据的趋势。

MATLAB提供了一系列拟合曲线函数，包括线性回归、多项式回归和非线性回归。这些函数可以用来拟合各种类型的数据，从简单的线性关系到复杂的非线性关系。

通过使用MATLAB拟合曲线函数，我们可以获得对数据的深入了解，识别趋势和模式，并进行预测。这在科学、工程和金融等领域有着广泛的应用。

# 2. 拟合曲线函数的理论基础

### 2.1 线性回归

**定义：**

线性回归是一种统计建模技术，用于确定自变量和因变量之间的线性关系。它假设因变量是自变量的线性函数，即：

y = β0 + β1x + ε

其中：

* y 是因变量
* x 是自变量
* β0 是截距
* β1 是斜率
* ε 是误差项

**参数估计：**

线性回归模型的参数可以通过最小二乘法估计，即最小化误差项平方和：

min Σ(y - (β0 + β1x))^2

**拟合优度：**

线性回归模型的拟合优度可以通过决定系数 R^2 来衡量，它表示因变量变异中由自变量解释的比例：

R^2 = 1 - Σ(y - y_hat)^2 / Σ(y - y_bar)^2

其中：

* y_hat 是拟合值
* y_bar 是因变量的平均值

### 2.2 多项式回归

**定义：**

多项式回归是一种线性回归的扩展，它允许自变量与因变量之间存在非线性的关系。多项式回归模型的方程为：

y = β0 + β1x + β2x^2 + ... + βnx^n + ε

其中：

* n 是多项式的阶数

**参数估计：**

多项式回归模型的参数也可以通过最小二乘法估计。然而，随着多项式阶数的增加，模型可能会出现过拟合问题，即模型在训练数据上表现良好，但在新数据上表现不佳。

**正则化：**

为了防止过拟合，可以使用正则化技术，如 L1 正则化或 L2 正则化。正则化通过向损失函数中添加一个惩罚项来限制模型的复杂度。

### 2.3 非线性回归

**定义：**

非线性回归是一种统计建模技术，用于确定自变量和因变量之间非线性的关系。非线性回归模型的方程可以是任意形式，例如：

y = a * exp(bx)

**参数估计：**

非线性回归模型的参数可以通过非线性最小二乘法估计，即最小化误差项平方和：

min Σ(y - f(x, β))^2

其中：

* f(x, β) 是非线性函数

**拟合优度：**

非线性回归模型的拟合优度可以