常见问题解答：解决MATLAB拟合曲线函数的实际应用疑惑

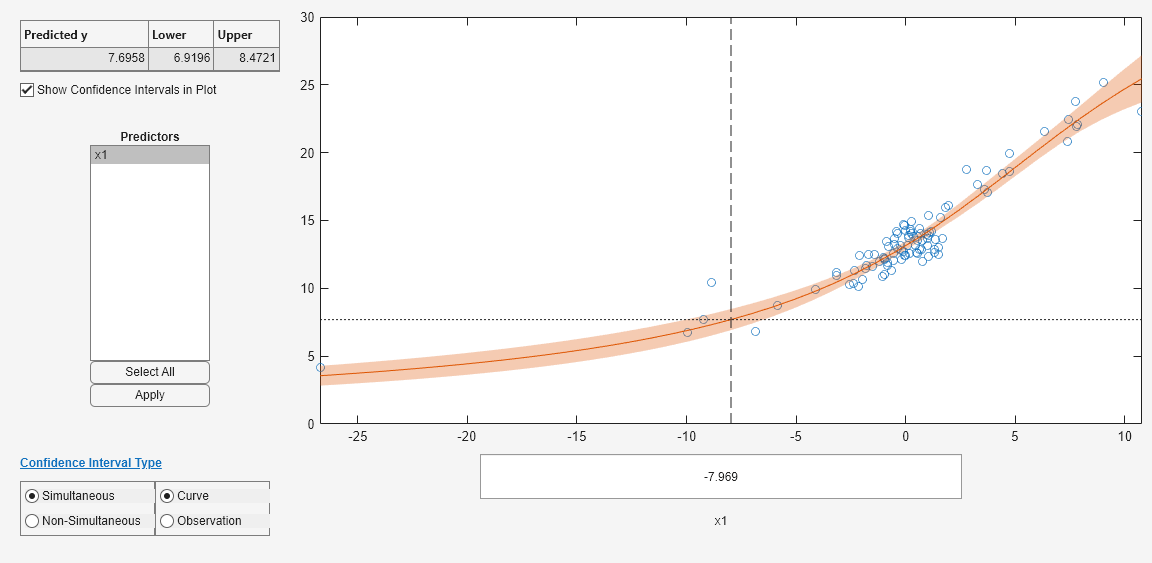
# 1. MATLAB曲线拟合基础**

曲线拟合是利用数学函数来描述数据点之间关系的过程。在MATLAB中，曲线拟合是通过`fit`函数实现的。`fit`函数采用非线性最小二乘法来估计函数参数，以最小化拟合函数与数据点之间的误差。

MATLAB提供了多种曲线拟合函数类型，包括线性函数、多项式函数、指数函数和对数函数。选择合适的函数类型对于获得准确的拟合结果至关重要。

# 2. 曲线拟合函数的类型

### 2.1 线性函数

线性函数是最简单的曲线拟合函数，其形式为：

y = mx + b

其中，`m` 为斜率，`b` 为截距。

**逻辑分析：**

线性函数描述了一条直线，斜率 `m` 表示直线与 x 轴的夹角正切值，截距 `b` 表示直线与 y 轴的交点。

**参数说明：**

* `m`：斜率
* `b`：截距

### 2.2 多项式函数

多项式函数是线性函数的推广，其形式为：

y = a0 + a1x + a2x^2 + ... + anx^n

其中，`a0`、`a1`、`a2`、...、`an` 为多项式的系数。

**逻辑分析：**

多项式函数可以拟合各种形状的曲线，其复杂程度由多项式的次数 `n` 决定。次数越高的多项式，拟合能力越强，但过拟合的风险也越大。

**参数说明：**

* `a0`：常数项
* `a1`：一次项系数
* `a2`：二次项系数
* ...
* `an`：n 次项系数

### 2.3 指数函数

指数函数的形式为：

y = a * e^(bx)

其中，`a` 为底数，`b` 为指数。

**逻辑分析：**

指数函数描述了一条指数曲线，其增长或衰减速率与指数 `b` 成正比。当 `b` 为正时，曲线呈指数增长；当 `b` 为负时，曲线呈指数衰减。

**参数说明：**

* `a`：底数
* `b`：指数

### 2.4 对数函数

对数函数的形式为：

y = log(a, x)

其中，`a` 为底数，`x` 为自变量。

**逻辑分析：**

对数函数描述了一条对数曲线，其增长或衰减速率与对数的底数 `a` 成正比。当 `a` 大于 1 时，曲线呈对数增长；当 `a` 小于 1 时，曲线呈对数衰减。

**参数说明：**

* `a`：底数
* `x`：自变量

**表格：曲线拟合函数类型总结**

| 函数类型 | 形式 | 特点 |
|---|---|---|
| 线性函数 | y = mx + b | 描述直线 |
| 多项式函数 | y = a0 + a1x + a2x^2 + ... + anx^n | 拟合各种形状曲线 |
| 指数函数 | y = a * e^(bx) | 描述指数曲线 |
| 对数函数 | y = log(a, x) | 描述对数曲线 |

# 3. 曲线拟合过程

### 3.1 数据准备

**数据预处理**

在进行曲线拟合之前，需要对原始数据进行预处理，以确保数据的质量和准确性。数据预处理步骤包括：

- **数据清理：**删除缺失值、异常值和噪声数据。
- **数据转换：**根据需要对数据进行转换，例如对数转换或归一化。
- **数据平滑：**使用平滑算法去除数据中的噪声和波动。

### 3.2 模型选择

**模型类型选择**

根据数据的特征和拟合目的，选择合适的曲线拟合函数类型。常见的模型类型包括：

- 线性函数
- 多项式函数
- 指数函数
- 对数函数

### 3.3 参数估计

**参数估计方