工程设计优化新境界：遗传算法在Python中的应用揭秘

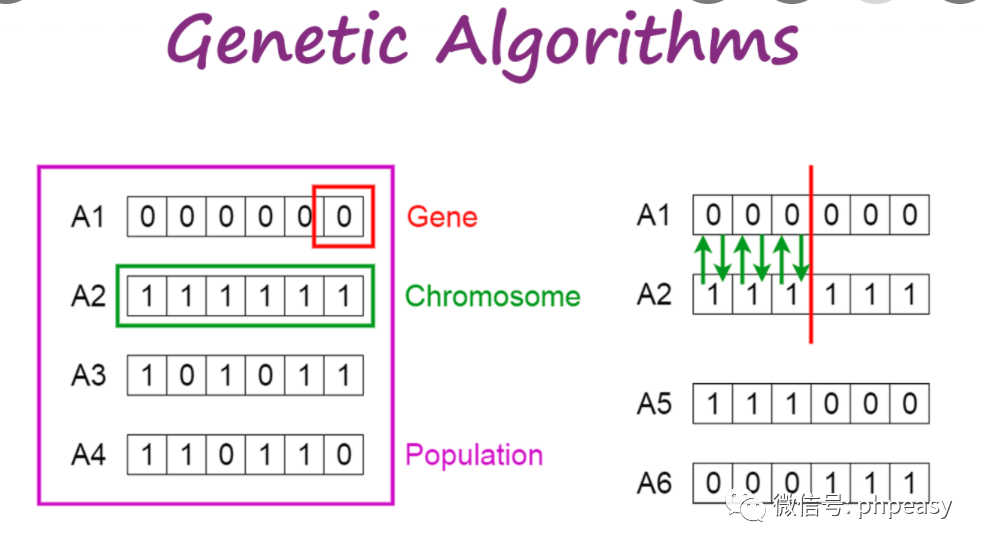
# 1. 遗传算法基础介绍

遗传算法（Genetic Algorithms, GA）是一种模拟自然选择和遗传学机制的搜索优化算法。作为启发式搜索算法，遗传算法依靠随机化搜索的特性，广泛应用于复杂问题的优化中。在这一章，我们将从遗传算法的起源讲起，概述它的基本原理和应用场景，并讨论为何这种算法能够引起众多研究者和工程师的关注。

## 1.1 算法的起源与发展

遗传算法最早由美国学者John Holland及其同事和学生在1970年代提出。Holland的研究意图模仿生物进化中自然选择的过程来解决优化问题。这种算法通过对一组候选解进行选择、交叉（杂交）和变异操作，迭代地产生新一代解，以期找到最优解或近似最优解。

## 1.2 基本原理与概念

遗传算法的核心在于模拟达尔文进化论的基本原理，其主要操作包括：
- **选择（Selection）**：根据适应度函数选出较优个体遗传到下一代。
- **交叉（Crossover）**：通过某种方式交换部分基因，生成新的个体。
- **变异（Mutation）**：随机改变某些个体的基因，以增加种群的多样性。

这些操作共同作用，推动种群不断进化，从而逼近问题的最优解。

## 1.3 应用与意义

遗传算法适用于许多传统优化技术难以解决的复杂问题，如函数优化、调度问题、组合优化等。此外，它在机器学习、人工智能领域也有着广泛的应用。由于遗传算法不需要问题的梯度信息，因此特别适合于非线性、多峰值以及不可微的问题。这一点让它在现实世界的复杂问题中具有独特的优势和重要的应用价值。

# 2. 遗传算法理论详解

### 2.1 遗传算法的核心原理

在本章节中，我们将深入探讨遗传算法的核心原理，并将其与生物学中的进化论进行映射。遗传算法模仿自然选择和遗传机制，通过迭代过程不断进化一个解集。它主要包括以下三个基本操作：选择（Selection）、交叉（Crossover）和变异（Mutation）。我们将逐一分析这些操作，并探讨它们在算法中的实际应用。

#### 2.1.1 进化论在算法中的映射

遗传算法的灵感来源于达尔文的自然选择理论，其中优秀的个体能够适应环境并传承其基因给后代。在算法中，优秀的“个体”通常指那些具有较好解的代表，它们通过“选择”机制被选中，以较高的概率产生后代。交叉操作模拟生物基因的重组，通过交换父代染色体的部分来产生新的后代。变异操作则是在染色体上引入新的遗传变化，增加种群多样性，防止算法早熟收敛。

代码块示例：

# 选择操作：模拟轮盘赌选择机制
def roulette_wheel_selection(population, fitnesses):
    # 计算总适应度与个体适应度所占比例
    total_fitness = sum(fitnesses)
    selection_probs = [f/total_fitness for f in fitnesses]
    # 选择函数
    selected_indices = np.random.choice(range(len(population)), size=len(population), p=selection_probs)
    return [population[i] for i in selected_indices]

# 交叉操作：单点交叉示例
def crossover(parent1, parent2):
    crossover_point = np.random.randint(1, len(parent1)-1)
    child1 = parent1[:crossover_point] + parent2[crossover_point:]
    child2 = parent2[:crossover_point] + parent1[crossover_point:]
    return child1, child2

# 变异操作：随机变异位点
def mutate(individual, mutation_rate):
    for i in range(len(individual)):
        if np.random.rand() < mutation_rate:
            individual[i] = 1 - individual[i]  # 假设染色体为二进制编码
    return individual

### 2.2 遗传算法的数学模型

本节将详细解读遗传算法的数学模型，包括染色体表示与初始化、适应度函数设计以及算法参数的设置与调整。

#### 2.2.1 染色体表示与初始化

在遗传算法中，每个个体通常由一个染色体（Chromosome）表示，这是一串编码了潜在解的符号串。通常，染色体可以被编码为二进制串、实数串或其他适合问题的编码方式。初始化种群时，需要确保种群的多样性，这样算法才有可能探索到问题空间的各个区域。

#### 2.2.2 适应度函数设计

适应度函数（Fitness Function）是评价个体适应环境能力的标准。在遗传算法中，适应度函数直接关联到优化问题的目标函数。设计一个好的适应度函数是算法成功的关键，它需要能够准确反映出个体的解质量。

#### 2.2.3 算法参数的设置与调整

遗传算法中需要设置的参数包括种群大小、交叉率、变异率和选择策略等。这些参数将影响算法的收敛速度和全局搜索能力。参数的选取通常需要通过大量实验和经验进行调整。

### 2.3 遗传算法的优化策略

本节将介绍遗传算法的优化策略，包括群体多样性的维护和高级遗传操作技术。

#### 2.3.1 群体多样性的维护

为了防止早熟收敛，维护种群的多样性至关重要。群体多样性可以通过各种策略来维护，例如适应度分享（Fitness Sharing）、拥挤度算子（Crowding Distance）和多点交叉（Multi-point Crossover）等。

#### 2.3.2 高级遗传操作技术

除了基本的选择、交叉和变异操作外，高级遗传操作技术还包括基因重排（Gene Reordering）、基于优先规则的交叉（Order Crossover）、均匀交叉（Uniform Crossover）等。这些技术可以提高算法的全局搜索能力和问题适应性。

# 3. Python环境下的遗传算法实现

## 3.1 Python编程环境搭建
### 3.1.1 Python基础语法回顾
在深入遗传算法的实现之前，我们首先需要构建一个合适的Python编程环境。Python作为一种解释型编程语言，拥有简洁易读的语法和强大的生态支持，特别适合快速开发算法原型。在开始之前，让我们快速回顾一下Python的基础语法，这对于那些可能需要复习或刚刚接触Python的读者来说是非常有用的。

Python的语法强调可读性和简洁性，使用缩进来表示代码块，而非大括号或其他符号。Python支持多种编程范式，包括面向对象、命令式、函数式和过程式编程。这里我们重点关注与遗传算法实现相关的几个基础概念：

- 变量：Python中的变量无需声明类型，可以直接赋值使用。
- 数据结构：Python提供了丰富的数据结构，如列表（list）、元组（tuple）、字典（dict）和集合（set）等。
- 控制结构：包括条件语句（if-else）和循环语句（for, while）。
- 函数：函数是组织好的，可重复使用的代码块，Python中的函数通过关键字`def`定义。
- 模块：Python中的模块是对Python代码的封装，可以通过import导入其他模块。

### 3.1.2 科学计算库的选择与安装
在Python环境中，强大的科学计算库是实现遗传算法的利器。其中，NumPy和SciPy是两个必备的库。NumPy提供了高性能的多维数组对象，以及相关工具，而SciPy则基于NumPy构建，提供了许多用于科学计算的算法和函数。

为了安装这些库，我们可以使用Python的包管理工具pip。