遗传算法与深度学习的交响曲：打造高效的智能模型

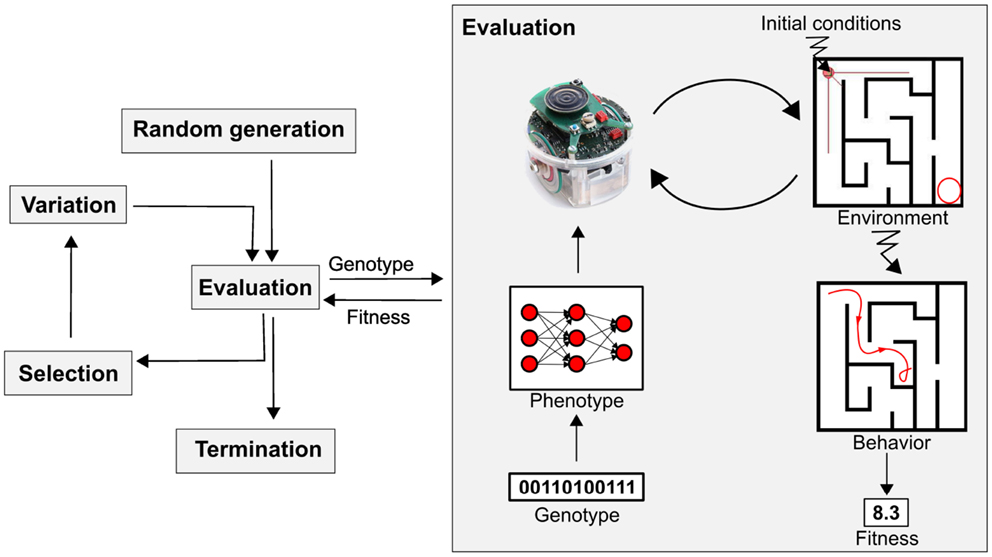
# 1. 遗传算法与深度学习概述

遗传算法与深度学习是当今人工智能领域的两大核心技术，它们各自在处理优化问题和复杂模型学习方面表现出色。本章将对遗传算法和深度学习的基础知识进行初步介绍，并探讨它们之间的关联性和潜在的互补优势。

## 1.1 遗传算法简介

遗传算法是一种模拟自然选择和遗传学原理的搜索优化算法，它通过迭代选择、交叉和变异等操作来优化问题的解决方案。作为一种全局优化算法，它在高维空间和多峰值问题中表现尤为出色。

## 1.2 深度学习概述

深度学习是机器学习的一个分支，主要依靠神经网络结构来学习数据表示。随着计算能力的提升和大数据集的出现，深度学习在图像识别、语音识别、自然语言处理等领域取得了革命性的进步。

## 1.3 遗传算法与深度学习的结合

将遗传算法应用于深度学习模型的参数优化，可以提升模型的性能和效率。本章将深入探讨这两种技术如何相互作用，以及它们在实际问题中的融合方式和应用案例。

通过本章的学习，读者将能够理解遗传算法和深度学习的基础理论，并对它们如何协同工作有一个全面的了解。这将为深入研究后续章节中的具体实现和应用案例打下坚实的基础。

# 2. 遗传算法的理论与实践

## 2.1 遗传算法的基本原理

### 2.1.1 遗传算法的起源与定义

遗传算法（Genetic Algorithm，GA）是一种模拟自然选择和遗传学机制的搜索优化算法。它是由美国计算机科学家John Holland及其同事和学生在20世纪70年代开发的。遗传算法的核心思想是从一个初始种群出发，通过选择（Selection）、交叉（Crossover）和变异（Mutation）等操作，迭代产生新一代种群，使得种群不断进化，最终达到问题的最优解或满意解。

遗传算法作为一种高效的搜索算法，在解决优化问题时具有以下特点：
- **全局搜索能力**：通过种群中的多点搜索，避免了传统优化算法易陷入局部最优解的问题。
- **并行性**：遗传算法在每一代中可以同时评估多个解，易于并行实现。
- **易于实现**：算法不需要问题的特定知识，只要能够定义适应度函数，就能应用遗传算法进行优化。
- **灵活性**：可以通过调整遗传算法的参数和设计特定的交叉、变异操作符来适应特定问题的需求。

### 2.1.2 遗传算法的主要操作：选择、交叉、变异

遗传算法的运行机制可以类比为达尔文的生物进化论，通过选择、交叉和变异三个主要操作来指导种群进化：

**选择（Selection）**：目的是为了让适应环境的个体有更高的机会繁衍后代。在遗传算法中，常用的选择策略有轮盘赌选择、锦标赛选择等，它们保证了适应度高的个体有较大的概率被选中。

graph LR
A[初始种群] -->|选择| B[繁殖池]
B --> C[交叉与变异]
C --> D[生成新一代种群]
D -->|迭代| A

**交叉（Crossover）**：类似于生物遗传中的染色体交叉，交叉操作允许两个个体的部分基因发生交换，以产生新的后代。这个过程增加了种群的多样性，并可能产生更优秀的解。

flowchart LR
A[个体A] -->|交叉| C[新个体]
B[个体B] -->|交叉| C

**变异（Mutation）**：为防止遗传算法过早收敛于局部最优解，变异操作随机改变个体的某些基因，从而在搜索空间中引入新的点。变异可以保持种群的多样性，增加算法探索新解的能力。

flowchart LR
A[个体A] -->|变异| B[新个体]

### 2.2 遗传算法的实现细节

#### 2.2.1 编码与解码机制

在遗传算法中，问题的解需要通过编码转换成染色体（Chromosome）的形式。编码机制的选择取决于问题的性质和需求。常见的编码方式包括二进制编码、实数编码和符号编码。

解码机制则是编码过程的逆过程，它将染色体转换回问题的解空间中的一个可行解。在实现过程中，编码和解码机制的正确性对于遗传算法能否有效搜索最优解至关重要。

flowchart LR
A[问题的解] -->|编码| B[染色体]
B -->|解码| C[恢复的解]

#### 2.2.2 适应度函数的设计

适应度函数是遗传算法中用来衡量个体适应环境能力的函数。设计一个合适的适应度函数是遗传算法成功的关键。适应度函数需要能够准确反映出个体的适应度，以便于进行选择操作。

def fitness_function(individual):
    # 适应度计算逻辑
    pass

在实现中，适应度函数应简洁高效，以确保算法的运行效率。此外，适应度函数的设计需要根据具体问题进行调整，保证能够指导遗传算法向最优解进化。

#### 2.2.3 遗传算法参数的调优

遗传算法的性能很大程度上取决于其参数设置，包括种群大小、交叉率、变异率、选择策略等。这些参数的正确设置对于算法的收敛速度和解的质量具有直接影响。

调优过程通常需要多次实验，通过经验公式初步设定参数值，然后通过实验观察算法的表现进行微调。例如：

params = {
    'population_size': 100,
    'crossover_rate': 0.7,
    'mutation_rate': 0.01,
    'selection_strategy': 'tournament'
}

### 2.3 遗传算法在优化问题中的应用

#### 2.3.1 经典优化问题的遗传算法解决方案

遗传算法在解决经典的优化问题，如旅行商问题（TSP）、作业调度问题（JSP）和背包问题（KP）等，表现出了良好的性能。它能够处理这些NP-hard问题的复杂搜索空间，并找到可接受的近似解。

例如，在解决TSP问题时，遗传算法通过编码路径为染色体，交叉和变异操作被设计为路径片段交换，以维护路径的有效性。适应度函数设计为路径长度的倒数，目标是优化路径的总长度。

#### 2.3.2 遗传算法与其他优化算法的比较

与其他优化算法如梯度下降法、模拟退火和蚁群算法等相比，遗传算法具有其独特的优势和局限。例如，梯度下降法在优化连续可微函数时非常有效，但它不适合于离散或非凸优化问题。而遗传算法通过模拟自然进化的过程，可以有效地探索这类问题的解空间。

在实际应用中，选择哪种优化算法取决于问题的特性、解空间的复杂性和对解质量的要求。有时，结合多种算法的优点，形成混合优化策略，会获得更好的优化效果。

| 优化算法       | 优点                                           | 缺点                                         |
| -------------- | ---------------------------------------------- |