揭秘Origin：线性拟合参数设置与应用的完全解析


参考资源链接：[Origin中线性拟合参数详解：截距、斜率与相关分析](https://wenku.csdn.net/doc/6m9qtgz3vd?spm=1055.2635.3001.10343)
# 1. 线性拟合的数学基础与理论

## 1.1 线性关系的基本概念

在科学研究和工程技术领域，线性关系是最基本且常见的数学模型之一。它描述了两个变量之间的线性相关性，即一个变量是另一个变量的线性函数。数学上，这种关系可以用方程式 y = mx + b 来表达，其中 m 表示斜率，b 表示截距。线性拟合的目的在于找到最佳的 m 和 b，使得所有观测数据与线性模型的偏差之和最小化。

## 1.2 最小二乘法

最小二乘法是实现线性拟合的核心算法。通过最小化误差的平方和，该方法可以找到一条最接近所有数据点的直线。在数学上，这涉及到对 m 和 b 进行优化计算，以使拟合线与实际数据点之间的垂直距离平方和达到最小。该方法能有效处理数据中的随机误差，并且适用于大多数线性回归模型的求解。

## 1.3 线性回归分析

线性回归分析不仅限于单一变量的线性关系，也可以扩展到多元线性回归，处理两个或更多自变量与一个因变量之间的线性关系。在这种情况下，最小二乘法需要适应到多变量情况，使用线性代数中的矩阵运算来求解参数。通过这一分析，我们可以更深入地理解变量之间的相互影响，以及预测新数据点的可能结果。

# 2. ```
# 第二章：Origin软件简介及其线性拟合功能

## 2.1 Origin软件概述
Origin是一款广泛使用的科学绘图和数据分析软件，由OriginLab公司开发。它提供了丰富的工具来进行数据处理和可视化，特别适合于科研人员和工程师分析实验数据。Origin提供了强大的数据导入、处理、绘图和拟合功能，深受学术界和工业界的青睐。Origin的界面采用图形用户界面（GUI），使得非编程背景的用户也能快速上手。

### Origin软件的特点
- 多种数据输入方式，包括Excel数据表、文本文件等。
- 强大的数据处理工具，包括数据筛选、统计分析、插值、FFT等。
- 丰富的二维和三维图形模板，能够生成高质量的出版级图表。
- 提供了Origin C以及LabTalk脚本语言，方便用户编写自定义函数和批量处理数据。
- 集成线性拟合、非线性拟合和多变量分析等多种统计和拟合工具。

## 2.2 Origin的线性拟合功能
Origin软件中的线性拟合功能是数据分析的核心功能之一。通过线性拟合，用户可以快速地将实验数据点拟合成一条直线，并从中获取重要的物理参数，如斜率和截距。Origin中的线性拟合工具，不仅可以拟合简单的直线方程，还支持复杂模型的定制和拟合。

### 线性拟合的基本步骤
1. 数据准备：首先需要在Origin中准备数据，数据通常是成对的X和Y值，可以通过导入Excel文件或者手动输入。
2. 选择拟合工具：在Origin的菜单栏中选择“分析” -> “拟合” -> “线性拟合”，打开线性拟合对话框。
3. 设置拟合参数：在弹出的对话框中可以设置拟合范围、权重、误差处理方式等参数。
4. 拟合操作：设置完毕后，执行拟合操作，Origin会显示拟合结果的图形以及详细的拟合参数。
5. 结果分析：对拟合结果进行分析，包括斜率、截距、R平方值等统计信息。

### Origin中的线性拟合界面操作
Origin的线性拟合界面非常直观，提供了多种参数设置选项，使得用户可以对拟合过程和结果进行精细控制。

- 在线性拟合对话框中，可以勾选“显示拟合方程”，Origin会自动在图形上显示拟合方程和相关统计参数。
- 用户可以通过“选项”按钮设置拟合选项，例如是否显示误差栏、数据点的样式等。
- 通过“输出”按钮，用户可以将拟合结果输出到工作表或报告表中。

### 线性拟合结果与统计信息
拟合完成后，Origin会在图形窗口中展示拟合曲线，并在报告表中提供详细的统计结果。以下是一些关键的统计信息：

- 斜率（Slope）：直线的斜率代表了X和Y之间的关系强度，斜率的正负也表明了X和Y的相关性方向。
- 截距（Intercept）：直线与Y轴的交点，提供了拟合直线的起始值信息。
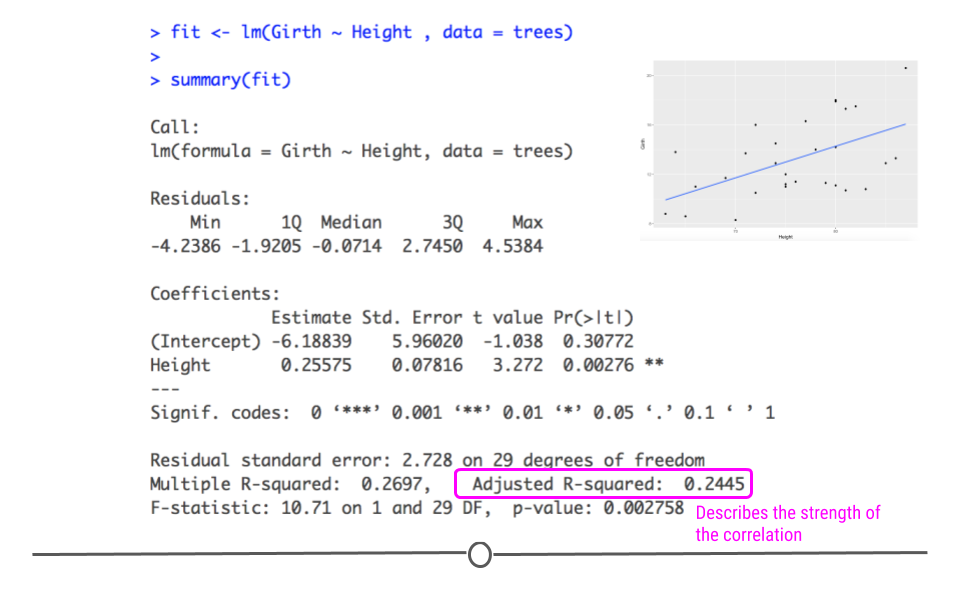
- R平方值（R-Square）：表示拟合直线与数据点的吻合程度，R平方值越接近1，表明拟合效果越好。
- 标准偏差（Standard Error）：表示拟合参数的不确定性，越小的标准偏差表明拟合参数越可靠。

## 2.3 Origin线性拟合与数据可视化
Origin不仅提供了强大的线性拟合功能，还能够将拟合结果与原始数据一起展示，增强了数据的可视化效果。用户可以自定义图形的各种元素，如颜色、线型、标签等，以满足不同的展示需求。

### 线性拟合图形的操作
- 在拟合结果图形中，可以通过右键点击图层来调整图形的属性，比如坐标轴的范围和刻度。
- 用户可以添加数据标记、误差条或数据表到图形中，方便对数据点进行更详细的分析。
- Origin还允许用户将多个图形组合在一个页面上，便于对多个数据集进行比较分析。

### 结合数据图表使用线性拟合
- 结合误差线图：在某些实验中，数据点带有误差，用户可以在Origin中使用带有误差线的散点图来更精确地展示数据。
- 结合箱线图：箱线图可以展示数据的分布情况，与线性拟合结果结合后，能够直观反映数据分布与拟合线的关系。
- 结合多面板图：在处理多个数据集时，可以使用多面板图将每个数据集的线性拟合结果并排展示，便于分析比较。

## 2.4 Origin的线性拟合实践案例
为了进一步理解Origin中线性拟合的功能，以下是一个简单的实践案例，通过该案例可以掌握Origin的基本操作以及线性拟合的过程。

### 实践案例：分析某组实验数据
假设我们有一组实验数据，记录了温度（X轴）和电阻值（Y轴）之间的关系。我们想要通过线性拟合来确定电阻值随温度变化的趋势。

1. 导入数据：首先将含有温度和电阻值的Excel文件导入Origin中，创建一个新的工作表。
2. 选择拟合工具：点击菜单栏的“分析” -> “拟合” -> “线性拟合”。
3. 设置拟合选项：在打开的对话框中，指定X和Y的列，调整拟合范围，勾选需要显示的统计信息。
4. 执行拟合：点击“确定”，Origin会自动拟合数据并显示图形和结果。
5. 分析结果：查看拟合直线的斜率和截距，分析其物理意义。斜率可能表示了电阻随温度变化的敏感度，而截距可能是常温下的电阻值。

通过这个实践案例，可以看出Origin的线性拟合不仅直观，而且操作简便，即便是初学者也能快速掌握基本的拟合操作。

总结而言，Origin软件提供了全面的线性拟合工具和灵活的数据可视化选项，是科研人员进行数据分析的得力助手。通过本节的学习，您应该对Origin的线性拟合功能有了初步的了解，并能够开始尝试使用Origin来分析您的实验数据。

# 3. 线性拟合参数的设置与优化

## 3.1 Origin中的线性拟合参数介绍

### 3.1.1 斜率与截距的设置

在进行线性拟合时，斜率（slope）和截距（intercept）是两个基本且重要的参数。它们定义了拟合直线的形态和位置。在Origin中设置这两个参数的步骤如下：

1. 打开Origin软件，并导入需要进行线性拟合的数据集。
2. 选中数据列，使用快捷键 `Ctrl+Y` 或点击工具栏上的“线性拟合”图标来打开拟合对话框。
3. 在拟合对话框中，可以找到“线性拟合”选项卡，勾选“显示公式”，在公式中即可看到斜率（slope）和截距（intercept）。
4. 斜率和截距的数值默认为自动计算得出，用户也可以手动输入特定的值来进行拟合。

例如，如果在拟合对话框中设定斜率和截距，Origin会使用这些值来拟合数据。这在你对数据集有特定先验知识时非常有用。

### 3.1.2 数据权重与误差分析

在科学测量中，数据点的可靠性可能会因测量方法和仪器精度的不同而存在差异。为了反映这种差异，Origin允许用户为数据点赋予不同的权重，并进行误差分析。在进行数据权重设置时，可以考虑以下几种方式：

- 无权重（Uniform Weights）：所有数据点具有相同的权重。
- 1/σ^2 权重（Inverse Variance）：每个数据点的权重与其测量误差的平方成反比。
- 可变权重（Variable Weights）：用户可以自定义每个数据点的权重。

误差分析是确定数据可靠性的重要手段。Origin支持使用不同误差模式进行拟合，包括：

- 常数相对误差（Constant %）。
- 常数绝对误差（Constant）。
- Y值的误差（Y Error）。

### 3.1.3 拟合策略与收敛条件

拟合策略指的是Origin在拟合过程中采用的方法，它包括线性最小二乘法、非线性最小二乘法等。Origin允许用户选择适当的拟合策略以获得最佳结果。

收敛条件则决定了拟合算法何时停止迭代。主要包括以下参数：

- 最大迭代次数（Max Iterations）：设置算法运行的最大迭代次数。
- 收敛标准（Tolerance）：当拟合结果的改变量小于给定容忍度时，认为算法已收敛。
- 参数变化容忍度（Parameter Tolerance）：用于控制参数更新的步长。

理解并合理设置这些参数对于获得可靠和准确的拟合结果至关重要。不当的设置可能会导致拟合算法不收敛或者收敛到局部最优解。

## 3.2 拟合效果的评价指标

### 3.2.1 卡方检验和R平方值

为了评价拟合模型的有效性，常用的指标包括卡方检验和R平方值。卡方检验可以评估数据点与拟合模型之间的偏差。在Origin中，可以通过执行拟合后，查看报告表中的卡方值来分析拟合优度。

R平方值是一个统计量，用于衡量模型对数据变异性的解释程度。在理想情况下，R平方值越接近1，表明模型拟合度越高。拟合报告中也会包含R平方值，可以帮助用户评估拟合的效果。

### 3.2.2 残差分析与异常点检测

残差分析是指检查拟合直线与数据点之间差异的方法，它是拟合优度分析的重要组成部分。在Origin中，可以创建残差图来观察残差的分布情况。

异常点，也称为离群点，是拟合过程中值得注意的数据点，它们可能会对拟合结果产生较大影响。Origin提供了多种方法来检测和处理异常点，例如使用标准残差来识别并分析这些点。

## 3.3 拟合过程的优化技巧

### 3.3.1 初始值的合理设定

初始值是拟合算法开始迭代的起点，合理设定初始值可以加速拟合算法的收敛，避免陷入局部最优解。在Origin中，用户可以手动设定初始值，也可以让软件根据数据自动估计初始值。

### 3.3.2 多参数拟合的策略调整

对于具有多个参数的复杂模型，拟合过程会更加复杂。Origin提供了多种策略来处理多参数拟合问题：

- 连续拟合（Sequential Fit）：依次对每个参数进行拟合。
- 全局拟合（Global Fit）：同时对所有参数进行拟合。
- 单一拟合（Single Fit）：对整个数据集使用单一模型进行拟合。

适当的策略选择依赖于数据特性和用户的研究目标，选择合适的策略可以有效提高拟合效果。


在本章中，我们详细介绍了Origin软件中线性拟合参数的设置与优化方法。接下来，我们将探讨如何通过拟合效果的评价指标来判断拟合质量，并介绍在拟合过程中优化技巧的实践应用。这些方法共同构成了线性拟合中不可或缺的一部分，为科学研究提供强有力的数据分析工具。

# 4. 线性拟合在各领域的应用案例

## 4.1 物理学中的应用

### 4.1.1 直线运动与加速度测量

在物理学领域，线性拟合被广泛应用于直线运动的数据分析，尤其是加速度的计算。当物体进行直线运动时，其位移与时间的关系往往可以用一条直线来表示，该直线的斜率即为加速度。利用Origin软件，研究人员可以轻松地对实验数据进行线性拟合，以求得物体的加速度。

例如，在自由落体实验中，记录物体从一定高度自由落下的时间与位移数据。通过Origin进行线性拟合后，斜率便可表示为加速度g，这不仅验证了重力加速度的理论值，还可以揭示实验误差或真实物理过程中的细微差别。

# 示例代码块 - 使用Origin进行线性拟合计算加速度
# 假设数据集包括时间点（t）和位移（s）两列数据
# 在Origin中使用线性拟合工具，选择"Analysis" -> "Fitting" -> "Linear Fit"
# 将位移数据（s）作为Y值，时间数据（t）作为X值进行拟合

# Origin中进行线性拟合的命令示例（需在Origin软件的脚本编辑器中执行）
linearFit -o FitLinear1 [Book1]sheet1!1:2

### 4.1.2 电阻定律与电路分析

欧姆定律描述了电阻、电流和电压之间的线性关系，这为电路分析提供了理论基础。在实际应用中，通过测量不同电压下的电流值，可以使用线性拟合来确定电路的电阻值。

例如，对一个电阻进行多次测量，记录不同的电压值与对应的电流值。通过Origin软件进行线性拟合，可以得到一条拟合直线，其斜率即为电阻的倒数（1/R），从而可以计算出电阻R的准确值。

## 4.2 工程技术中的应用

### 4.2.1 材料强度与应力分析

在材料科学与工程领域，线性拟合是研究材料强度与应力关系的重要工具。通过施加不同大小的力于材料上并记录应变，可以得到应力-应变曲线。当材料处于弹性范围内时，这种关系往往是线性的。

例如，在金属拉伸测试中，拉力（F）与伸长量（ΔL）之间的关系可以通过线性拟合获得弹性模量（E），即拉力与横截面积（A）和伸长量与原长（L）之比的比值。

# 示例代码块 - 使用Origin进行弹性模量的线性拟合计算
# 假设数据集包括拉力（F）和伸长量（ΔL）两列数据
# 在Origin中使用线性拟合工具，选择"Analysis" -> "Fitting" -> "Linear Fit"
# 将伸长量数据（ΔL）作为Y值，拉力数据（F）作为X值进行拟合

# Origin中进行线性拟合的命令示例（需在Origin软件的脚本编辑器中执行）
linearFit -o FitLinear2 [Book2]sheet1!1:2

### 4.2.2 信号处理与系统识别

在信号处理和系统识别领域，线性拟合常被用于分析系统对输入信号的响应。一个典型的例子是识别线性时不变（LTI）系统的冲激响应。通过对系统输入信号和输出信号的离散数据进行线性拟合，可以辨识系统的传递函数。

例如，系统输入信号（x）与输出信号（y）之间的关系可以通过线性拟合表达为y = H(x)，其中H表示系统的冲激响应。通过Origin软件分析，可以得到系统的频率响应特性，进而进行滤波器设计、信号去噪等应用。

## 4.3 生物科学中的应用

### 4.3.1 生化反应速率分析

在生物化学研究中，线性拟合常常用于分析酶促反应的速率。通过记录不同底物浓度下反应速率的变化，可以绘制出米氏方程（Michaelis-Menten equation）曲线。

当底物浓度较低时，反应速率随底物浓度的增加而线性增加，此时可以使用线性拟合来估算最大反应速率（Vmax）和米氏常数（Km），对于理解和优化酶促反应具有重要意义。

### 4.3.2 遗传学中的基因表达拟合

在遗传学研究中，线性拟合是分析基因表达数据的常用工具。基因表达水平与实验条件之间的关系往往通过微阵列或RNA测序技术得到一系列数据点。这些数据点在一定范围内可以近似为线性关系，从而可以通过线性拟合分析来确定基因表达的动态变化。

例如，在研究特定基因在不同时间点的表达水平时，将时间作为X轴，相对表达量作为Y轴，通过线性拟合可以揭示基因表达随时间的变化趋势和速率。

# 示例代码块 - 使用Origin进行基因表达数据的线性拟合分析
# 假设数据集包括时间点（time）和基因表达量（expression）两列数据
# 在Origin中使用线性拟合工具，选择"Analysis" -> "Fitting" -> "Linear Fit"
# 将基因表达量数据（expression）作为Y值，时间数据（time）作为X值进行拟合

# Origin中进行线性拟合的命令示例（需在Origin软件的脚本编辑器中执行）
linearFit -o FitLinear3 [Book3]sheet1!1:2

在以上各应用案例中，线性拟合作为分析工具的核心价值在于其简化和直观性，通过线性模型的建立，能快速分析出数据间的关系并揭示背后的现象。随着科学技术的发展，线性拟合在各个领域都发挥着不可替代的作用，为科研工作提供强有力的支撑。

# 5. Origin线性拟合高级技巧与展望

## 5.1 自定义函数拟合

### 5.1.1 编写自定义模型

在Origin中，自定义函数拟合是通过使用内置的公式语言来实现的，这样可以对标准线性拟合模型进行扩展。比如，我们可能会遇到一些非线性数据，这时候就需要利用Origin提供的公式编辑器来创建一个新的拟合函数。

举个例子，假设我们有一组数据，它遵循指数衰减的规律，我们就可以编写一个自定义的拟合函数来描述这种行为：

f(x) = A*exp(-x/t) + C

在这个公式中，`A` 表示初始值，`t` 为时间常数，`C` 表示基线值。编写完毕后，就可以将其应用到数据上进行拟合了。

### 5.1.2 复杂数据集的拟合分析

对于复杂的数据集，有时需要构建多变量或多个参数的模型，以更准确地拟合数据。例如，在化学反应速率的研究中，可能需要同时考虑温度和压力的影响。Origin 允许用户通过添加多个独立变量来构建复杂的函数模型，进行多参数拟合。

在构建这些模型时，重要的是要理解各个参数的物理或化学意义，并根据先验知识或实验设计来合理地设置参数的初始值。此外，还可以利用Origin提供的拟合诊断工具，比如残差分析、参数的置信区间估计等，来提高模型的适用性和预测精度。

## 5.2 线性拟合结果的自动化处理

### 5.2.1 批量处理与脚本控制

Origin提供了强大的脚本语言，即LabTalk，允许用户编写脚本来自动化重复性的数据处理和拟合任务。通过LabTalk脚本，可以实现数据的批量导入、预处理、拟合，以及结果的自动提取和存储。

例如，如果要对一个包含多个文件的数据集进行批量拟合，可以编写一个脚本循环处理每一个文件，并保存拟合结果到指定的工作表或文件中。以下是一个简化的脚本示例：

// 循环处理工作表中的数据文件
loop(ii, 1, 10)
{
// 假设数据文件以 ii 变量命名
string fname$ = "data_$(ii).dat";
impasc fname$;
// 执行线性拟合
linfit x y:=col(2);
// 提取并保存拟合结果到工作表
%A[Result] = %(col(3)_name$);
%B[Result] = %(col(4)_name$);
// 清除当前工作表准备下一轮拟合
newsheet;
}

### 5.2.2 结果的图形化展示与导出

拟合完成后，将结果进行可视化展示是非常重要的一步。Origin提供了多种图形展示方式，包括二维散点图、线图和误差线图等。用户可以根据数据的特点和需求选择合适的图表类型，直观地展示拟合过程和结果。

在Origin中，可以利用内置的图形模板快速地生成专业级的图表。此外，用户还可以自定义图表的样式、颜色和标注，以及将图表导出为常见的文件格式，如图片、PDF或SVG等，方便在论文、报告中使用。

## 5.3 未来发展趋势与展望

### 5.3.1 多变量拟合与人工智能

随着科技的发展，多变量拟合和人工智能技术在数据处理领域中的作用日益显著。多变量拟合能够解决更加复杂的科学问题，其中涉及的变量和参数数量都远多于传统的线性拟合。未来的Origin软件可能将集成更多机器学习算法，以便于处理和分析这类复杂问题。

人工智能的引入将使拟合过程更加智能，如自动识别数据中的模式和趋势，优化拟合模型和参数选择等。这将大幅提高拟合的准确性和效率，特别是在对拟合结果有着严格要求的生物科学、材料科学等领域。

### 5.3.2 云平台与协作分析

云计算技术的普及为数据处理和分析带来了新的可能性。通过将Origin软件与云平台结合，用户可以在任何地点、任何时间访问和分析数据，实现团队之间的实时协作。未来的Origin可能提供这样的云平台服务，使得数据共享和远程分析变得简单便捷。

此外，云平台可以提供更强大的计算资源和存储空间，对于处理大规模的数据集，或是运行复杂的多变量拟合模型，都有着不可替代的优势。用户还可以利用云平台进行数据备份、版本控制和结果共享，进一步提高科研工作的效率和质量。