【数据拟合与分析】：曲线拟合技术，Origin专家教程


# 摘要
本文旨在全面概述曲线拟合技术的基础知识和应用实践，以助于理解和掌握数据拟合的复杂性。首先，文章介绍了曲线拟合的基本概念、理论基础和评价标准。随后，通过Origin软件的实际应用案例，讲解了该软件在数据导入、基本和高级拟合操作中的具体使用技巧。文章还探讨了曲线拟合在实验数据处理、工程问题解决以及科学研究中的应用，并深入研究了多变量数据拟合、非线性模型参数估计及复杂数据集拟合策略等进阶技术。最后，本文阐述了Origin软件的扩展应用与技巧，如自定义脚本、与其他数据处理软件的交互以及社区支持和学习资源，为曲线拟合提供了一套全面的分析工具和学习路径。

# 关键字
曲线拟合；数据拟合；最小二乘法；拟合优度；Origin软件；多变量分析

参考资源链接：[Origin8.5谱线分析指南：单峰拟合步骤解析](https://wenku.csdn.net/doc/459u3yzkp3?spm=1055.2635.3001.10343)
# 1. 数据拟合基础与曲线拟合技术概述

在当今的科研和工程实践中，数据拟合是一种必不可少的工具，用于从一系列数据点中发现潜在的模式或关系。在这一章中，我们将介绍数据拟合的基本概念，以及曲线拟合技术在不同领域的应用。拟合的过程通常涉及选择一个模型，它可以是线性的或非线性的，并使用一系列观测数据来确定模型的参数。本章将涵盖以下主题：

- 数据拟合与曲线拟合的区别和联系。
- 数据拟合在科学研究和工业应用中的重要性。
- 为初学者和专业人员概述曲线拟合流程中的关键步骤。

在后续章节中，我们将深入探讨曲线拟合的理论基础，包括最小二乘法、拟合优度的评价标准，以及使用专业的软件工具进行实际操作的详细步骤。数据拟合技术是理解复杂数据集的重要手段，掌握这些方法可以极大地增强您的数据分析能力。

# 2. 曲线拟合的理论基础

## 2.1 数学模型与拟合原理
### 2.1.1 拟合模型的数学描述
在曲线拟合的过程中，拟合模型的数学描述是核心要素，它决定了数据点将如何被逼近一条或多条曲线。通常，拟合模型可以描述为一组函数关系式：

\[y_i = f(x_i;\theta) + \epsilon_i\]

其中，\(y_i\) 表示测量值或实验数据点，\(x_i\) 是自变量数据点，\(f\) 代表拟合函数，\(\theta\) 是函数参数，而 \(\epsilon_i\) 代表误差项。拟合的目标是找到一组参数 \(\theta\)，使得误差项 \(\epsilon_i\) 的某种度量最小化。

### 2.1.2 最小二乘法的理论基础
最小二乘法是一种标准的优化技术，广泛用于曲线拟合，其目的是减少误差的平方和。在最简单的线性回归情况下，最小二乘法可以表示为求解下面的目标函数：

\[S(\theta) = \sum_{i=1}^{n} (y_i - f(x_i;\theta))^2\]

通过调整 \(\theta\)，求解目标函数的最小值，可以得到最佳拟合曲线。对于非线性模型，求解过程可能需要迭代方法如牛顿法或梯度下降法。

## 2.2 曲线拟合方法的分类
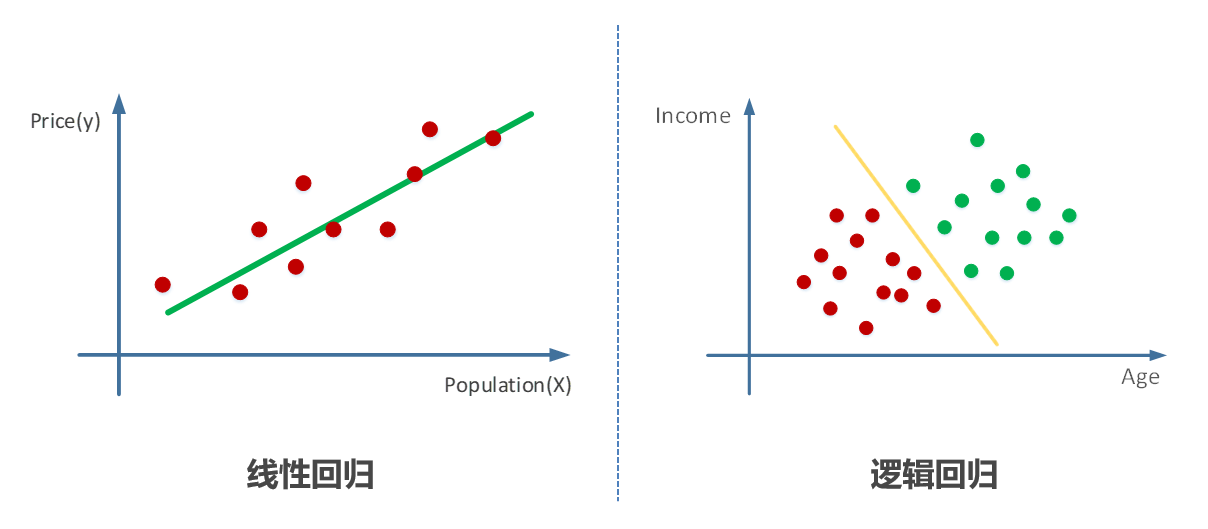
### 2.2.1 线性回归与非线性回归
在曲线拟合中，线性回归和非线性回归是最基本的拟合方法。线性回归假设数据点与自变量之间存在线性关系，模型可以表示为：

\[y = \beta_0 + \beta_1x + \epsilon\]

而非线性回归的模型则更为复杂，例如指数函数或对数函数拟合，模型可以表示为：

\[y = \beta_0 \exp(\beta_1x) + \epsilon\]

### 2.2.2 多项式拟合与指数/对数拟合
多项式拟合是通过构建一个多项式函数来逼近数据点，模型通常表示为：

\[y = \beta_0 + \beta_1x + \beta_2x^2 + ... + \beta_nx^n + \epsilon\]

指数拟合与对数拟合是处理数据呈指数或对数关系的场景，例如，指数拟合模型可能为：

\[y = \beta_0 \exp(\beta_1x) + \epsilon\]

或对数拟合模型为：

\[y = \beta_0 + \beta_1 \ln(x) + \epsilon\]

## 2.3 拟合优度的评价标准
### 2.3.1 残差分析与R平方值
拟合优度的评价标准之一是残差分析。残差是每个数据点与其在拟合曲线上的对应点之间的差值。理想的拟合模型应具有小的残差值。R平方值（决定系数），是评价拟合好坏的统计量，它表示拟合模型解释的变异性比例，计算公式为：

\[R^2 = 1 - \frac{\sum_{i=1}^{n} (y_i - \hat{y_i})^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2}\]

其中，\(\hat{y_i}\) 是拟合值，\(\bar{y}\) 是响应变量的均值。

### 2.3.2 F检验和t检验在拟合中的应用
F检验用于比较两个模型的拟合优度，通常用于检验整个模型的有效性，其基本思想是比较模型的平均误差平方和与剩余误差平方和。t检验则用于检验回归系数是否显著异于零，即模型中某个自变量是否对响应变量有显著影响。

| 应用场景 | F检验 | t检验 |
| --------- | ------ | ------ |
| 模型整体评价 | 适用 | 不适用 |
| 自变量重要性评价 | 不适用 | 适用 |

在实际应用中，通常需要结合R平方值、F检验和t检验等多个指标，全面评价拟合模型的质量。

graph LR
A[开始拟合分析] --> B[构建初始模型]
B --> C[计算残差]
C --> D[计算R平方值]
D --> E[进行F检验]
E --> F[进行t检验]
F --> G[评价拟合优度]

在上述流程图中，展示了从构建初始模型到评价拟合优度的完整分析流程，每一个步骤都至关重要。在实际操作中，可能需要多次迭代优化模型，才能获得最佳拟合效果。

# 3. Origin软件在曲线拟合中的应用

## 3.1 Origin界面与数据导入导出

### 3.1.1 Origin的用户界面介绍

Origin是一款流行的科学绘图和数据分析软件，广泛应用于科学和工程领域。它的用户界面设计直观，通过一个集成的图形窗口为用户提供数据操作、图形绘制和分析功能。界面主要由菜单栏、工具栏、工作表（Worksheet）、图形窗口和布局窗口组成。

- **菜单栏**提供了完整的操作指令，包括数据导入、数据处理、图形生成、分析工具和导出等。
- **工具栏**提供快速访问最常用命令的按钮，便于用户快速操作。
- **工作表**是Origin的核心，用于输入、查看和编辑数据。
- **图形窗口**显示绘制的图表和图形。
- **布局窗口**允许用户组织多个图形和文字，用于报告和演示。

### 3.1.2 数据导入导出的方法与技巧

在使用Origin进行数据分析之前，首先需要将数据导入到软件中。Origin支持多种数据格式的导入导出，常见的数据格式如Excel、Text/CSV、MATLAB、Databases等都可以无缝导入。

- **Excel数据导入**：可以直接打开Excel文件或者复制粘贴数据到工作表中。
- **文本文件导入**：Origin提供了强大的文本导入向导，可以对不同格式的文本文件进行解析，并转换为表格数据。
- **导出数据**：Origin支持导出为多种格式，包括常见的图像格式（如PNG、JPG）、PDF，以及矢量图形格式（如SVG、EPS），还有数据文件格式（如Excel、Text等）。

在导入数据时，要注意正确设置列类型（如数值、文本、日期等），以便后续分析。导出数据时，要选择适当的导出格式以满足不同的需求，例如高质量的图像格式用于出版或矢量图形格式用于学术报告。

## 3.2 利用Origin进行基本拟合操作

### 3.2.1 创建二维和三维拟合图形

Origin软件中创建二维和三维拟合图形是非常直接的。首先，将数据导入工作表，然后通过菜单栏选择“分析”（Analyze），找到“拟合”（Fit）子菜单，选择合适的拟合模型进行操作。

- **二维拟合图形**：在二维平面上，Origin能够生成散点图（Scatter Plot）、线图（Line Plot）、条形图（Bar Plot）等，并且可以对图形进行多种拟合操作。用户可以通过“绘图”（Plot）菜单选择“新建图形”（New Graph）进行创建。
- **三维拟合图形**：对于三维数据集，Origin提供三维散点图、三维曲面图等。用户可以通过选择“绘图”菜单中的“新建三维图形”（New 3D Graph）选项进行创建，并通过“分析”菜单进行三维数据的拟合操作。

### 3.2.2 配置拟合参数与初始条件

在进行拟合之前，用户需要配置拟合参数和初始条件以获得最佳的拟合结果。Origin允许用户在图形界面中直接设置拟合参数，也可以通过编写拟合函数来控制拟合过程。

- **拟合函数编辑器**：通过“分析”菜单进入“拟合函数编辑器”（Fit Function Organizer），用户可以编辑或创建新的拟合函数，并设置初始参数值。
- **拟合控制面板**：在图形窗口，用户可以打开拟合控制面板来调整拟合参数，如选择不同的拟合算法、设置参数上下限、激活或禁用特定参数等。

配置参数时，重要的是要理解每个参数代表的意义，并根据数据的特点进行合理设定。初